Действия над непрерывными функциями. Свойства непрерывных функций. Точки разрыва непрерывных функций

Общие свойства непрерывных функций, заданных в промежутке [а, b], определяются четырьмя теоремами: двумя теоремами Больцано— Коши и двумя теоремами Вейерштрасса.

первая теорема Больцано-Коши. Пусть функция f{x) определена и непрерывна в [a, b ]. Тогда, если f(a)* f(b) < 0, то (а, Ь): т = 0.

Доказательство. Пусть, для определенности, f (a) < 0 uf{b) > 0. Обозначим [a, b ] как [ a, b ] и разделим его пополам. Тогда в точке a₀+b₀/2 либо f(х) обратится в нуль, и теорема будет доказана, либо на одной из половин отрезка знаки функции в концевых точках останутся различными. Выберем эту половину и обозначим ее [a₁, b₁]. Далее про­должим процесс деления [a₁, b₁] пополам. В точке a₁+b₁/2 либо получим нулевое значение f(х), либо на одной из половин[a₁, b₁] функция будет иметь разные знаки на концах. В первом случае теорема подтвердится, во втором - образуется новый отрезок, который обозначим [а₂, b₂]. В дальнейшем данная процедура либо прервется, если на одной из середин делимых отрезков получим нулевое значение f(х), либо образуется бесконечная последовательность вложенных промежутков [а_n, b_n] длиной l_n = b_n – a_n = l₀/2ⁿ= b₀ – a₀/2ⁿ

При возрастании п длина l­_n --> 0 и по лемме Кантора точки а_n и b_n образуют две сходящиеся к общему пределу последовательности: 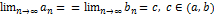, тк и

В соответствии с выбором при n f(а_п) < 0 и f(b_п) > 0, поэтому

C другой стороны, в точке с и

Поэтому f(c)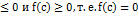

вторая теорема Больцано—Коши. Пусть функция f(х) определена и непрерывна в [а, b]. Тогда, если f(а)≠ f(b), то при М), где т = min {f(a), f{b)}, М = max {f(a), f(b)}, (а, b): f( 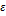) = С.

Доказательство. Построим композицию g(x) =/(х) — С., что g (х) непрерывна в [а, Ь], так как f{x) и С непрерывны. Кроме того, g(a) g(b) < 0, так как f(a) — С и аf(b)-C в силу выбора С имеют разные знаки. Поэтому (а, b): g( 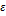) = С. Отсюда f( 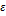) -С=0 или f( 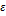) = С.

первая теорема Вейерштрасса. Пусть функция f(х) определена и непрерывна в [a, b]. Тогда f(х) является ограниченной.

Доказательство. Предположим противное: функция не огра­ничена сверху или снизу. Примем для определенности, что f(х) не огра­ничена сверху, т. е. для 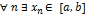> п. Последовательность {х_л} c [a, b] является ограниченной. Выделим из {х_л} сходящуюся под­последовательность {х_n}: , где с [а, b]. В точке с функция f(х) непрерывна, т. е.

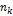Однако это невозможно, тк f > uf -f (с) при воз­растании является бесконечно большой, а не бесконечно малой ве­личиной. По аналогии обосновываем ограниченность снизу.

вторая теорема Вейерштрасса. Пусть функция f(х) определена и непрерывна в [а, b]. Тогдаf(х) имеет минимум и макси­мум в этом промежутке. Доказательство. Примем противное: f(x), оставаясь ограниченной, не достигает нижней или верхней грани. Для определенности предположим, что f(x)≠ sup {f}. Составим функцию g(x) =1/ М – f(x), где M=sup_[a,b]{f}. По условию М — f(x) > 0 для s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="18"/><w:sz-cs w:val="18"/></w:rPr><m:t>a,b</m:t></m:r></m:e></m:d><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="18"/><w:sz-cs w:val="18"/></w:rPr><m:t>. </m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> Функция g (х) непрерывна (по теореме о композиции непрерывных функций) в [a,b]. Поэтому

Обе части неравенства положительны, и его можно обратить:

Последнее неравенство невозможно, так как М - не является верхней гранью. Доказательство для случая нижней грани аналогично.

Билет №15