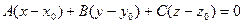Пусть x, y, x – произвольные переменные величины. Это означает, что под символами x, y, z подразумеваются какие угодно (вещественные) числа. Соотношение вида
F(x, y, z) = 0, где F(x, y, z) означает какое – нибудь выражение, содержащее x, y, z, будем называть уравнением с тремя переменными x, y, z, если F(x, y, z) = 0 есть равенство, верное не всегда, т.е. не для всяких троек чисел x, y, z.
Пусть в пространстве дана какая – нибудь поверхность и вместе с тем выбрана некоторая система координат.
Уравнение данной поверхности (в выбранной системе координат) называется такое уравнение с тремя переменными, которому удовлетворяют координаты каждой точки, лежащей на этой поверхности, и не удовлетворяют координаты никакой точки, не лежащей на ней.
Поверхность, определенная данным уравнением (в некоторой системе координат), есть место точек, координаты которых удовлетворяют этому уравнению.
Замечание. Если М (x, y, z) – переменная точка поверхности, то x, y, z называют текущими координатами.
В пространственной аналитической геометрии каждая линия рассматривается как пересечение двух поверхностей и соответственно этому определяется заданием двух уравнений. F(x, y, z)
Именно, если F(x, y, z) = 0 и f (x, y, z) = 0 суть уравнения двух поверхностей, т.е. точек, координаты которых удовлетворяют одновременно и уравнению
F(x, y, z) = 0 и f (x, y, z) = 0.
Т. о., 2 уравнения  совместно определяют линию L.
совместно определяют линию L.
Геометрическая задача разыскания точек пересечения трех поверхностей равносильна алгебраической задаче совместного решения системы трех уравнений с тремя неизвестными.
3. Уравнение плоскости:
- общее уравнение плоскости, частные случаи;
Теорема. В декартовых координатах каждая плоскость определяется уравнением первой степени.
Доказательство.
Считая заданной некоторую декартову прямоугольную систему координат, рассмотрим произвольную плоскость α и докажем, что эта плоскость определяется уравнением первой степени. Возьмем любую М0 (x0, y0, z0) лежащую на плоскости α, выберем любойвектор неравный 0 и перпендикулярный к плоскости α. Выбранный вектор обозначим буквой n., его проекции на оси координат буквами А, В, С.
Пусть M(x, y, z) - любая точка. Она лежит на плоскости α, в том и только в том случае, когда  перпендикулярна
перпендикулярна  .
.
Получим уравнение плоскости α, если выразим это условие через координаты x, y, z.
 ,
, 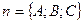 .
.
Признаком перпендикулярности двух векторов является равенство их скалярного произведения, т.е. суммы попарных произведений соответствующих координат этих векторов. Т.о.,  перпендикулярна
перпендикулярна  в том и только в том случае, когда
в том и только в том случае, когда
|
(1) – это и есть искомое уравнение плоскости α,
так как ему удовлетворяют x, y, z т. М в том и только в том случае, когда М лежит на плоскости α.
|
 . Обозначая число
. Обозначая число  , получим
, получим
Плоскость α действительно определяется уравнением первой степени.
Рассмотрим некоторые частные случаи уравнения первой степени, именно случаи, когда какие – либо из коэффициентов A, B, C, D обращаются в 0.
1) D = 0;  - определяет плоскость, проходящую через начало координат. Действительно числа x = 0, y = 0, z = 0 удовлетворяют уравнению
- определяет плоскость, проходящую через начало координат. Действительно числа x = 0, y = 0, z = 0 удовлетворяют уравнению  =>
=>
=> (0; 0; 0) Î плоскости.
2) С = 0;  - определяет плоскость параллельную оси Oz (или проходящую через эту ось). Действительно, в этом случае нормальный вектор
- определяет плоскость параллельную оси Oz (или проходящую через эту ось). Действительно, в этом случае нормальный вектор 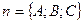 имеет нулевую проекцию на ось Oz (С = 0); следовательно, этот вектор перпендикулярен Oz, а сама плоскость параллельна ей (или проходит через нее).
имеет нулевую проекцию на ось Oz (С = 0); следовательно, этот вектор перпендикулярен Oz, а сама плоскость параллельна ей (или проходит через нее).
3) B = 0 и С = 0; уравнение Ax + D = 0 и определяет плоскость, параллельные координаты плоскости Oxz (или совпадающую с ней). Действительно, в этом случае нормальный вектор 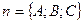 имеет нулевые проекции на оси Oy и Oz следовательно
имеет нулевые проекции на оси Oy и Oz следовательно  и
и  , а сама плоскость параллельна им (или проходит через каждую из них). Но это и означает, что плоскость, определяемая уравнением Ax + D = 0, параллельна плоскости Oyz или совпадает с ней.
, а сама плоскость параллельна им (или проходит через каждую из них). Но это и означает, что плоскость, определяемая уравнением Ax + D = 0, параллельна плоскости Oyz или совпадает с ней.
- нормальное уравнение плоскости;

Пусть дана какая – нибудь плоскость π. Проведем через (0; 0) прямую n перпендикулярную плоскости π – будем называть эту прямую нормалью, и пометим P точку, в которой она пересекает плоскость π. На нормали введем +-ое направление от точки 0 к точке P (если точка P совпадет с 0, т.е. если данная плоскость проходит через (0; 0), то + направление нормали выберем произвольно) a, b,  - углы, которые составляет направленная нормаль с осями координат, через Р – длину отрезка ОР. Выведем уравнение плоскости π, считая известными числа cos a, cosb, cos
- углы, которые составляет направленная нормаль с осями координат, через Р – длину отрезка ОР. Выведем уравнение плоскости π, считая известными числа cos a, cosb, cos  и Р. С этой целью возьмем на плоскости π любую точу М(x, y, z). Проекция
и Р. С этой целью возьмем на плоскости π любую точу М(x, y, z). Проекция  на нормаль равна ОР, а так как + направление нормали совпадает с направлением отрезка
на нормаль равна ОР, а так как + направление нормали совпадает с направлением отрезка  , то влияние этого отрезка выражается + числом.
, то влияние этого отрезка выражается + числом.
Р, т.о. прn 
 = Р (1)
= Р (1)
 => (следствие: если некоторая ось n составляет с координатными осями углы a, b,
=> (следствие: если некоторая ось n составляет с координатными осями углы a, b,  , то проекция произвольного вектора
, то проекция произвольного вектора 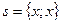 на эту ось определяется равенством: прn
на эту ось определяется равенством: прn  ).
).
прn 
 (2)
(2)
Из равенства (1) и (2) следует, что  = Р или
= Р или
 (3)
(3)
Уравнение плоскости (3) называется нормальным уравнением плоскости; в этом уравнении cos a, cosb, cos  направляющие cos нормали, Р – расстояние плоскости от начала координат.
направляющие cos нормали, Р – расстояние плоскости от начала координат.
- уравнение плоскости, проходящей через три точки;
В пространстве R3 введена прямоугольная система координат (x1; x2; x3).
Даны три точки не лежащие на одной прямой

Требуется написать уравнение плоскости, проходящей через эти три точки. Из геометрии известно, что такая плоскость существует и единственная. Так как она проходит через точку х, то ее уравнение имеет вид:
(1)  , где
, где  одновременно неравны 0. Так как она проходит еще через точки
одновременно неравны 0. Так как она проходит еще через точки  и
и  , то должны выполнятся условия:
, то должны выполнятся условия:
 (2).
(2).
Составим однородную линейную систему уравнений относительно неизвестных
(z1, z2, z3): 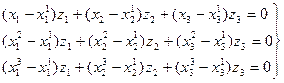 (3).
(3).
|
 есть любая точка, удовлетворяющая уравнению плоскости (1). В силу (1) и (2) системе (3) удовлетворяет нетривиальный вектор
есть любая точка, удовлетворяющая уравнению плоскости (1). В силу (1) и (2) системе (3) удовлетворяет нетривиальный вектор  поэтому определитель этой системы равен 0.
поэтому определитель этой системы равен 0.
(4).
Уравнение (4) можно еще написать и в следующем виде:
|
(5).