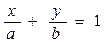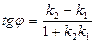Определение уравнения линии, примеры линии на плоскости

Рассмотрим соотношение вида F(x, y)=0, связывающее переменные величины x и у. Равенство (1) будем называть уравнением с двумя переменными х, у, если это равенство справедливо не для всех пар чисел х и у. Примеры уравнений: 2х + 3у = 0, х² + у² – 25 = 0,

sin x + sin y – 1 = 0.

Если (1) справедливо для всех пар чисел х и у, то оно называется тождеством. Примеры тождеств: (х + у)² - х² - 2ху - у² = 0, (х + у)(х - у) - х² + у² = 0.

Уравнение (1) будем называть уравнением множества точек (х; у), если этому уравнению удовлетворяют координаты х и у любой точки множества и не удовлетворяют координаты никакой точки, не принадлежащие этому множеству.

Важным понятием аналитической геометрии является понятие уравнения линии. Пусть на плоскости заданы прямоугольная система координат и некоторая линия α.

Определение. Уравнение (1) называется уравнением линии α (в созданной системе координат), если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии α, и не удовлетворяют координаты никакой точки, не лежащей на этой линии.

Если (1) является уравнением линии α, то будем говорить, что уравнение (1) определяет (задает) линию α.

Линия α может определятся не только уравнением вида (1), но и уравнением вида

F (P, φ) = 0, содержащим полярные координаты.

 

6. Прямая линия на плоскости:

• уравнение прямой с угловым коэффициентом;

Пусть дана некоторая прямая, не перпендикулярная, оси ОХ. Назовем углом наклона данной прямой к оси ОХ угол α, на который нужно повернуть ось ОХ, чтобы положительное направление совпало с одним из направлений прямой. Тангенс угла наклона прямой к оси ОХ называют угловым коэффициентом этой прямой и обозначают буквой К.

	К=tg α
		(1)

 

 

Выведем уравнение данной прямой, если известны ее К и величина в отрезке ОВ, которой она отсекает на оси ОУ.

(2)

y=kx+b

Обозначим через М " точку плоскости (х; у). Если провести прямые BN и NM, параллельные осям, то образуются r BNM – прямоугольный. Т. MC C BM <=>, когда величины NM и BN удовлетворяют условию: . Но NM=CM-CN=CM-OB=y-b, BN=x => учитывая (1), получаем, что точка М (х; у) С на данной прямой <=>, когда ее координаты удовлетворяют уравнению: =>

 

Уравнение (2) называют уравнением прямой с угловым коэффициентом. Если K=0, то прямая параллельна оси ОХ и ее уравнение имеет вид y = b.

• уравнение прямой, проходящей через две точки;

(4)

Пусть даны две точки М₁ (х₁; у₁) и М₂ (х₂; у₂). Приняв в (3) точку М (х; у) за М₂ (х₂; у₂), получим у₂-у₁=k(х₂ - х₁). Определяя k из последнего равенства и подставляя его в уравнение (3), получаем искомое уравнение прямой: . Это уравнение, если у₁≠ у₂, можно записать в виде:

 

Если у₁ = у_{2 ,} то уравнение искомой прямой имеет вид у = у₁. В этом случае прямая параллельна оси ОХ. Если х₁ = х₂, то прямая, проходящая через точки М₁ и М₂, параллельна оси ОУ, ее уравнение имеет вид х = х₁.

• уравнение прямой, проходящей через заданную точку с данным угловым коэффициентом;

(3)

y – y1 = k(x – x1)

Запишем уравнение прямой в виде (2), где b – пока неизвестное число. Так как прямая проходит через точку М₁ (х₁; у₁), то координаты этой точки удовлетворяют уравнению (2): у₁ = kx₁ + b. Определяя b из этого равенства и подставляя в уравнение (2), получаем искомое уравнение прямой:

 

 

Замечание. Если прямая проходит через точку М₁ (х₁;у₁) перпендикулярна оси ОХ, т.е. ее угловой коэффициент обращается в бесконечность, то уравнение прямой имеет вид

х – х₁ = 0. Формально это уравнение можно получит из уравнения (3), если разделить (3) на k и затем устремить k к ∞.

• общее уравнение прямой, частные случаи;

(5)

Аx + Вy + С = 0

Теорема. В прямоугольной системе координат Оху любая прямая задается уравнением первой степени:

 

 

и, обратно, уравнение (5) при произвольных коэффициентах А, В, С (А и В ≠ 0 одновременно) определяет некоторую прямую в прямоугольной системе координат Оху.

Доказательство.

Сначала докажем первое утверждение. Если прямая не перпендикулярна Ох, то она определяется уравнением первой степени: у = kx + b, т.е. уравнением вида (5), где

A = k, B = -1 и C = b. Если прямая перпендикулярна Ох, то все ее точки имеют одинаковые абсциссы, равные величине α отрезка, отсекаемого прямой на оси Ох.

 

Уравнение этой прямой имеет вид х = α, т.е. также является уравнение первой степени вида (5), где А = 1, В = 0, С = - α. Тем самым доказано первое утверждение.

Докажем обратное утверждение. Пусть дано уравнение (5), причем хотя бы один из коэффициентов А и В ≠ 0.

Если В ≠ 0, то (5) можно записать в виде 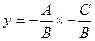. Пологая , получаем уравнение у = kx + b, т.е. уравнение вида (2) которое определяет прямую.

Если В = 0, то А ≠ 0 и (5) принимает вид . Обозначая через α, получаем

х = α, т.е. уравнение прямой перпендикулярное Ох.

Линии, определяемые в прямоугольной системе координат уравнением первой степени, называются линиями первого порядка.

Уравнение вида Ах + Ву + С = 0 является неполным, т.е. какой – то из коэффициентов равен нулю.

1) С = 0; Ах + Ву = 0 и определяет прямую, проходящую через начало координат.

2) В = 0 (А ≠ 0); уравнение Ах + С = 0 и определяет прямую параллельную Оу.

3) А = 0 (В ≠ 0); Ву + С = 0 и определяет прямую параллельную Ох.

Пусть теперь дано уравнение Ах + Ву + С = 0 при условии, что ни один из коэффициентов А, В, С ≠ 0. Преобразуем его к виду:

(6)

 

 

Уравнение (6) называется уравнением прямой «в отрезках». Числа а и b являются величинами отрезков, которые прямая отсекает на осях координат. Эта форма уравнения удобна для геометрического построения прямой.

• нормальное уравнение прямой;

Аx + Вy + С = 0 – общее уравнение некоторой прямой, а (5) x cos α + y sin α – p = 0 (7)

ее нормальное уравнение.

Так как уравнение (5) и (7) определяют одну и ту же прямую, то (А_1х + В_1у + С₁ = 0 и

А_2х + В_2у + С₂ = 0 => ) коэффициенты этих уравнений пропорциональны. Это означает, что помножив все члены уравнения (5) на некоторый множитель М, мы получим уравнение МА_х + МВ_у + МС = 0, совпадающее с уравнением (7) т.е.

МА = cos α, MB = sin α, MC = - P (8)

Чтобы найти множитель М, возведем первые два из этих равенств в квадрат и сложим:

М² (А² + В²) = cos ² α + sin² α = 1

(9)

Число М, по умножении на которое общее уравнение прямой приобретает нормальный вид, называется нормирующим множителем этого уравнения.

Замечание. Если С = 0, то знак нормирующего множителя можно выбрать по желанию.

 

Угол между двумя прямыми.

 

Рассмотрим две прямые L ₁ и L₂. Пусть уравнение L₁ имеет вид y = k₁x + b₁, где

k₁ = tg α₁, а уравнение L₂ – вид y = k₂x + b₂, где k₂ = tg α₂. Пусть φ – угол между прямыми L₁ и L₂: 0 ≤ φ < π. Из геометрических соображений устанавливаем зависимость между углами α₁, α_2, φ: α₂ = α₁ + φ или φ = α₂ - α₁ =>

, или

 

 

(1)

 

Формула (1) определяет один из углов между прямыми. Второй угол равен π – φ.