Положение всякой прямой однозначно определяется любой точкой 
, лежащей на этой прямой и углом 
, который образует эта прямая с положительным направлением оси 
. Тангенс угла (часто говорят: «угол наклона прямой к оси ») называют угловым коэффициентом прямой. Обозначим: 
.
 |
Заметим, что для прямой, параллельной оси
, угловой коэффициент 
равен нулю, а для прямой, перпендикулярной оси , угловой коэффици
Рис. 7
ент не существует. Нетрудно показать, что если прямая не перпендикулярна оси и имеет направляющий вектор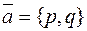 
, то угловой коэффициент 
.
Для того чтобы вывести уравнение прямой, проходящей через заданную точку 
и имеющей заданный угловой коэффициент , умножим обе части канонического уравнения (2.4) на 
и учтём, что 
. Мы получим искомое уравнение в виде 
. Если теперь ввести обозначение 
, то это уравнение примет вид
. (2.7)
Оно называется уравнением прямой с угловым коэффициентом.
Пример 23. Написать уравнение прямой, проходящей через точку 
и составляющей с осью 
угол 
.
Решение. Найдем угловой коэффициент прямой 
Далее подставляя в уравнение 
получим 
или 
Взаимное расположение двух прямых на плоскости
Условие совпадения прямых. Две прямые 
и 
совпадают тогда и только тогда, когда 
и 
.
Условие параллельности прямых.
1) Две прямые и параллельны тогда и только тогда, когда и 
.
2) Две прямые 
и 
параллельны или совпадают тогда и только тогда, когда их нормальные векторы 
и 
коллинеарны.
Условие перпендикулярности прямых.
1) Две прямые и перпендикулярны тогда и только тогда, когда 
.
2) Две прямые и перпендикулярны тогда и только тогда, когда их нормальные векторы и перпендикулярны.
Пример 24. Параллельны ли прямые 
и 
?
Решение. Приведем уравнения прямых к виду прямой с угловым коэффициентом. Получаем 
Уравнение первой прямой 
, второй -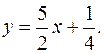 
Так как 
прямые параллельны.
Угол между прямыми
Даны прямые 
и 
. Требуется найти угол между ними.
 |
Рис. 8
Вычислим
. (2.8)
Обозначения см. на рис. 8.
Для прямых, заданных уравнениями и формула (2.8) примет вид
Пример 25.
Найти тангенс угла между прямыми 
и 
.
Решение. Найдем угловые коэффициенты заданных прямых: 
Воспользуемся формулой (2.8) и найдем 
Расстояние от точки до прямой
На плоскости даны 
и прямая 
. Тогда расстояние от точки 
до прямой 
находится по формуле
(2.9)
Пример 26. Вычислить расстояние от точки 
до прямой 
Решение. Для заданной прямой вектором нормали является вектор 
Подставим в формулу (2.9) 
и вычислим расстояние от точки до прямой
ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
Общее уравнение плоскости
Уравнение
(3.1)
в котором 
, называется общим уравнением плоскости.
3.2 Уравнение плоскости, проходящей через данную точку 
перпендикулярно 
.
Пусть в пространстве 
плоскость 
задана точкой и вектором 
, перпендикулярным этой плоскости. Выведем уравнение плоскости . Возьмем на ней произвольную точку 
и составим вектор 
Рис. 9
Вектор 
, поэтому 
, т.е.
(3.2)
Вектор называется нормальным вектором плоскости, а уравнение (3.2) называется уравнением плоскости по точке и нормальному вектору.
Пример 27. Написать уравнение плоскости, проходящей через точку 
перпендикулярно вектору нормали 
Решение. Воспользуемся уравнением (3.1). В нашей задаче 
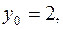
Имеем 
. Раскрывая скобки и приводя подобные члены получаем общее уравнение прямой 
