Аналитическая геометрия
Пример 1.
В треугольнике с вершинами 
, 
, 
проведена высота 
. Написать уравнение этой высоты.
Решение.
Напишем уравнение стороны 
,
или 
. Откуда определяем нормальный вектор 
прямой 
, который является направляющим вектором для высоты 
.
Составим уравнение прямой, проходящей через точку 
параллельно направляющему вектору 
:
, или 
.
Ответ: 
.
Пример 2.
Составить уравнение прямой, проходящей через точку пересечения прямых 
и 
параллельно прямой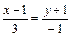 
.
Решение.
Найдем точку пересечения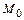 
прямых и , решая систему двух линейных уравнений с двумя неизвестными:
.
Искомая прямая параллельна прямой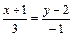 
. Следовательно, направляющим вектором искомой прямой может быть выбран вектор 
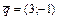. Таким образом, прямая, проходящая через точку 
параллельно направляющему вектору 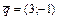, может быть записана в виде 
.
Ответ: 
.
Пример 3.
Написать уравнение прямой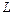 
, параллельной двум заданным прямым: 
, 
, и проходящей посередине между ними.
Решение.
Так как вектор 
, нормальный к заданным прямым 
и 
, является в то же время нормальным вектором и к прямой 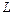, то достаточно найти какую-нибудь точку 
, лежащую посередине между и . Из уравнений:
,
.
Тогда точка 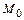, делящая отрезок 
пополам, лежит посередине между и . Находим координаты точки :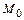
.
Поэтому уравнение прямой 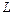, проходящей через точку 
перпендикулярно нормальному вектору имеет вид: 
.
Ответ: 
.
Пример 4. Составить уравнение плоскости, проходящей через точку 
параллельно плоскости 
.
Решение. Искомую плоскость обозначим через 
. Тогда их нормальные векторы параллельны. Поэтому нормальный вектор 
плоскости 
можно принять за нормальный вектор искомой плоскости 
. Тогда уравнение плоскости, проходящей через точку 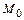перпендикулярно нормальному вектору 
примет вид:
или 
.
Ответ: 
.
Пример 5. Написать уравнение плоскости , проходящей через точки 
и 
параллельно вектору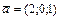 
.
Решение. Так как вектор 
не коллинеарен вектору 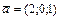, то задача имеет единственное решение. Выберем произвольную точку 
и найдем вектор 
. Таким образом, 
, или
.
Ответ: 
Пример 5. Составить каноническое уравнение прямой, проходящей через точку 
параллельно прямой 
.
Решение. За направляющий вектор искомой прямой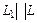 
можно принять направляющий вектор 
. Тогда, используя уравнение прямой, проходящей через точку 
параллельно направляющему вектору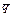 
, получим
.
Ответ: .
Пример 6. Заданы скрещивающиеся прямые 
и 
. Найти расстояние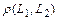 
между этими прямыми.
Решение.
Найдем уравнение плоскости проходящей через прямую параллельно прямой .
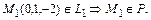
В качестве нормального вектора к этой плоскости Р, возьмем вектор 
где 
- направляющие векторы прямых и . Следовательно,
.
Уравнение плоскости Р:
Расстояние 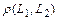равно расстоянию от любой точки прямой , например, точки 
, до плоскости Р. Нормальное уравнение плоскости имеет вид:
.
Откуда
Ответ: 
Пример 7. Найти точку, симметричную с началом координат относительно плоскости
Решение.
1. Напишем уравнение прямой 
перпендикулярной плоскости Р, используя каноническое уравнение прямой:
где 
- направляющий вектор прямой. В качестве 
- нормальный вектор плоскости Р. Следовательно:
2. Найдем точку пересечения 
с плоскостью Р:
3. Отрезок 
делится в точке 
пополам. Следовательно, если
то
Ответ: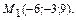 
Пример 8. Написать уравнение параболы с вершиной в начале координат, если известно, что фокус параболы находится в точке 
Решение.
Если 
, то фокус параболы находится на оси 
, причем левее начала координат. Уравнение параболы имеет вид
.
Таким образом, 
.
Ответ: .
Пример 9. Составить каноническое уравнение эллипса, зная, что он проходит через точки 
и 
.
Решение. Возьмем каноническое уравнение эллипса 
и вместо текущих координат подставим координаты точек и 
. Получим систему уравнений:
.
Определим параметры эллипса 
и 
, решая систему уравнений. Обозначив 
, 
сведем данную систему к следующей системе:
.
Следовательно, искомое уравнение эллипса будет 
.
Ответ: .
Пример 10. Написать уравнение гиперболы с асимптотами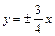 
, проходящими через точку 
. Найти расстояние между ее вершинами.
Решение. Так как точка лежит на гиперболе, то ее координаты должны удовлетворять каноническому уравнению:
, т.е. уравнению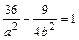 
.
Кроме того, из уравнений асимптот гиперболы имеем 
.
Решая полученную систему двух уравнений:
,
т.е. уравнение гиперболы имеет вид 
.
Расстояние между вершинами определяем из условия: 
.
Ответ: ; 
.
Пример 11. Дана гипербола 
. Найти эллипс, фокусы которого совпадают с фокусами данной гиперболы, проходящей через точку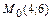 
.
Решение. Обозначим параметры данной гиперболы через 
, 
, 
и найдем их, приведя уравнение гиперболы к каноническому виду: 
.
Так как по условию фокусы искомого эллипса и данной гиперболы совпадают, то для эллипса 
.
Рассмотрим каноническое уравнение эллипса и подставим в него координаты точки :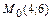
.
Ответ: 
.
Пример 12. Установить, что плоскость 
пересекает эллипсоид 
по эллипсу, найти его полуоси и вершины.
Решение. Сечение эллипсоида плоскостью определяется системой:
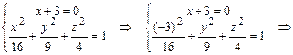
т.е. является эллипсом.
Полуоси полученного эллипса равны:
.
Вершинами эллипса являются точки
; 
; 
; 
.
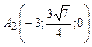Ответ: 
;
; ; ;
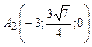