При синтезе контуров регулирования используется два типа оптимальных настроек: настройка на модульный оптимум (МО) и настройка на симметричный оптимум (СО). Выбор типа настройки определяется требованиями к статическим и динамическим характеристикам при отработке управляющих воздействий и возмущений, действующих внутри контура регулирования.
Модульный оптимум настройки контуров регулирования
Считается, что замкнутый контур регулирования с единичной обратной связью настроен на модульный оптимум, если он имеет передаточную функцию второго порядка вида
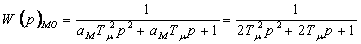, (6.1)
где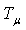 
- малая постоянная времени некомпенсируемого апериодического звена;
аМ =1ч4 – коэффициент модульной настройки;
аМ =2 - стандартный коэффициент настройки контура.
Эту передаточную функцию можно записать в форме, соответствующей колебательному звену
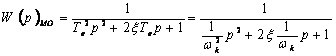, (6.2)
где 
- эквивалентная постоянная времени колебательного звена;
- частота недемпфируемых колебаний;
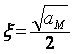- коэффициент демпфирования колебаний.
Для стандартной настройки 
, 
.
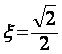Действительная частота колебаний звена второго порядка определяется соотношением
. (6.3)
Следовательно, с возрастанием коэффициента демпфирования действительная частота колебаний в контуре регулирования уменьшается. При стандартной настройке на МО, когда аМ= 2,
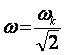. (6.4)
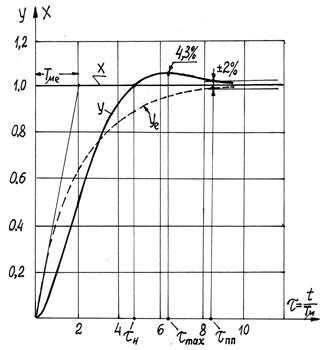
Переходный процесс отработки ступенчатого задающего воздействия представлен на рис.6.2. Он описывается уравнением
|
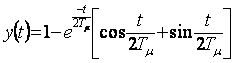. (6.5)
И имеет следующие показатели качества: время переходного процесса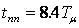 
; время нарастания 
; время первого максимума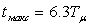 
; перерегулирование 
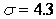%; число колебаний 
.
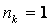Следовательно, в контуре, настроенном на МО, достигается компромисс между быстродействием и перерегулированием, когда при сравнительно хорошем быстродействии
(
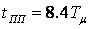) перерегулирование составляет
менее 5% (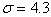
%). По динамическим
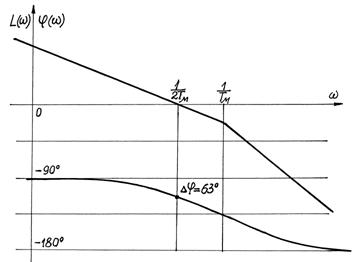
показателям этот переходный процесс можно считать приемлемым для многих технологических установок. Разомкнутый контур, настроенный на МО, имеет передаточную функцию
|
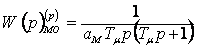. (6.6)
|
Так как эта передаточная функция содержит одно интегрирующее звено, то контур, настроенный на МО, является однократно интегрирующей системой. В соответствии с (6.6) ЛАЧХ и ЛФЧХ разомкнутого контура, настроенного на МО, приведены на рис.6.3, где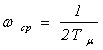 
частота среза, 
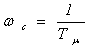- частота сопряже-
ния асимптот, а запас по фазе на частоте среза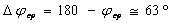 
.
Таким образом, задачей синтеза контура при настройке на МО является выбор регулятора - последовательного корректирующего звена с такой передаточной функцией, чтобы разомкнутый контур имел передаточную функцию (6.6).
Симметричный оптимум настройки контуров регулирования
Считается, что замкнутый контур регулирования с единичной отрицательной обратной связью настроен на симметричный оптимум (СО), если он имеет передаточную функцию третьего порядка вида
, (6.7)
где 
- малая постоянная времени некомпенсируемого апериодического звена;
ас = 3,5¸8 – коэффициент симметричной настройки;
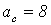- стандартный коэффициент настройки контура.
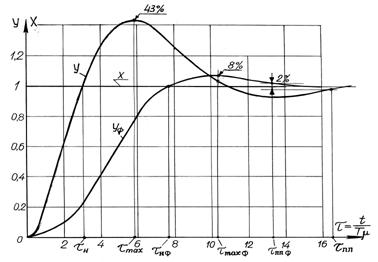
Для контура, имеющего стандартную настройку на СО (ас =8), переходный процесс отработки ступенчатого задающего воздействия представлен на рис.6.4. Он описывается уравнением
(6.8)
и имеет следующие показатели качества: время переходного процесса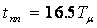 
; время нарастания 
; время первого максимума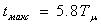 
; время первого минимума 
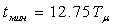; перерегулирование 
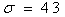%; число колебаний 
.
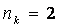Из анализа показателей качества следует, что они в значительной степени отличаются от показателей контура, настроенного на МО.
| ||
| ||
Большое перерегулирование, равное s= 43 %, обусловлено влиянием форсирующего звена W(p)= 4 Tp+ 1 в числителе передаточной функции (6.7). Перегулирование можно значительно уменьшить, если скомпенсировать числитель передаточной функции, установив на входе управления контура апериодическое звено (фильтр) с постоянной времени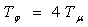 
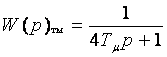. (6.9)
Тогда передаточная функция по задающему воздействию при стандартной настройке запишется в следующем виде
. (6.10)
Для контура, настроенного на СО с фильтром на входе, переходный процесс отработки ступенчатого задающего воздействия представлен на рис.6.4. Он описывается уравнением
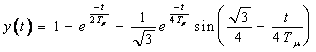(6.11)
и имеет следующие показатели качества: время переходного процесса 
; время нарастания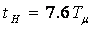 
; время первого максимума 
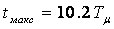; перерегулирование 
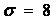%; число колебаний 
.
Следовательно, за счет компенсирующего действия фильтра на входе управления контура достигнуто значительное улучшение динамических показателей.
|
Разомкнутый контур, настроенный на СО, имеет передаточную функцию
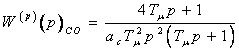. (6.12)
|
Контур, настроенный на СО, содержит в прямой цепи регулирования два интегрирующих звена и поэтому является двукратноинтегрирующей системой. В соответствии с (6.12) на рис.6.5 приведены ЛАЧХ и ЛФЧХ разомкнутого контура, настроенного на СО, где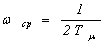 
частота среза, 
- первая частота сопряжения асимптот,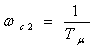 
- вторая частота
сопряжения. Запас по фазе на частоте среза
Dj= 38°. ЛАЧХ имеет симметричную форму относительно частоты среза с наклонами асимптот -40дб/дек, -20дб/дек, -40дб/дек. Поэтому такой настройке присвоено название симметричный оптимум. Настройку контура можно несколько улучшить, увеличив в 1,25 раза частоту среза контура, взяв соответственно коэффициент настройки ас= 6,4. В этом случае реализуется настройка на “минимальную колебательность”. Сопрягающие частоты wс 1, wс 2при этом должны оставаться неизменными. Применение такой настройки несколько снижает перерегулирование и увеличивает быстродействие, а именно: 
, s@ 42 %. Запас по фазе уменьшается всего на 3° и становится равным Djср= 35°.
Когда в прямой цепи контура регулирования имеется только одно апериодическое звено с малой постоянной времени, то оно и является звеном с некомпенсируемой постоянной времени.
Если в прямой цепи контура регулирования имеется несколько апериодических звеньев с малыми постоянными времени, то для расчета параметров регулятора эти инерционные звенья необходимо заменить одним эквивалентным апериодическим звеном с постоянной времени Тmе.
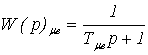, (6.13)
где 
- эквивалентная некомпенсируемая постоянная времени.
