Синтез замкнутых систем регулирования

Обычно под синтезом замкнутой системы регулирования подразумевается расчет и включение в контур регулирования дополнительных динамических звеньев, корректирующих устройств, с целью достижения требуемых показателей качества в установившемся и переходном режимах, которые задаются в технических требованиях.

На практике наибольшее распространение получил частотный метод синтеза корректирующих устройств с использованием логарифмических амплитудных (ЛАЧХ) и логарифмических фазовых (ЛФЧХ) частотных характеристик разомкнутой системы регулирования.

 

Содержание технических требований

В качестве исходных данных для синтеза принимаются технические требования к точности системы регулирования в установившихся режимах работы и динамические показатели переходного процесса отработки ступенчатого задающего воздействия.

Технические требования к системе регулирования обычно составляются на основании параметров технологического процесса, в реализации которого используются система регулирования.

Точность системы регулирования в установившемся режиме при отработке воздействия f_з называют статизмом по воздействию f_з.

Статизм определяется соотношением

(5.1)

,

где Y_з – заданное значение выходной координаты;

Y_х – выходная координата после отработки воздействия f_з.

Если статизм равен нулю, т.е. S _{f з} =0, то система называется астатической по входу f_з.

На рисунке 5.1. приведен график переходного процесса отработки системой регулирования ступенчатого воздействия f_з.

К динамическим показателям переходного процесса отработки ступенчатого воздействия относятся:

1. Время переходного процесса t_пп, с,

2. Перерегулирование s %,

3. Число колебаний регулируемой координаты n_к,

4. Время нарастания до заданного значения t_нр, с.

Время переходного процесса t_пп – момент вхождения выходной координаты Х в зону допустимых отклонений, после которого она уже не выходит из этой зоны.

Перерегулирование выходной координаты s % вычисляется из соотношения

(5.2)

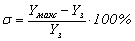
Рис.5.1 График переходного процесса отработки системой регулирования

ступенчатого воздействия f_з

Ч исло колебаний n_к равно числу переходов выходной координаты через уровень заданного значения до попадания в зону допустимых отклонений.

Время нарастания t_нр – момент первого достижения регулируемой координатой уровня заданного значения.

 

Общий порядок синтеза корректирующего устройства

И вид желаемой ЛАЧХ

На основании технических требований по точности, времени переходного процесса t_пп и допустимому перерегулированию s выбирается вид желаемой ЛАЧХ и ЛФЧХ разомкнутой скорректированной системы. В теории регулирования было выявлено, что существует определенная взаимосвязь между ЛАЧХ и ЛФЧХ разомкнутой системы и точностью, временем переходного процесса t_пп и перерегулированием s в замкнутом контуре регулирования.

Типовые желаемые ЛАЧХ и ЛФЧХ разомкнутых скорректированных систем приведены на рисунке 5.2 а, б, в. Они имеют асимптоты с наклоном –0, -20, -40 ДБ/дек (рис. 5.2.а); -20, -20, -40 ДБ/дек (рис.5.2.б); -40, -20, -40ДБ/дек (рис.5.2.в). При этом первым указывается наклон низкочастотной асимптоты.

Разомкнутый контур с ЛАЧХ вида 0; -20; -40 Дб/дек имеет передаточную функцию

(5.3)

и содержит три звена: одно усилительное и два апериодических.

На рис. 5.2.а ЛФЧХ определяется соотношением

j(w)= - arctg T₁w - arctg T₂w

Разомкнутый контур с ЛАЧХ вида –20; -20; -40 Дб/дек имеет передаточную функцию

(5.4)

,

и содержит три звена: одно усилительное с К=1/Т_и, одно интегрирующее и одно апериодическое звенья.

На рис. 5.2.б ЛФЧХ определяется соотношением

j(w)= -90 - arctg T₂w

Разомкнутый контур с ЛАЧХ вида –40; -20; -40 Дб/дек содержит два интегрирующих звена и имеет передаточную функцию

(5.5)

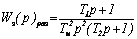
и содержит пять звеньев: одно усилительное с К=1/Т²_и, два интегрирующих, одно форсирующее и одно апериодическое звенья.

 

На рисунке 5.2.в ЛФЧХ определяется соотношением

j(w)= -2×90 + arctg T₁w - arctg T₂w

На каждой ЛАЧХ рис. 5.2 можно выделить три участка:

- низкочастотный;

- среднечастотный;

- высокочастотный.

Динамические показатели замкнутой системы регулирования определяются среднечастотным участком ЛАЧХ, который располагается слева и справа относительно частоты среза w_ср, где ЛАЧХ пересекает ось частот.

Чтобы система была устойчивой и имела качественный переходный процесс в отношении перерегулирования s и числа колебаний n_к, среднечастотный участок ЛАЧХ должен иметь наклон –20 Дб/дек, а его протяженность составлять не менее одной декады. Время переходного процесса t_пп и частота среза w_ср связаны следующим соотношением:

(5.6)

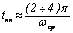
Перерегулирование в переходном процессе замкнутой системы регулирования и число колебаний зависит от запаса по фазе на частоте среза

(5.7)

Dj_ср=180°- j_{ср ,}

где j_ср – сдвиг по фазе сигнала в разомкнутом контуре регулирования на частоте среза.

 

 

Рис. 5.2 ЛАЧХ и ЛФЧХ разомкнутых скорректированных систем регулирования

с ВЧ – участком (-40 ДБ/дек)

рис. 5.2.а - –0, -20, -40 ДБ/дек; рис.5.2.б - -20, -20, -40 ДБ/дек;

рис. 5.2.в --40, -20, -40 ДБ/дек

 

 

Чем больше запас по фазе, тем меньше перерегулирование s. Существует следующая зависимость:

1. при запасе по фазе Dj_ср=(25-35)° перерегулирование составляет s=(80-50)%;

2. при запасе по фазе Dj_ср=(40-50)° перерегулирование составляет s=(45-25)%;

3. при запасе по фазе Dj_ср=(55-65)° перерегулирование составляет s=(20-5)%;

4. при запасе по фазе Dj_ср больше 70° перерегулирование отсутствует.

Поэтому в зависимости от допустимого по техническим требованиям перерегулирования, разомкнутый контур регулирования должен иметь вполне определенный запас по фазе на частоте среза.

Низкочастотный участок ЛАЧХ определяет точность замкнутой системы регулирования и лежит слева от среднечастотного вплоть до инфранизких частот. Низкочастотный участок ЛАЧХ может иметь наклон 0Дб/дек, -20 Дб/дек или –40 Дб/дек.

Система регулирования, у которой низкочастотный участок ЛАЧХ имеет наклон 0Дб/дек, называется статической или система с нулевым порядком астатизма, так как в ней установившаяся ошибка при отработке ступенчатого задающего воздействия F_з(p)=А(р) равна конкретному конечному значению, которое определяется уравнением

(5.8)

Система регулирования, у которой низкочастотный участок ЛАЧХ имеет наклон –20 Дб/дек, называется астатической системой с астатизмом первого порядка. В ней установившаяся ошибка при отработке ступенчатого воздействия F_з(p)=А(р) равна нулю, так как числитель передаточной функции W(р)_x®d содержит оператор р в первой степени стоящий сомножителем

(5.9)

.

(5.10)

Если на входе такой системы действует линейно изменяющееся воздействие, для которого F_з(р)=В_з/р, то установившаяся ошибка отработки такого воздействия не будет равна нулю, а будет определяться соотношением

.

Система регулирования, у которой низкочастотный участок ЛАЧХ имеет наклон

-40Дб/дек, называется астатической системой с астатизмом второго порядка. В ней установившиеся ошибки при отработке ступенчатого воздействия F_з(р)=А(р) и линейно изменяющегося F_з(р)=В_з/р равны нулю, так числитель передаточной функции содержит оператор р во второй степени стоящий сомножителем

(5.11)

.

Если на входе такой системы действует параболическое входное воздействие, для которого F_з(р)=С_з/р², то установившаяся ошибка отработки такого воздействия будет определяться соотношением

(5.12)

.

Следовательно, наибольшей точностью обладает система регулирования, имеющая второй порядок астатизма с ЛАЧХ вида –40; -20; -40 Дб/дек. Однако, в таком контуре запас по фазе на частоте среза Dj_ср обычно составляет меньше 40°, как оказано на рисунке 5.2.в. Поэтому перерегулирование при отработке ступенчатого задающего воздействия составляет около 40-60 %, а число колебаний n_к=2 или больше.

Выбор наклона низкочастотного участка желаемой ЛАЧХ зависит от конкретных технических требований к системе регулирования.

Высокочастотный участок ЛАЧХ располагается правее среднечастотного участка вплоть до ультравысоких частот, когда w®:. Наклон этого участка может быть –40 Дб/дек, но чаще все-таки бывает –60 Дб/дек и более. От наклона высокочастотного участка ЛФЧХ зависит предел, к которому стремится ЛАЧХ на высоких частотах. При наклоне –40 Дб/дек - j_макс=-180°, при наклоне –60 Дб/дек - j_макс=-270°, а при наклоне –80 Дб/дек -j_макс=-360°. Если высокочастотный участок ЛАЧХ имеет наклон –60 Дб/дек или больше, то график ЛФЧХ пересекает границу -180°, как показано на рисунке 5.3. В точке пересечения с границей -180° запас по фазе Dj равен нулю. На частоте точки пересечения определяется запас по амплитуде DL_зап в замкнутом контуре регулирования. Это очень важный показатель системы регулирования. В реальных системах по разным причинам коэффициент усиления может изменяться в некоторых пределах, но при этом система регулирования не должна терять устойчивость. Предел допустимого изменения коэффициента усиления находится из соотношения

DK_доп<10^DLзап/20. (5.13.)

Считается, что целесообразный запас по амплитуде должен составлять не менее 6 Дб, т.е. DL_зап ³6 Дб _.

При таком запасе суммарный коэффициент усиления может увеличиться в 2 раза до того, как система регулирования окажется на границе устойчивости. В контурах регулирования, у которых высокочастотный участок ЛАЧХ имеет наклон –40 Дб/дек, ЛФЧХ стремится к асимптоте -180°, поэтому замкнутая система регулирования имеет бесконечно большой запас по амплитуде, так как DL_зап=: при w®:.

При фиксированной величине частоты w_ср и протяженности среднечастотной части ЛАЧХ наклон высокочастотного участка влияет на запас по фазе на частоте среза Dj_зап и, следовательно, на перерегулирование в переходном процессе при отработке ступенчатого воздействия. Уменьшение запаса по фазе при наклоне высокочастотного участка –60 Дб/дек показано на рис. 5.3.

 

 

Рис. 5.3 Типовые ЛАЧХ и ЛФЧХ скорректированных систем с ВЧ – участком

(-60 ДБ/дек) рис. 5.3.а - –20, -20, -60 ДБ/дек; рис.5.3.б - -40, -20, -60 ДБ/дек

Наклон высокочастотного участка во многом определяется передаточной функцией исходной нескорректированной системы и возможностью реализации корректирующего устройства.

Форма и параметры желаемой ЛАЧХ и ЛФЧХ определяются техническими требованиями к системе регулирования t_ппж, d x, d f, s, S₃, S_f.

1) Частота среза желаемой ЛАЧХ w_срж=(2¸4)p/t_ппж;

2) Наклон среднечастотного участка –20 Дб/дек;

3) Протяженность среднечастотного участка ³ 1 дек;

4) Наклон низкочастотного участка составляет:

а) для статических систем 0 Дб/дек;

б) для астатических систем первого порядка средней точности –20 Дб/дек;

в) для астатических систем второго порядка высокой точности –40 Дб/дек.

5) Наклон высокочастотного участка определяется наличием динамических звеньев с малыми постоянными времени в исходной неизменяемой части системы

редко –40 Дб/дек.

обычно -60 Дб/дек;

или –80 Дб/дек;

Исходя из сформулированных правил выбора желаемой ЛАЧХ и ЛФЧХ, можно записать три передаточные функции разомкнутого контура, соответствующие трем вариантам желаемых ЛАЧХ:

1 – (0; -20; -60) Дб/дек;

2 – (-20; -20; -60) Дб/дек;

3 – (-40; -20; -60) Дб/дек.

, (5.14)

где - частота среза желаемой ЛАЧХ

, (5.15)

где – частота среза желаемой ЛАЧХ.

(5.16)

,

где – частота среза желаемой ЛАЧХ;

- малая постоянная времени.

- постоянная времени форсирующего звена.

Зная передаточную функцию исходной нескорректированной системы и желаемую передаточную функцию системы, обладающей требуемыми показателями, можно вычислить передаточную функцию корректирующего устройства W(р)_ку, используя следующее соотношение W(р)_ж=W(р)_куW(р)_исх ,

(5.17)

тогда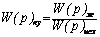

Техническая реализация корректирующего устройства с конкретной передаточной функцией выполняется путем последовательного включения типовых динамических звеньев, построенных на пассивных R, С элементах или на операционных усилителях постоянного тока (ОУ), охваченных R-С обратными связями и имеющих R-С- элементы во входных цепях. Передаточная функция такого усилителя определяется соотношением

(5.18)

,

где Z_ос(р) и Z_вх(р) операторные сопротивления цепи обратной связи и входной цепи с учетом того, что Z(р)_R= R, Z(р)_С= 1/Ср, Z(р)_L= Lр.

Примеры типовых схем корректирующих звеньев, реализованных на ОУ, приведены на рис. 5.4 – 5.10.

На рис. 5.4 приведена схема усилительного звена с передаточной функцией

(5.19)

На рис. 5.5 приведена схема интегрирующего звена с передаточной функцией

(5.20)

,

где Т_и=С_осR_вх – постоянная времени интегрирования.

На рис. 5.6 приведена схема дифференциально-инерционного звена с передаточной функцией

,

где Т_д=С_вхR_ос – постоянная времени дифференцирования,

Т_а= С_вхR_вх – постоянная времени инерционного звена.

Обычно выбирают Т_д>>Т_а, т.е. R_вх<<R_ос. В этом случае по своим динамическим свойствам звено приближается к идеальному дифференцирующему. Желательно, чтобы Т_а£ 0,01Т_д, что достигается, когда резисторы R_вх и R_ос отличаются в 100 раз.

На рис. 5.7 приведена схема инерционного звена с передаточной функцией

(5.21)

,

где К=R_ос/R_вх – коэффициент усиления,

Т=С_осR_ос – постоянная времени.

На рис. 5.8. приведена схема форсирующего звена с передаточной функцией

 

 

Рис. 5.4 Усилительное звено

Рис. 5.5 Интегрирующее звено

 

 

Рис. 5.6 Дифференциально-инерционное звено (реальное дифференцирующее)

Рис. 5.7 Инерционное звено

 

 

 

Рис.5.8 Интегрально-форсирующее звено (ПИ-звено)

Рис. 5.9 Форсирующее звено

 

 

 

Рис. 5.10 Интегрально-дважды форсирующее звено (ПИД -звено)

(5.22)

,

где К=R_ос/R_вх – коэффициент усиления

Т_ф=С_ос R_ос – постоянная времени форсирования.

На рис. 5.9 приведена схема интегрально-форсирующего звена с передаточной функцией

(5.23)

,

где Т_ф=С_ос R_ос – постоянная времени форсирования,

Т_и=С_ос R_вх – постоянная времени интегрирования.

Часто это звено называют пропорционально-интегральным (ПИ -регулятором), так как после почленного деления числителя на знаменатель можно записать

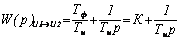, (5.24)

где 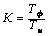- коэффициент усиления пропорционального слагаемого.

На рис. 5.10 приведена схема интегрально - дважды форсирующего звена с передаточной функцией

(5.25)

,

где Т_ф1=С_ос R_ос – первая постоянная времени форсирования,

Т_ф2=С_вх R_ос – вторая постоянная времени форсирования,

Т_и=С_ос R_вх – постоянная времени интегрирования.

Часто это звено называют пропорционально - интегрально- дифференциальным (ПИД - регулятором), так как после перемножения двухчленов в числителе и почленного деления числителя на знаменатель получается

(5.26)

,

где - коэффициент усиления,

- постоянная времени дифференцирования.