В этом случае наглядная физическая трактовка условий устойчивости практически невозможна. Поэтому целесообразно воспользоваться принципом аргумента для вспомогательной функции
j (p) = 1 + Wp(p) = 1 +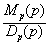 
= 
= 
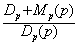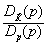, (4.17)
где Dp(p) и Dз(p) - характеристические многочлены соответственно замкнутой и разомкнутой систем. При p=jw
j(jw) =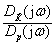 
и D arg j(jw) = D arg Dз(jw) - D arg Dp(jw). (4.18)
0 £ w £+ ¥ 0 £ w £+ ¥ 0 £ w £+ ¥
Если разомкнутая система неустойчива и характеристическое уравнение Dp(p)=0 имеет m корней с положительной действительной частью, то условие устойчивости системы в замкнутом состоянии запишется на основании (4.15) и (4.18) в следующем виде:
D arg j(jw) = n×p/2 - (n - 2m)×p/2 = 2p× m /2. (4.19)
0 £ w £+ ¥
Это значит, что в этом случае условием устойчивости замкнутой системы является охват годографом вектора j(jw) начала координат своей комплексной плоскости m /2 раз в положительном направлении при изменении w от 0 до + ¥. Однако использовать такую методику анализа устойчивости неудобно. Если же на основании (4.17) учесть, что
j (p) = 1 + Wp(p) или Wp(p) = j (p)- 1. (4.20)
Это означает, что j (p) и Wp(p) отличаются только постоянным смещением на единицу, т.е. началу координат на плоскости j (p) соответствует на плоскости Wp(p) точка с координатами (- 1, j0).
Вместо подсчета числа охватов АФХ разомкнутой системы точки с координатами (- 1, j0) целесообразно подсчитать разность между числом положительных (сверху вниз) и отрицательных переходов (снизу вверх) отрезка (-1 ¸-¥) действительной оси АФХ разомкнутой системы (в частотном диапазоне от 0 до + ¥).Для устойчивости системы в замкнутом состоянии эта разность должна быть равна m/2, где m - число корней характеристического уравнения разомкнутой системы с положительной действительной частью.
Примечание. Если АФХ разомкнутой системы начинается (при w =0) на отрезке (-1¸-¥) действительной оси, то учитывается 1/2 перехода с соответствующим знаком.
Если разомкнутая система нейтрально устойчива, т.е. в состав Wp(p) входят интегрирующие звенья, то для анализа устойчивости замкнутой системы АФХ разомкнутой системы должна быть дополнена окружностью бесконечно большого радиуса, проходящей в отрицательном направлении число квадрантов, соответствующих числу интегрирующих звеньев.
Пример 4.2. Передаточная функция разомкнутой системы
Wp(p) =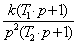 
.
Выполнить анализ устойчивости замкнутой системы с помощью критерия Найквиста для двух случаев: T1<<T2 и T1>>T2.
Характеристическое уравнение разомкнутой системы
p2(T2× p + 1) = 0
имеет корни p1,2 = 0 и p3 = - 1/T2, т.е. эта система нейтрально устойчива и m=0.
АФХ разомкнутой системы показаны на рис. 4.4.
При T1<<T2 АФХ разомкнутой системы пересекает один раз отрезок (‑1¸‑¥) вещественной оси в отрицательном направлении, т.е. условие устойчивости замкнутой системы не выполняется.
При T1>>T2 разность между числом положительных и отрицательных переходов АФХ разомкнутой системы отрезка вещественной оси (-1¸ -¥) равна 1-1=0 и m=0, т.е. условие устойчивости замкнутой системы выполнено.
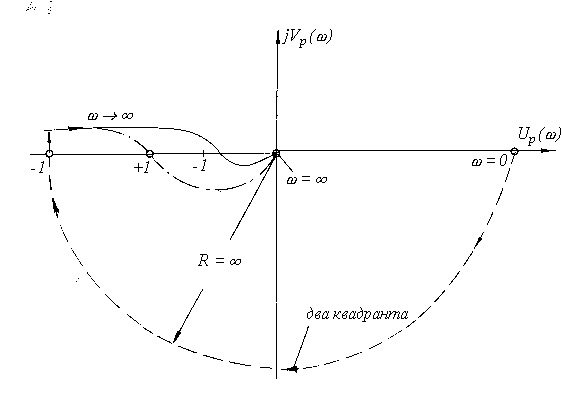
Рис. 4.4. АФХ разомкнутой системы, рассматриваемой в примере 4.2. штрихпунктирной линией обозначена основная часть АФХ Wp(jw) для случая T1>>T2
