Развертки поверхностен. Развертывание поверхности многогранников

Развертка— плоская (|mi yp^. получающаяся при совмещении поверхности с плоскостью. При совме­щении всех граней многогранника с плоскостью в такой последовательности, в которой они размещены в многограннике, получается развертка его поверхности. Для построения развертки нужно найти нату­ральную величину всех граней многогранника и фигуры сечения. Три вида разверток: точные (призмы, пирамиды); приближенные (поверхности вращения заменяют многогранной поверхностью); условные (поверхности заменяются абсолютно другой).

19. Пересечение кривых поверхностей плоскостью частною положения. Линии конических сече­ний.

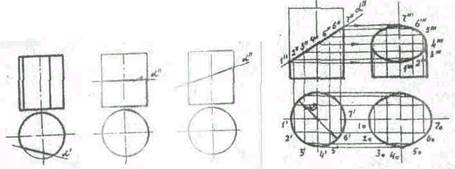
При пересечении цилиндра плоскостью, параллельной оси, получается плоская фигура в виде прямо­угольника или параллелограмма. Если секущая плоскость перпендикулярна к оси цилиндра, то в ре­зультате сечения этой плоскостью получается круг. В общем случае, если секущая плоскость наклонена к оси цилиндра, в сечении поучается эллипс.

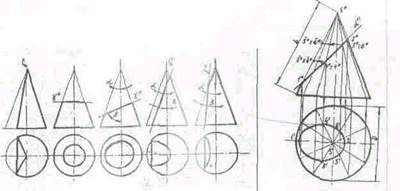
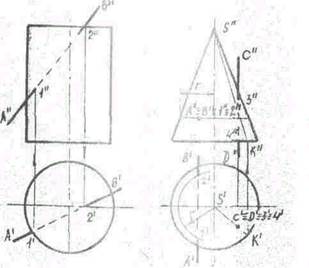
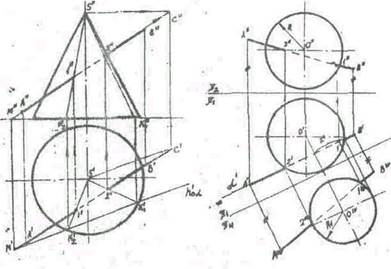
При пересечет-] и конуса секущей плоскостью, в зависимости от ее направления получаются разные фи­гуры, ограниченные линиями, которые называются линиями конических сечений. Если секущая плос­кость проходит через вершину конуса, в его сечении получается треугольник. В результате пересечения конуса плоскостью, перпендикулярной к его оси вращения, получается круг. Если плоскость наклонена к оси вращения конуса и не проходит через его вершину, в сечении, в результате от величины угла на­клона секущей плоскости к оси конуса, получатся: при Zp > Zo, — эллипс; при Zp=Za — ограничен­ная парабола; при Zp < Za - ограниченная гипербола, где a — половина угла при вершине конуса. 20. Развертывание поверхш сти прямого кругового конуса и цилиндра. Для построения развертки усеченной цилиндрической поверхности на горизонтальной прямой отклады­вают длину окружности осноиания, равную ttD, и-делят её на 12 равных частей. Из точек деления вос­станавливают псрпешЙ^пифьт к отрезку ttd, на них откладывают действительные длины образующих цилиндра от основания до секущей плоскости, которые взяты с фронтальной или профильной проекции цилиндра. Полученные точки соединяют плавной кривой. Затем пристраивают фигуру сечения и фигу­ру нижнего основания (окружность).

Построение развертки поверхности конуса начинают с нанесения из какой-либо точки S дуги окружно­сти радиусом, равным длине образующей конуса. На этой дуге откладывают 12 частей окружности ос­нования и полученные точки соединяют с вершиной прямьми образующими. От вершины S на прямых откладывают действительные длины отрезков образующих от вершины конуса до секущей плоскости. К развертки конической поверхности пристраивают фигуры сечения и основания конуса. Для более точ­ного построения развертки конической поверхности прямого кругового конуса центральный угол а сек­тора, представляющего эту развертку, можно посчитать по формуле a=180°*d/l, где d— диаметр ок­ружности основания конуса в мм, 1 — длина образующей конуса в мм.

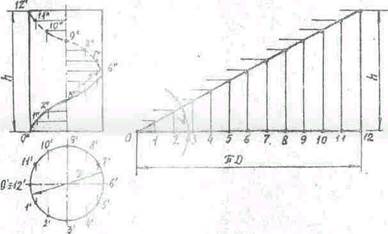
21. Цилиндрические и конические винтовые линии. Образование, основные параметры. Цилиндрические винтовые линии образуются на поверхности цилиндра вращения при равномерном перемещении точки вдоль его образующей и при одновременном равномерном вращении образующей около оси цилиндра. Проекции цилиндрической винтовой линии: (фронтальная — синусоида, горизонтальная — окружность. Фронтальная проекция строится следующим образом: делим окружность основания цилиндра и шаг винтовой линии (отрезок, на который подымается точка А при полном повороте

образующей цилиндра) на одинаковое количество частей (12). Определяем соответственные фронталь­ные проекции перемещающейся точки и соединяем их плавной кривой. При развертки цилиндрической поверхности винтовая линия является прямой. Угол а называется углом подъема винтовой линии:

tga=h/7iD, где h - шаг линии, D — диаметр цилиндра. Винтовая линия на цилиндрической поверхности имеет постоянный подъем.

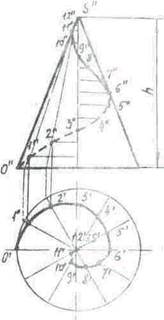
Коническая винтовая линия образуется на поверхности конуса вращения при равномерном перемещении точки вдоль его образующей и при одновременном равномерном вращении образующей около конуса. 1 проекции конической винтовой линии (горизонтальная спираль Архимеда, а фронтальная — затухающая синусоидальная кривая с уменьшающейся длиной волны) строится следующим образом: делим окружность основания конуса и шаг винтовой линии на одинаковое количество частей (12). Определяем по соответственным образующим конуса местоположение проекций точек 1,2,..., 12 и соединяем их • 1лавной кривой. Винтовые линии могут быть правыми и левыми. Правой называется винтовая линия, которая подымается слева вверх направо. Левая винтовая линия подымается справа вверх налево. Часть винтовой линии, соответствующая одному ее шагу, называется витком. Винтовые линии, образованные на цилиндре и конусе, имеют большое практическое значение в практике (используются для образования резьб). 22. Поверхности. Классификация, определитель и каркасы поверхно-.' ген.

Поверхностью называется совокупность всех последовательных положений некоторой линии, переме­щающейся в пространстве по определенному закону. Эту линию называют образующей. Перемещение образующей может быть подчинено какому-нибудь закону или быть случайным. В первом случае по­верхность называют закономерной, а во втором — незакономерной. Выделяют три способа образования поверхностей: аналитический (поверхность задается уравнением); каркасный (поверхность задается оп­ределенной совокупностью точек и линий); кинематический (поверхность рассматривается как сово­купность последовательных положений некоторой линии (образующей), перемещающейся в простран­стве по определенному закону. Совокупность геометрических элементов (форма образующей, форма направляющей, закон переме1цения образующих) и связей между ними называется определителем по­верхности. Определитель поверхности состоит из двух частей: 1) геометрическая часть определителя — совокупность постоянных геометрических элементов и соотношения между ними; 2) алгоритмическая часть определителя — закон, по которому строятся тоски и линии поверхности. В зависимости от фор­мы образующей и закону перемещения поверхности можно приблизительно разделить на группы. Ли­ нейчатые поверхности— поверхности, образующей которых является прямая линия. Линейчатые по­верхности могут быть: развертываемые поверхности, т.е. после разреза их по образующей можно со­вместить с плоскостью без разрыва и складок; неразвертываемые поверхности, т.е. их нельзя совмес­тить с плоскостью без разрывов и складок. Нелинейчатые поверхности — поверхности, образующая ко­торых является кривой линией. Нелинейчатые поверхности могут быть: с постоянной образующей — поверхности, образующая которых не изменяет своей формы в процессе образования поверхности; с переменной образующей - - поверхности, образующая которых изменяется в процессе образования по­верхности. Если представит!, себе совокупность прямолинейных образующих и совокупность образую­щих окружностей, то каждая линия одной совокупности пересечет все линии другой совокупности, в результате чего получается.кт.пкас данной поверхности.

23. Поверхности вращешш. -Эоетроение точки на поверхности вращения. Поверхности, образованные вращением линии (образующей) вокруг прямой (оси вращения), называют­ся поверхностями вращения. Определитель поверхности вращения включает образующую и ось враще­ния. При образовании поверкноети вращения каждая точка образующей описывает в пространстве ок­ружность. Эти окружности па бывают параллелями. Плоскости параллелей всегда перпендикулярны к оси вращения. Наибольшую и'; параллелей называют экватором, наименьшую —горлом поверхности. Плоскость, проходящую чсрс; ось поверхности вращения, называют меридиональной плоскостью. Ли­ния пересечения ииверхнпс i ii вращения меридиональной плоскостью называется меридианом поверх­ности. Если поверхность вращения образована вращением прямой линии, то поучаем линейчатую по­верхность, коническую или цилиндрическую. Если поверхность вращения образована вращением кри­вой линии, то получаем нелинейчатую поверхность, сферу или тор. Сфера — поверхность, образован­ная вращением окружности вокруг ее диаметра. Top — поверхность, образованная вращением окруж­ности (или ее дуги) вокруг прямой — оси вращения, размещенной в плоскости окружности и не прохо­дящей через центр окружное) ii. Top называется замкнутым, если ось вращения пересекается с окружно­стью, которая образует ею, и открытым, если ось вращения не пересекается с окружностью, которая его образует. Эллипсоид вращения образуется вращением эллипса вокруг одной из осей. Параболоид вра­щения образуется вращением параболы вокруг оси. Гиперболоид вращения образуется вращением ги­перболы вокруг оси. При вращении гиперболы вокруг мнимой оси получается однополосный гипербо­лоид вращения, а при вращс! (и и вокруг действительной оси — двуполостный гиперболоид вращения. Положение точки на поверхности вращения определяется при помощи окружности, проходящей через эту точку на поверхности нращения.

24. Линейчатые поверхности (развертываемые и неразвертываемые). Нелинейчатые поверхно­сти.

25. Построение точки ik •pi '.ч •чения прямой с поверхностью (общий случай). Способы построения точек пересечения np«Miii; с поверхностью.

^* Через прямую пронес ш вспомогательную плоскость

<•» Определить линию пересечения вспомогательной плоскости с заданной поверхностью»> Определить искомые точки (входа и выхода) как результат пересечения заданной прямой с най­денной линией перессчсня *t* Определить видим осп,