Горизонтали и фронтали плоскости. Точка и прямая в плоскости

Точка принадлежит плоскости,если она лежит на прямой, принадлежащей плоскости. Например, точка D(D',D") принадлежит плоскости АВС (A'B'C', A"B"C"), т. к. она лежит на прямой С1(С'1',С"1"). Прямая принадлежит плоскости, если две ее точки принадрежат плоскости. Прямая принадлежит плоскости,если она проходит через одну точку этой плоскости и параллельна какой-нибудь прямой, лежащей в плоскости. К числу прямых, которые занимают особое положение в плоскости, относят горизонтали и фронтали. Горизонталями плоскости называют прямые, принадлежащие плоскости и параллельные горизонтальной плоскости проекций. Фронталями плоско­сти называют прямые, принадлежащие плоскости и параллельные фронтальной плоскости проекций.

9. Взаимное положение прямой и плоскости (прямые параллельные и перпендикулярные плоско­сти). Проецирование прямого угла.

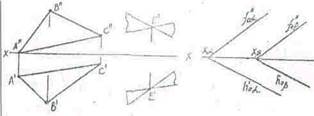
Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, принадлежащей данной плоскости. Прямая перпендикулярна к плоскости, если она перпендикулярна ко всем двум прямым, ко­торые пересекаются в этой плоскости принадлежат ей. Но, чтобы при этом проекция перпендикуляра к плоскости общего положения оказалась перпендикулярной к соответственной проекции некоторой пря­мой этой плоскости- прямая должна быть горизонталью или фронталью, или профильной прямой плос­кости. Поэтому, если надо построить перпендикуляр к плоскости, берут в общем случае две такие пря­мые. Таким образом, у перпендикуляра к плоскости его горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали, фронтальная проекция перпендикулярна к фронтальной проек­ции фронтали. Очевидно, если плоскость задана следами, мы получаем следующий результат: если прямая перпендикулярна к плоскости, то горизонтальная проекция этой прямой перпендикулярна гори­зонтальному следу плоскости, а фронтальная проекция перпендикулярна к фронтальному следу плоско­сти. Если через точку D надо провести прямую L (Г, I"), перпендикулярную к плоскости, заданой Д АВС нужно выполнить следующие построения:

1) Провести в плоскости горизонталь С1 (СТ, С"1") и фронталь А2 (А'2', А"2");

2) Через горизонтальную проекцию D' точки D провести прямую Г, перпендикулярную к горизонтальной проекции горизонтали СТ, — это будет горизонтальная проекция перпендикуляра;

3) Через фронтальную проекцию D" точки D провести прямую I", перпендикулярную к

фронтальной проекции фронтали А"2", — фронтальная проекция перпендикуляра. Построенная прямая L (Г, I") и есть перпендикуляр к плоскости Д АВС. На основании перпендикулярности прямой и плоскости можно решать следующие задачи: определять расстояние в пространстве; определять расстояние между двумя параллельными плоскостями; прово­дить плоскость, параллельную данной, находящейся на некотором расстоянии; из точки, лежащей в плоскости, строи ть перпендикуляр к ней; проводить через точку плоскость, перпендикулярную к дан­ной плоскости.

Теоретической основой для построения на чертежах проекций прямых и плоскости, перпендикулярных относительно к друг другу, служит теорема о проецировании прямого угла. В общем случае угол про­ецируется на плоскость в натуральную величину, если две его стороны параллельны этой плоскости. Прямой угол проецируется в натуральную величину, если хотя бы одна его сторона параллельна плос­кости проекций, а другие не перпендикулярны к этой плоскости. Таким образом, возможно три случая проецирования прямого угла на плоскость:

1) Если две стороны прямого угла заданы прямыми общего положения, то прямой угол проециру­ется с искажением на все три плоскости проекций;

2) Если две стороны прямого угла параллельны какой-нибудь плоскости проекций, то на эту плос­кость прямой угол проецируется в натуральную величину;

3) Если одна сторона прямого угла прямая общего положения, а другие параллельны плоскости проекций, то прямой угол проецируется на эту плоскость проекций в прямой.

10. Взаимное положение двух плоскостей. Построение линии пересечения плоскостей при раз­личных способах их задания.

Две плоскости параллельны, если две пересекающие прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Если плоскость задана следами, то параллельность определяется параллельностью соответственных

...е плоскости взаимно перпендикулярны, если одна из них содержит прямую, перпендикуляр-.ругой плоскости, или перпендикулярна к прямой, лежащей в другой плоскости.

 

Две плоскости пересекаются по прямой. В зависимости от, того какое положение занимают плоскости, возможно три случая пересечения плоскостей:

1) Две плоскости занимают частное положение. Возможно два варианта: 1) две пересекающиеся плоскости перпендикулярны к одной плоскости проекций =^> линия пересечения перпендикуляр­на к этой же плоскости проекций; 2) две пересекающиеся плоскости перпендикулярны к разным плоскостям проекций => линия пересечения есть линия, проекция которой совпадает со следами плоскостей.

2) Одна из плоскостей занимает общее положение, а другая — частное => одна проекция линии пе­ресечения совпадает со следом плоскости частного положения, а другая проекция определяется из условия принадлежности этой прямой плоскости общего положения.

3) Две плосюости занимают общее положение. Построение линии пересечения плоскостей при различных способах их задания:

•^ Провести вспомогательную плоскость, пересекающую две данных плоскости (плоскость частного положения);

•^ Определить линии пересечения вспомогательных плоскостей с каждой из данных плоско­стей;

•^ Найти точки пересечения Полученных линий и соединить их.

11. Правила построения точки пересечения прямой с плоскостью. Определение видимости пря­мой.

Правила построения точки пересечения прямой с плоскостью:

- Через прямую провести вспомогательную плоскость;

- Определить линию пересечения заданной и вспомогательной ' плоскостей;

' - Определить точку пересечения прямой с плоскостью как результат заданной прямой с найденной точкой пересечения;

- Определить видимость прямой.

Аксонометрические проекции. Основные понятия и определения. Построение окружности в аксонометрических проекциях.

| Способ аксонометрического проецирования заключается в том, что проецирующую фигуру соотносят с некоторой системой прямоугольных координат и вместе с этой системой параллельно проецируют на одну плоскость проекций. Прямые OX, OY, OZ — оси координат в пространстве, прямые ОцХ, OyY, OyZ — их проекции на

плоскость а, которые называются аксонометрическими осями. На осях X, Y, Z отложены некоторые отрезки длиной L, прини­мающиеся за единицу измерения на этих осях. Отрезки /х? 1у, 1-г. ^на аксонометрических осях есть

проекции отрезка /. Отношения l^ll, /y/Z, 1^11 называются коэффициентами искажения по аксонометри­ческим осям. Коэффициенты искажения по оси ОуХ обозначим k, по оси o(^y — m, по оси O^Z — п. В зависимости or соотношения коэффициентов искажения проекции делятся на: изометрическую (k=m=n), димегрическую (1<^пт=п), триметрическую (k^m^n). В зависимости от угла между направлени­ем проецирования и аксонометрической плоскостью аксонометрические проекции могут быть косо­угольными и прямоугольными.

13. Стандартные виды аксонометрических проекций. Коэффициенты искажения. Построение ок­ружности в аксонометрических проекциях.

ГОСТ 2.317-69 рекомендует использовать следующие аксонометрические проекции: прямоугольная изометрическая

проекция; прямоугольная диметрическая проекция; косоугольная • фронтальная диметрическая проекция; косоугольная фронтальная изометрическая проекция; косоугольная горизонтальная изометриче­ская проекция.

Прямоугольная изометрическая проекция.

Аксонометрические оси в изометрии размещены под углом 120° одна от другой, причем ось Z размещается всегда вертикально. Коэффициенты искажения по всех осях равны между собой: k=m=n,

k^nr'+ir^Sk^ => 1<70,82. Для упрощения построения принимают коэффициенты искажения равными единицы. В этом случае аксонометрическая проекция получается увеличенной в 1,22 раза относительно натуральной величины предмета. Окружность, размещенная в координатных плоскостях или плоско­стях, которые им параллельны, проецируются в виде эллипсов. Большая полуось АВ размещается пер­пендикулярно к той сои, которой нет в плоскости размещения окружности. Размеры осей эллипсов:

большая полуось — AB=l,22d; малая ось — CD=0,7d, где d — диаметр проецируемой окружности.

Прямоугольная диметрическая проекция.

В прямоугольной диметрической проекции ось Х размещается под углом 7° 10' к горизонтальной линии, ось Y под углом 41°25' к этой же линии. Ось Z — вертикально. Коэффициенты искажения по осях Х и Z равны между собой, а по оси Y=0,5, k=n; m^k. Тогда равенство k²+n-l²+n²=2k²+^L^k²=2 => k=0,94. Для построения принимают коэффициенты искажения по осях Х и Z=l, по оси Y=0,5. Построены чертеж при этом получается увеличенным в 1,06 раз. Окружности, находящиеся в координатных плоскостях, как и в изометрии,

проецируются в виде эллипсов. В плоскостях XOY и ZOY или им параллельных эллипсы по форме и размерах одинаковы. Большая ось АВ=1,06d, малая ось CD-=0,35d. В плоскости XOY большая ось AB=l,06d, малая ось CD=0,35d (d — диаметр окружности). Большая ось размещается перпендикулярно к отсутствующей оси плоскости размещения окружности.

Косоугольные аксонометрические проекции.

• "' i' •¹''.¹.'•''. •^л:•'^••^:•'.."•^\••"••••.^:'^^::.•••:'^''-.^'^'.л^м-ш^. "'•-'.• ••' ' '[Часто применяется такая косоугольная диметрия, коэффициенты искажения которой по оси Y принимаются равными 0,5, а угол между этой осью и другими осями равен 135°. Такая аксонометрия называется фронтальной диметрической проекцией. Особенностью данной проекции является то, что окружность проецируется без искажения на фронтальную плоскость проекций. 14. Способы прсобразопиннн проекций. Способ плоскопараллельного перемещения. Способы преобразования проекций: перемена плоскостей проекций; вращение вокруг проецирующей прямой; вращение вокруг линий уровня; плоскопараллельное перемещение; совмещение. Задачи: а) прямая общею положения преобразуется в прямую уровня; б) прямая уровня преобразуется в проеци­рующую прямую; в) плоскос-1 ь общего положения преобразуется в проецирующую плоскость; г) про­ецирующая плоскость преобразуется в плоскость уровня.

Способ плоскопараллельного перемещения. Сущность этого способа заключается в перемещении геометрической фигуры относительно данных плоскостей проекций в частное положение таким образом, чтобы траектория перемещения всех ее точек находилась в параллельных плоскостях. Плоскопараллельное перемещение — общий случай вращения без указания местоположения оси. При параллельным переносе геометрической фигуры относительно плоскостей проекций проекция фигуры на эту плоскость хоть и изменяет свое положение, но не изменя­ется по форме и размерах.

15. Способ замены плоское! ей.

Сущность этою способа заключается в переходе от данной системы плоскостей проекций Щ/П^ ^{к н0}"

вой. Проецируемая фигура при этом не меняет своего положения в пространстве. Одна из основных плоскостей проекций \\\ или П^ заменяется новой плоскостью, размещенной определенным образом

относительно неподвижного объекта проецирования. Поскольку в новой системе плоскостей проекций проецирование остается прямоугольным, то новая плоскость должна быть перпендикулярной к незаме­ненной плоское! и проекции Щ или П^.