Криволинейная трапеция-плоская криволинейная фигура, ограниченная отрезком оси абцисс [a,b], кривой y=f(x), где f(x) непрерывна и неотрицательна на этом отрезке, и 2мя прямыми x=a,x=b. Если ф-я незнакопостоянна, то определнный интеграл численно равен алгоритму суммы S криволинейной трапеции, лежащей над и под осью ox. В эту сумму S крив. Трап., леж. Над осью входят со знаком +, а под ней- со знаком -.
Площадь S, ограниченная непрерывными кривыми y=f1(x), y=f2(x), вертикалями x=a, x=b, где f1(x)≤ f2(x) при a≤x≤:
S= 
Объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной кривой y=f(x)≥0 и прямыми x=a, x=b (a<b), y=0:
=
Объем тела, образованного вращением вокруг оси Oy криволинейной трапеции, ограниченной кривой x=g(y)≥0 и прямыми y=a, y=b (a<b), x=0: V = 
Несобственные интегралы первого и второго рода.
1)
Пусть f(x) опред на [a;+∞) и интегрируема в любой конечной его части [a;R] так, что существует определенный интеграл
∃ 
Если при R→+∞ для этого интеграла существует определенный конечный предел, то его называют несобственным интегралом ф-ии f(x) в промежутке [a;+∞).
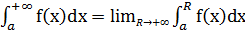(1)- несобственный интеграл 1ого порядка
При интегрировании говорят, что интеграл существует, те сходится, если lim бесконечен или не существует, то про интеграл говорят, что он не существует или расходится
- при условии, что оба интеграла сходятся
2)
Несобственный интеграл от неограниченной ф-ии
f(x) опр. [a,b)
(∙)x=b-особ. (∙), если ф-я неограниченна в любой окрестности этой (∙), но ограничена на любом отрезке [a,b-𝜇], заключенном в [a,b).
Пусть на любом отрезке[a,b-𝜇] ф-я интегрируема, те существуетопределенный интеграл
∃ 
, ∀𝜇>0, b-𝜇>a
Если для интеграла при 𝜇→0 существует конечный lim, то его называют интегралом 2ого порядка.
Если 
есть, то интеграл существует (сходится), если нет, то расходится.
Признаки сходимости для несобственных интегралов первого и второго родов.
1)признак сравнения несобственных инт.
a)f(x)g(x)- неопред. [a,+∞)
0≤ f(x)≤ g(x)
2)если f(x)g(x)—неотрицательные ф-ии и существует конечный предел их отношения при x→+∞,то несобственные интегралы
сходятся и расходятся одновременно
3)частный признак сравнения.
Если x→+∞ неопр. ф-я f(x) является б.малой порядка 𝛾(𝛾>0), то 
сходится при 𝛾>1 и расходится при 𝛾≤1.
2.Если ф-я определена для всех x≥a и 
то 
сходится абсолютно. Если сходится условно, то 
Дифференциальное уравнение и его решение. Примеры. Формулировка теоремы о существовании и единственности решения дифференциального уоавнения первого порядка с геометрической интерпретацией.
ДУ- ур-е, в котором неизвестная ф-я или вектор-ф-я входит под знаком производной или дифференциала.
1)Обыкновенные ДУ, в котором неизвестные являются ф-ей 1ой переменной
2)ДУ в частных производных, в которых неизвестные ф-ии являются ф-ями 2х и более переменных.
Порядок ДУ- порядок старшей входящей в ДУ неизвестной ф-ии.
Решением обыкновенного ДУ n-ого порядка, те ур-я вида
F(x, y(x),y’(x), y''(x),…, y(n)(x))=0
называется ф-я y=𝜑(x),которая при подстановке в ДУ обращает его в тождество.
График решения ДУ называется интегральной кривой.
Решение ДУ- интегрирование ДУ. Задача интегрирование- нахождение всех решении этого ур-я и изучении их св-в.
ДУ 1ого порядка- ур-е вида F(x, y, y’)=0, где x- независимая переменная, y- искомая ф-я, y'- ее производная.
Если его можно разрешить относительно y', то y'= dy/dx =f(x,y)- ур-е 1ого порядка, разрешенное относительно производной.
P(x,y)dx+Q(x,y)dy=0.
Теорема Коши (Теорема о существованиии единственности решения ДУ 1ого порядка)
Если ф-я f(x,y) и ее частная приизводня f'y(x,y) определены и непрерывны в некоторой области G плоскости oxy, то какова бы не была внутренняя точка (x0, y0) области G, в некоторой окрестности этой точки существует единственное решение ур-я y'= f(x,y), удовлетворяющее условиям y=y0, x=x0
Геометрически теорема утверждает, что через каждую внутреннюю точку (y0, x0) области G проходит единственная интегральная кривая.
