Условный экстремум функции нескольких переменных. Определение и методы вычисления на примерах.
Точка М(хо,уо) называется точкой условного max (min) ф-и z=f(x,y), при условии g(x,y)=C, если сущ-ет такая окрестность этой точки, что во всех точках (х,у) из этой окрестности, удовлетворяющих условию g(x,y)=C, выполняется неравенство 
.
Уравнение g(x,y)=C называется уравнением связи.
Метод множителей Лагранжа основан на том, что точка условного экстремума (xо,yо) ф-и z=f(x,y) при условии g(x,y)=C соответствует точке экстремума (xo,yo,λo) ф-и L(x,y,λ)=f(x,y)+λ[g(x,y) – C]. Ф-я L называется ф-ей Лагранжа, а λ – множителем Лагранжа.
Например, 
Первообразная функция и неопределенный интеграл. Таблица основных интегралов.
Ф-я F(x) в данном промежутке называется первообразной для ф-ии f(x), если во всем этом промежутке f(x) явл производной для ф-ии F(x): F’(x)=f(x).
Если в некотором конечном (или бесконечном), замкнутом (или нет) промежутке Х ф-я F(x) явл первообразная для f(x), то и ф-я F(x)+C, где С-const. так же будет первообразной для f(x).
Каждая ф-я, первообразная для f(x), в промежутке Х может быть представлена в форме F(x)+C.
Совокупность всех первообразных для f(x) на промежутке Х называется неопределенным интегралом от f(x) и обозначается 
.
f(x) – подынтегральная ф-я
Таблица основных интегралов
| 1) |  =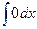
| С | 10) |  =
| –ctg x+C |
| 2) |  =
| x+C | 11) |  =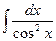
| tg x+C |
| 3) |  =
| 
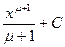
| 12) |  =
| 
|
| 4) |  =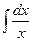
| 
| 13) |  =
| sh x+C |
| 5) |  =
| 
| 14) |  =
| ch x+C |
| 6) |  =
| 
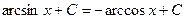
| 15) |  =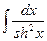
| –cth x+C |
| 7) |  =
| 
| 16) |  =
| th x+C |
| 8) |  =
| –cos x+C | 17) |  =
| ex+C |
| 9) |  =
| sin x+C |
Вычисление интегралов с помощью использования таблицы простейших интегралов, основных свойств и правил называется интегрированием.
Свойства неопределенного интеграла с доказательством и простейшие правила интегрирования.
Свойства:
1) 
2) 
3) 
Правила:
1) С – const (C не равно 0) 
2) 
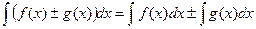
3) 
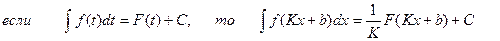
Вычисление интегралов с помощью использования таблицы простейших интегралов, основных свойств и правил называется интегрированием.
Метод замены переменных при интегрировании с демонстрацией на конкретных примерах.
Метод замены переменной (метод подстановки) – один из основных методов интегрирования, описываемый следующей формулой: 
, где ф-я x=φ(t) имеет непрерывную производную на рассматриваемом промежутке.
Новую переменную можно не вписывать явно (в таких случаях говорят о преобразовании ф-и под знаком дифференциала или о введении постоянных и переменных под знак дифференциала).
Интегрирование путем замены переменной в неопределенном интеграле производится с помощью подстановок 2х видов:
1) x=φ(t), где φ(t) – монотонная непрерывная дифференцируемая ф-я новой переменной t.
dx=φ’(t)dt, 
2) t=ψ(x), 
Замечание. При выборе подстановки t=ψ(x), упрощающей подынтегральное выражение, нужно помнить, что в его составе должен найтись множитель ψ’(x)dx, дающий дифференциал новой переменной dt: ψ’(x)dx=dt.
Например:
1. 
2.
3.
