Модуль №1. Элементы линейной алгебры и аналитической геометрии.
Тема 1.4. Элементы аналитической геометрии в пространстве и на плоскости.
Учебные вопросы:
1. Прямая на плоскости.
2. Кривые второго порядка.
Прямая на плоскости.
Среди различных уравнений прямой на плоскости наиболее распространенными можно считать следующие.
Общее уравнение прямой на плоскости имеет вид
 ,
,  (1.1)
(1.1)
где A, B, C – вещественные числа (неравенство  означает, что коэффициенты A и B не обращаются в нуль одновременно). Вектор
означает, что коэффициенты A и B не обращаются в нуль одновременно). Вектор  называется вектором нормали и перпендикулярен данной прямой.
называется вектором нормали и перпендикулярен данной прямой.
Уравнение прямой с угловым коэффициентом представляет собой уравнение, разрешенное относительно y:
 . (1.2)
. (1.2)
Здесь k – угловой коэффициент прямой (тангенс угла, который прямая образует с положительным направление оси OX).
Уравнение прямой в отрезках записывается в виде
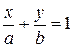 , (1.3)
, (1.3)
где a и b – соответствующие координаты точек пересечения прямой с осью OX (точка A(a;0)) и OY (точка B(0;b)).
Например, прямая  проходит через точки A(1;0) и B(0;-2); прямая
проходит через точки A(1;0) и B(0;-2); прямая  через точки A(1/3;0) и B(0;1/5); (так как уравнение
через точки A(1/3;0) и B(0;1/5); (так как уравнение  равносильно уравнению
равносильно уравнению  .
.
Каноническое уравнение прямой имеет вид 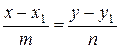 , а параметрическое –
, а параметрическое –
 , (1.4)
, (1.4)
где 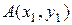 - точка, лежащая на прямой, а
- точка, лежащая на прямой, а  - направляющий вектор прямой.
- направляющий вектор прямой.
Пример 1.1. Дана прямая  . Выписать ее вектор нормали, найти угловой коэффициент, построить прямую на плоскости.
. Выписать ее вектор нормали, найти угловой коэффициент, построить прямую на плоскости.
Решение. Сравнивая уравнение данной прямой с (1.2), замечаем, что в нашем случае  (коэффициент при x),
(коэффициент при x),  (коэффициент при y), поэтому
(коэффициент при y), поэтому  . Чтобы найти угловой коэффициент, исходное уравнение необходимо разрешить относительно y:
. Чтобы найти угловой коэффициент, исходное уравнение необходимо разрешить относительно y:
 ;
; 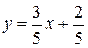 . (1.5)
. (1.5)
Сравнивая с уравнением (1.2), замечаем, что k=3/5. Как известно, для построения прямой необходимо знать координаты двух точек, через которые проходит прямая. Задавая значения x, из (1.5) можно найти соответствующие значения y:  ;
;  . Итак, остается провести прямую, проходящую через точки A(0; 2/5), B(1; 1).
. Итак, остается провести прямую, проходящую через точки A(0; 2/5), B(1; 1).
Пример 1.2. Прямая задана параметрическим уравнением  . Выписать направляющий вектор данной прямой и координаты двух точек, лежащих на ней, а также координаты ее вектора нормали.
. Выписать направляющий вектор данной прямой и координаты двух точек, лежащих на ней, а также координаты ее вектора нормали.
Решение. В соответствии с уравнением (1.4)  , а точка A(-2;0) лежит на прямой. Чтобы найти координаты второй точки, лежащей на прямой, зададим какое-нибудь значение параметра t. В частности, при t=1 x=-1, y=-3, т.е. точка B(-1;-3) принадлежит прямой. Вектор нормали связан с общим уравнением прямой, а чтобы перейти к нему, необходимо в одном из заданных уравнений выразить t через x и полученное выражение подставить во второе уравнение. Например, из первого уравнения
, а точка A(-2;0) лежит на прямой. Чтобы найти координаты второй точки, лежащей на прямой, зададим какое-нибудь значение параметра t. В частности, при t=1 x=-1, y=-3, т.е. точка B(-1;-3) принадлежит прямой. Вектор нормали связан с общим уравнением прямой, а чтобы перейти к нему, необходимо в одном из заданных уравнений выразить t через x и полученное выражение подставить во второе уравнение. Например, из первого уравнения 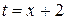 , поэтому
, поэтому  . Окончательно имеем:
. Окончательно имеем:  ,
, 
Пример 1.3. Привести к уравнению в отрезках прямую, заданную общим уравнением  .
.
Решение. Проведем преобразования общего уравнения, чтобы привести его к виду (1.3).
 .
.
Последнее уравнение и есть искомое уравнение в отрезках.
Угол j между прямыми, заданными уравнениями с угловым коэффициентом ( ,
, 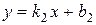 ), определяется с помощью формулы
), определяется с помощью формулы
 . (1.6)
. (1.6)
Из (1.6) вытекают условия параллельности (  ) и перпендикулярности двух прямых (
) и перпендикулярности двух прямых ( ).
).
Пример 1.4. Выбрать из прямых (I) – (V) параллельные и перпендикулярные, определить угол между прямыми (I) и (VI):
(I)  ; (II)
; (II)  ; (III)
; (III) 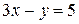 ;
;
(IV)  ; (V)
; (V)  ; (VI)
; (VI) 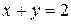 .
.
Решение. Сначала для каждой прямой найдем угловой коэффициент:
(I):  ;
;
(II): 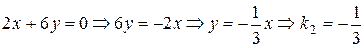 ;
;
(III) 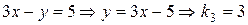 ;
;
(IV) 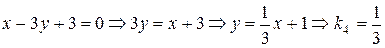 ;
;
(V)  ;
;
(VI)  .
.
Поскольку 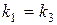 ,
,  , получаем, что прямые (I) и (III), (II) и (V) параллельны. С другой стороны,
, получаем, что прямые (I) и (III), (II) и (V) параллельны. С другой стороны,  , а потому прямые (I) и (II) перпендикулярны (следовательно, перпендикулярны и прямые (III) и (II), (I) и (V), (III) и (V)). Чтобы найти тангенс угла между прямыми (I) и (VI), воспользуемся формулой (8):
, а потому прямые (I) и (II) перпендикулярны (следовательно, перпендикулярны и прямые (III) и (II), (I) и (V), (III) и (V)). Чтобы найти тангенс угла между прямыми (I) и (VI), воспользуемся формулой (8):  . Но тогда
. Но тогда 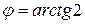 .
.
Составление уравнений прямых. Рассмотрим основные типы возникающих задач.
1) Записать уравнение прямой с известным угловым коэффициентом  , проходящей через заданную точку
, проходящей через заданную точку 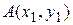 . Ответом является уравнение
. Ответом является уравнение
 . (1.7)
. (1.7)
Пример 5. Составить уравнение прямой, проходящей через точку A(2,-3) и образующей с положительным направлением оси OX угол 1200.
Решение. Координаты точки известны, а угловой коэффициент  - это тангенс угла наклона, т.е.
- это тангенс угла наклона, т.е.  . Подставляя в (1.7), получаем:
. Подставляя в (1.7), получаем: 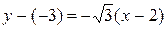 или
или  .
.
2) Записать уравнение прямой, проходящей через заданную точку 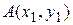 параллельно прямой
параллельно прямой  . Для решения используем уравнение (1.7) и учтем, что угловые коэффициенты параллельных прямых совпадают:
. Для решения используем уравнение (1.7) и учтем, что угловые коэффициенты параллельных прямых совпадают:
 . (1.8)
. (1.8)
3) Записать уравнение прямой, проходящей через заданную точку 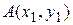 перпендикулярно прямой
перпендикулярно прямой  . Угловые коэффициенты перпендикулярных прямых связаны соотношением
. Угловые коэффициенты перпендикулярных прямых связаны соотношением  , поэтому
, поэтому 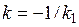 . Остается подставить это в (1.8) и получить уравнение:
. Остается подставить это в (1.8) и получить уравнение:
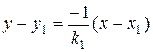 . (1.9)
. (1.9)
Пример 6. Составить уравнения прямых, проходящих через точку
A(2,-3) параллельно и перпендикулярно прямой  .
.
Решение. Так как  , то угловой коэффициента данной прямой
, то угловой коэффициента данной прямой  . Чтобы составить уравнение прямой, проходящей через A(2,-3) параллельно данной прямой, воспользуемся уравнением (1.8):
. Чтобы составить уравнение прямой, проходящей через A(2,-3) параллельно данной прямой, воспользуемся уравнением (1.8):  или
или  . Результат можно проверить, подставив в полученное выражение координаты заданной точки:
. Результат можно проверить, подставив в полученное выражение координаты заданной точки:  (если получили тождество, как в данном примере, уравнение правильное).
(если получили тождество, как в данном примере, уравнение правильное).
Аналогично действуем при составлении уравнения перпендикулярной прямой, только используем (1.9):  ,
,  , и окончательно
, и окончательно  . Проверка:
. Проверка:  .
.
4) Уравнение прямой, проходящей через две заданные точки  ,
,  , имеет вид
, имеет вид
 . (1.10)
. (1.10)
Пример 7. Написать уравнение прямой, проходящей через точки A(3;3), B(-1;5).
Решение. Подставляя в (1.10) координаты данных точек, получаем:
 .
.
Собирая теперь все в одну сторону, приходим к уравнению  . Проверить результат можно, подставляя в него поочередно координаты точек (как при проверка в примере 6):
. Проверить результат можно, подставляя в него поочередно координаты точек (как при проверка в примере 6):  ,
,  .
.
Замечание. В некоторых задачах нужно найти точку пересечения заданных прямых. Для этого решают систему уравнений, задающих эти прямые.
Пример 8. В треугольнике с вершинами O(0;0), A(3;3), B(-1;5) найти уравнения стороны AB, медианы AE и высоты OK, а также длину высоты OK.
Решение. Уравнения стороны AB было получено при решении примера 6: 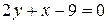 .Далее, по определению медианы треугольника точка E – середина отрезка BO, поэтому ее координаты можно найти по формуле (1.3):
.Далее, по определению медианы треугольника точка E – середина отрезка BO, поэтому ее координаты можно найти по формуле (1.3):
 ,
,  .
.
Таким образом, теперь надо составить уравнение прямой, проходящей через точки A(3;3) и E(-1/2;5/2). Подставляем их координаты в (1.10):
 .
.
Итак, уравнение медианы AE имеет вид  .
.
Далее, высота OK – это прямая, проходящая через вершину O перпендикулярно прямой AB. Воспользуемся уравнением (11). Угловой коэффициент  прямой AB находим из уравнения
прямой AB находим из уравнения  :
:  , поэтому
, поэтому  . Тогда имеем:
. Тогда имеем:  , и уравнение высоты OK
, и уравнение высоты OK  .
.
Теперь найдем координаты K – точки пересечения построенной высоты и прямой AB. Решаем систему уравнений:
 .
.
Итак,  . В силу (2.1b)
. В силу (2.1b) 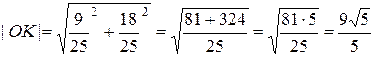 .
.
Кривые второго порядка
Определение 2.1. Всякая линия, которая в некоторой системе координат описывается уравнением второй степени относительно переменных х и у, называется кривой второго порядка.
В самом общем виде уравнение кривой второго порядка таково:
 (2.1)
(2.1)
где А, В, С, D, E, F — действительные числа, причём А, В, С одновременно не равны нулю.
Рассмотрим, прежде всего, конкретные виды кривых второго порядка и уже затем вернемся к уравнению (2.1).
ЭЛЛИПС. ВЫВОД УРАВНЕНИЯ
И ИССЛЕДОВАНИЕ ФОРМЫ
Определение 2.2. Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2 a.
Для вывода уравнения эллипса введем систему координат: ось абсцисс проведем через фокусы  и
и  , а ось ординат ‒ перпендикулярно оси абсцисс через середину расстояния между ними. Обозначим через 2с ‒ расстояние между фокусами. Тогда (рис. 1) фокусы имеют координаты
, а ось ординат ‒ перпендикулярно оси абсцисс через середину расстояния между ними. Обозначим через 2с ‒ расстояние между фокусами. Тогда (рис. 1) фокусы имеют координаты  . Пусть
. Пусть  ‒текущая точка эллипса.
‒текущая точка эллипса.
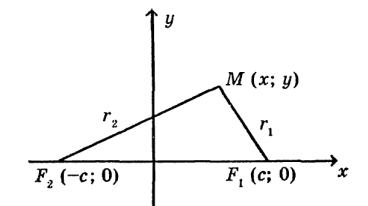
Рис. 1
Расстояние 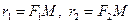 называются радиусами- векторами точки и вычисляются очень просто:
называются радиусами- векторами точки и вычисляются очень просто:
 ,
, 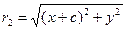 (2.2)
(2.2)
Из определения эллипса следует, что
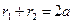 , (2.3)
, (2.3)
а простой подсчет показывает, что
 (2.4)
(2.4)
Разделив (2.4) на (2.3), имеем:
 . (2.5)
. (2.5)
Складываем и вычитаем (2.3) с (2.5). Результатом являются формулы, связывающие радиус-векторы текущей точки эллипса с ее абсциссой и заданными параметрами:
 (2.6)
(2.6)
Приравнивая 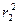 в формулах (2.2) и (2.6), имеем:
в формулах (2.2) и (2.6), имеем:
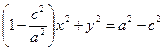 (2.7)
(2.7)
Из условия 2а > 2с (сумма длин двух сторон треугольника больше длины третьей стороны) следует, что а > с, разность  - положительна. Обозначив
- положительна. Обозначив  , получаем из (2.7):
, получаем из (2.7):
 .
.
После деления обеих частей равенства на  , приходим к каноническому уравнению эллипса
, приходим к каноническому уравнению эллипса
 (2.8)
(2.8)
Исследование формы и построение эллипса.
1) Если точка (х; у) лежит на эллипсе, то точка (х; -у) тоже лежит на эллипсе. Это означает, что эллипс симметричен относительно оси абсцисс. Аналогично показывается, что эллипс симметричен и относительно оси ординат.
2) Находим точки пересечения эллипса с координатными осями: при у = 0 имеем  . Значит, эллипс пересекает ось абсцисс в точках
. Значит, эллипс пересекает ось абсцисс в точках 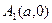 и
и  . Эти точки называются вершинами эллипса. Если х = 0, то
. Эти точки называются вершинами эллипса. Если х = 0, то  , и мы отмечаем еще две вершины эллипса
, и мы отмечаем еще две вершины эллипса 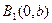 и
и  .
.
3) Выражая из уравнения эллипса у явно через х, получаем  . Область определения этой функции
. Область определения этой функции  , т. е. эллипс не выходит за пределы этой полосы. Рассуждая подобным образом, увидим, что эллипс не выходит и за пределы полосы
, т. е. эллипс не выходит за пределы этой полосы. Рассуждая подобным образом, увидим, что эллипс не выходит и за пределы полосы  . Значит, весь эллипс находится в прямоугольнике
. Значит, весь эллипс находится в прямоугольнике 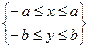 .
.
4) В первом квадранте  . Из этого равенства следует, что с увеличением х от 0 до а, у убывает от b до 0.
. Из этого равенства следует, что с увеличением х от 0 до а, у убывает от b до 0.
Принимая во внимание все сказанное, делаем вывод о форме эллипса (рис. 2). Механически эллипс можно построить таким образом: нить длиной 2а закрепить в фокусах  и
и  , в точку М поместить острие карандаша и, натянув нить, описать точкой М эллипс.
, в точку М поместить острие карандаша и, натянув нить, описать точкой М эллипс.
Полагая в каноническом уравнении эллипса  , получаем окружность радиуса а с центром в начале координат. Значит, окружность ‒частный случай эллипса.
, получаем окружность радиуса а с центром в начале координат. Значит, окружность ‒частный случай эллипса.

Рис. 2
ЭКСЦЕНТРИСИТЕТ ЭЛЛИПСА
Определение. Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большой оси
 .
.
Из равенства  или
или 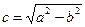 следуют два важных соотношения
следуют два важных соотношения
 и
и  ,
,
которые показывают, что эксцентриситет эллипса характеризует степень сжатия (растяжения) эллипса вдоль оси Оу: чем меньше  , тем больше отношение
, тем больше отношение  и, значит, эллипс более вытянут вдоль оси Оу; минимальное значение эксцентриситета
и, значит, эллипс более вытянут вдоль оси Оу; минимальное значение эксцентриситета  соответствует тому, что
соответствует тому, что  , т. е. равенство нулю эксцентриситета отвечает случаю окружности. Формулы (2.6) позволяют установить связь радиусов-векторов текущей точки с эксцентриситетом:
, т. е. равенство нулю эксцентриситета отвечает случаю окружности. Формулы (2.6) позволяют установить связь радиусов-векторов текущей точки с эксцентриситетом:
 . (2.9)
. (2.9)
ГИПЕРБОЛА. ВЫВОД УРАВНЕНИЯ
Определение. Гиперболой называется геометрическое место точек, для каждой из которых разность расстояний до двух данных точек, называемых фокусами, есть величина постоянная, равная 2 а.
ВЫВОД УРАВНЕНИЯ
Систему координат выбираем, как и в предыдущем случае (при выводе уравнения эллипса). Фокусы имеют те же координаты:  , но теперь 2с>2 а (длина любой их сторон треугольника больше разности длин двух других сторон) и через
, но теперь 2с>2 а (длина любой их сторон треугольника больше разности длин двух других сторон) и через  обозначим величину
обозначим величину  .
.
Далее, для текущей точки гиперболы, расположенной справа от оси Оу, имеем (рис.3):

Рис. 3
 ,
, 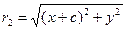 .
.

И тогда

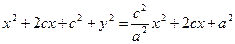

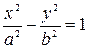 (2.10)
(2.10)
Получили каноническое уравнение гиперболы.
Этому же уравнению удовлетворяют координаты любой точки гиперболы, расположенной слева от оси ординат.
ИССЛЕДОВАНИЕ ФОРМЫ ГИПЕРБОЛЫ
1) Если точка (х; у) лежит на гиперболе, то на гиперболе лежат точки (-х; у)и (х; -у) и (-х; -у). Это значит, что обе координатные оси являются осями симметрии, а начало координат ‒ центром симметрии гиперболы или просто ее центром. Ось абсцисс называется фокальной осью гиперболы (или действительной осью).
2) Находим точки пересечения гиперболы с осями координат. При у = 0 получаем  . Точки
. Точки 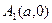 и
и  называются действительными вершинами гиперболы. Если х = 0, то
называются действительными вершинами гиперболы. Если х = 0, то  . Это означает, что гипербола не имеет точек пересечения с осью Оу; тем не менее точки
. Это означает, что гипербола не имеет точек пересечения с осью Оу; тем не менее точки 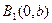 и
и  имеют большое значение для построения гиперболы. Их называют мнимыми вершинами гиперболы.
имеют большое значение для построения гиперболы. Их называют мнимыми вершинами гиперболы.
3) Выразим у явно через х:  . Эта функция определена тогда и только тогда, когда
. Эта функция определена тогда и только тогда, когда  , т. е. для
, т. е. для  и для
и для  . Это говорит о том, что гипербола имеет две ветви: левую и правую.
. Это говорит о том, что гипербола имеет две ветви: левую и правую.
4) В первом квадранте  . Когда
. Когда  то,
то,  , возрастая.
, возрастая.
5) Прямая  является асимптотой гиперболы. Действительно,
является асимптотой гиперболы. Действительно,

Из соображений симметрии следует, что прямая  тоже является асимптотой гиперболы.
тоже является асимптотой гиперболы.
ПОСТРОЕНИЕ ГИПЕРБОЛЫ
Прежде всего, построим асимптоты гиперболы. С этой целью изобразим прямоугольник со сторонами 2 а и 2 b (рис. 4).

Рис. 4
Диагонали этого прямоугольника и есть асимптоты. Теперь в первом квадранте от вершины А1 график гиперболы возрастая стремится к  , приближаясь к асимптоте. В остальных квадрантах график гиперболы строится на основе симметрии.
, приближаясь к асимптоте. В остальных квадрантах график гиперболы строится на основе симметрии.
Если  , гипербола называется равнобочной.
, гипербола называется равнобочной.
Эксцентриситетом гиперболы называется отношение фокусного расстояния
к длине действительной оси:

Т. к. с > а, то  (в отличие от эксцентриситета эллипса).
(в отличие от эксцентриситета эллипса).
Из соотношения  следует, что
следует, что
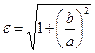 и
и  ,
,
откуда ясно, что эксцентриситет характеризует степень сжатия (растяжения) гиперболы вдоль оси Оу.
ПАРАБОЛА. ВЫВОД УРАВНЕНИЯ
Параболой называется геометрическое место точек, одинаково удаленных от данной прямой, называемой директрисой и от данной точки, называемой фокусом.
Для составления уравнения параболы выбираем систему координат: ось абсцисс проводим через фокус  перпендикулярно директрисе, ось ординат ‒ перпендикулярно оси Ох через середину расстояния р между фокусом и директрисой (рис. 5).
перпендикулярно директрисе, ось ординат ‒ перпендикулярно оси Ох через середину расстояния р между фокусом и директрисой (рис. 5).

Рис. 5
Величина р называется параметром параболы.
Пусть М(х; у) ‒текущая точка параболы,  ‒ ее фокус,
‒ ее фокус,  ‒ основание перпендикуляра, опущенного из точки М на директрису. Тогда
‒ основание перпендикуляра, опущенного из точки М на директрису. Тогда
 .
.
По определению параболы
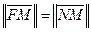
т. е.
 .
.
Отсюда

т. е.
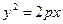 , (2.11)
, (2.11)
Это и есть каноническое уравнение параболы.
ИССЛЕДОВАНИЕ ФОРМЫ И ПОСТРОЕНИЕ ПАРАБОЛЫ
1) Если точка (х; у) лежит на параболе, то точка (х; -у) тоже лежит на параболе. Значит, парабола симметрична относительно оси Ох, т. е. ось Ох ‒ ось симметрии параболы.
2)О(0; 0) ‒ единственная точка пересечения параболы с координатными осями. Эта точка называется вершиной параболы.
3) Выразив у явным образом через х, имеем:
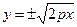 .
.
Учитывая, что р > 0, делаем вывод, что область определения параболы:  . Это говорит о том, что парабола целиком расположена в правой полуплоскости.
. Это говорит о том, что парабола целиком расположена в правой полуплоскости.
4) Формула  (верхняя часть параболы) говорит о том, что с ростом х: от 0 до
(верхняя часть параболы) говорит о том, что с ростом х: от 0 до  у тоже растет от 0 до
у тоже растет от 0 до  . Парабола имеет вид, изображенный на рис. 5.
. Парабола имеет вид, изображенный на рис. 5.






