 Рисунок 1. Рисунок 1.
|
На рисунке 1 изображены две кривые (1) и (2): y = f1(x) и y = f2(x) и общая касательная t к ним в точке A(x0; y0). Таким образом, в точке A имеем:
f '1(x0) = f '2(x0)
Пусть KM - перпендикуляр к касательной t, опущенный из произвольной, но достаточно близкой к A точки K кривой (1), а L - почка пересечения этого перпендикуляра с кривой (2). Из рисунка 1 видно, что KM > KL, т.е. что вблизи точки A кривая (1) больше отклоняется от касательной t, чем кривая (2).
Представим себе, что из точки A(x0; y0) выходит подвижная точка, которая может перемещаться или по кривой (1), или по кривой (2) в направлении возрастания аргумента x.
Из рисунка 1 видно, что когда точка движется по кривой (1), то угол a наклона касательной к кривой (1) изменяется быстрее, чем угол b, когда она движется по кривой (2).
Таким образом, из геометрических соображений ясно, что "искривленность", или "изогнутость", или, как принято говорить, кривизна кривой y = f(x) в точке A зависит от скорости изменения касательной в точке A, т.е. от скорости изменения производной f '(x) в точке A.
Но, как известно, скорость изменения производной f '1(x) в точке A(x0; y0) характеризуется значением второй производной f ''1(x) в этой точке, т.е. значением f ''1(x0), подобно тому, как скорость изменения функции f1(x) в точке A характеризуется значением f '1(x) (следует из понятия производной).
Кривые y = f1(x) и y = f2(x) имеют общую касательную t в точке A(x0; y0), т.е. в этой точке
f '1(x0) = f '2(x0)
Если бы в точке A кривые y = f1(x) и y = f2(x) имели одинаковую кривизну, то, согласно сказанному выше, и вторые производные данных функций должны были бы иметь в этой точке одинаковые значения, т.е. должно было бы выполнятся также равенство
f ''1(x0) = f ''2(x0)
Таким образом, кривизна кривой y = f(x) в какой либо точке зависит от значений первой и второй производных f '(x) и f ''(x) в этой точке.
Для того, чтобы выразить кривизну кривой y = f(x) в данной точке A(x0; y0) числом, можно, отправляясь от наглядных геометрических представлений, принять за основу следующие два положения.
I. Окружность имеет одинаковую кривизну во всех своих точках.
II. Кривизна окружности обратно пропорциональна ее радиусу R (чем меньше радиус окружности, тем больше она "искривлена"), следовательно, если обозначить через K кривизну окружности, то в любой точке окружности

Выше было установлено, что если две функции y = f1(x) и y = f2(x) в общей точке A(x0; y0) кривых y = f1(x) и y = f2(x) имеют одинаковые первые и вторые производные, т.е. если
f '1(x0) = f '2(x0) и f ''1(x0) = f ''2(x0),
то эти кривые имеют одинаковую кривизну в точке A.
|
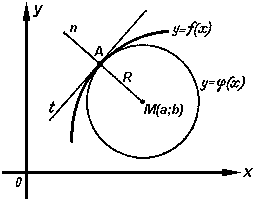
Так как кривизна окружности выражена числом, то за величину кривизны кривой y = f(x) в точке A(x0; y0) следует принять кривизну окружности, проходящей через точку A и имеющей в этой точке общую касательную с кривой y = f(x) и одинаковое направление выпуклости. Следовательно центр этой окружности должен лежать на нормали n к кривой в точке A (смотри Рисунок 2).
О п р е д е л е н и е. Окружность, проходящая через точку A и имеющая с данной кривой в этой точке общую касательную и одинаковое направление выпуклости, называется кругом кривизны кривой y = f(x) в ее точке A. Центр круга кривизны в точке A называется центром кривизны кривой y = f(x) в этой точке.
Найдем радиус R круга кривизны, а следовательно, и кривизну  данной кривой в данной точке.
данной кривой в данной точке.
Пусть
(x - a)2 + (y - b)2 = R2 (1)
- уравнение круга кривизны. Дифференцируя дважды это уравнение, находим
2(x - a) + 2(y - b)y' = 0
откуда
 (2)
(2)
Далее,
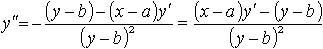 (3)
(3)
Из уравнения (2) имеем
x - a = -y'(y - b) (4)
Подставляем в уравнение (3) -y'(y - b) вместо (x - a):
 .
.
Отсюда
 (5)
(5)
Заменяя (y - b) в выражении (4) на  , будем иметь
, будем иметь
 (6)
(6)
Подставляя в уравнение (1) вместо (- a) и (- b) их выражения из (5) и (6), получим

откуда

Итак,
 (7)
(7)
Следовательно, кривизна K кривой y = f (x) в точке A(x0; y0) равна
 (8)
(8)
Но в точке x0 первые и вторые производные функций (x - a)2 + (y - b)2 = R2 и y = f(x) должны быть равны, т.е. y'0 = f '(x0), y''0 = f ''(x0), поэтому кривизна кривой y = f(x), равная кривизне окружности в точке A, будет равна







