РОЗДІЛ ІІІ. Аналітична геометрія

ЗАДАЧІ І ВПРАВИ ДЛЯ САМОСТІЙНОЇ РОБОТИ

ВИЩА МАТЕМАТИКА

ТЕМА 1. ЕЛЕМЕНТИ ЛІНІЙНОЇ АЛГЕБРИ І АНАЛІТИЧНОЇ ГЕОМЕТРІЇ

РОЗДІЛ І. Матриці. Визначники матриці. Системи рівнянь першого степеня.

Обчислити визначники

 

 

 

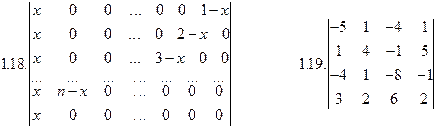
Розв`язати системи по правилу Крамера.

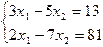
1.27.	1.30.
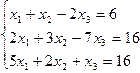
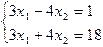
1.28.	1.31
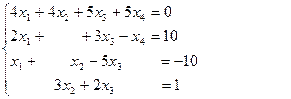
1.29.	1.32.

 

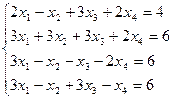
Розв`язати системи методом Гауса

(метод послідовного виключення невідомих)

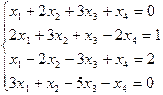
1.33.	1.34.
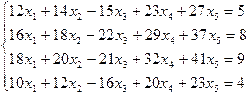
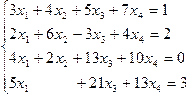
1.35.	1.36.
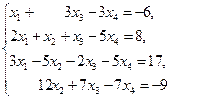
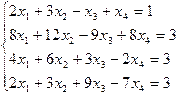
1.37.	1.38.

Обчислити ранг матриць з допомогою елементарних перетворень

1.47.	1.48.
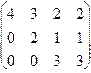
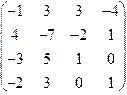
1.49.	1.50

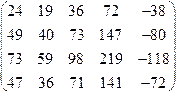
Обчислити ранг матриць методом облямування

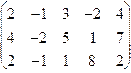
1.51.	1.52.
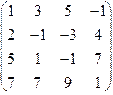
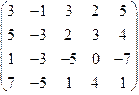
1.53.	1.54.
1.55.	1.56.
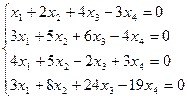
1.57.	1.58.
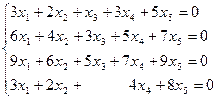
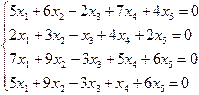
1.59.	1.60

 

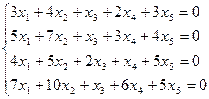
1.63. Знайти добуток 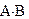на добуток 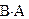двох матриць

1.64. Знайти добуток матриць А×В

1.65. Знайти добуток матриць АВ і ВА, якщо

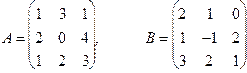
1.66. Знайти значення матричного многочлена

2А²+3А+5Е при 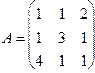, якщо Е - одинична матриця третього порядку.

 

Знайти обернені матриці

1.75. 1.76. 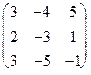1.77.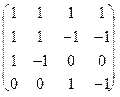

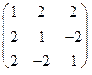1.78. 1.79. 1.80.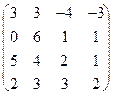

Розв’язати матричнi рiвняння

1.81. 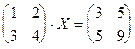1.82.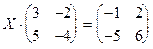

1.83. 1.84.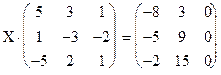

Розв’язати системи, представивши їх у вигляді матричних рівнянь

1.85. 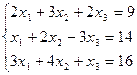1.86.

1.87. Для виробництва промислової продукції створено 3 фірми, кожна з яких випускає один вид продукції. В таблиці задані:

коефіцієнти прямих витрат а_ik, тобто кількість одиниць продукції і -ї фірми, яка використовується як проміжний продукт для випуску одиниці продукції k -ї фірми;

кількість одиниць y_i продукції фірми, розрахованих на реалізацію (кінцевий продукт).

 

Визначити:

а) коефіцієнти повних витрат;

б) валовий випуск (план) для кожної фірми;

в) коефіцієнти непрямих витрат.

Варіант	Фірми	Прямі витрати аik	Кінцевий продукт
І	ІІ	ІІІ	yi
	І	0.1		0.1
	ІІ	0.3		0.1
	ІІІ	0.1	0.2
	І	0.2	0.1
	ІІ		0.3	0.1
	ІІІ	0.2	0.1
	І		0.2	0.2
	ІІ	0.3	0.1
	ІІІ	0.1	0.2	0.1
	І	0.1	0.2
	ІІ	0.2	0.1	0.3
	ІІІ		0.1
	І		0.1	0.3
	ІІ	0.1	0.1
	ІІІ		0.2	0.2
	І	0.2	0.1
	ІІ	0.2		0.1
	ІІІ	0.1	0.1
	І		0.3	0.1
	ІІ	0.3	0.2	0.1
	ІІІ	0.1	0.2
	І	0.2	0.1	0.1
	ІІ	0.2	0.1
	ІІІ	0.1	0.1

 

РОЗДІЛ ІІ. Векторна алгебра

 

Дослідити на лінійну залежність систему векторів.

1.92.

1.93.

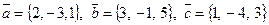
1.94.

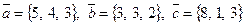
1.95.

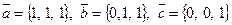
Знайти координати вектора в базисі 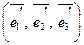, якщо він заданий в базисі .

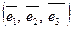1.96.

1.97.

1.98.

Написати розклад вектора по векторам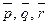

1.99.

1.100.

1.101.

 

Колінеарні вектори і, побудовані на векторах і?

1.117.

1.118.

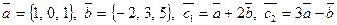
1.119.

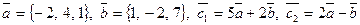
Знайти косинус кута між векторами і.

1.120.

А(1, -2, 3),В(0, -1, 2), С(3, -4, 5)

1.121.

А(0, -3, 6),В(-12, -3, -3), С(-9, -3, -6)

1.122.

А(-1, 2, -3),В(3, 4, -6), С(1, 1, -1)

Обчислити площу паралелограма, побудованого на векторах 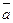і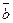

1.123.

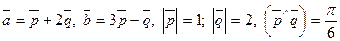
1.124.

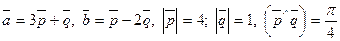
1.125.

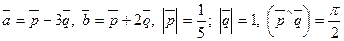
Перевірити на компланарність вектори

1.126.

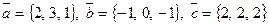
1.127.

1.128.

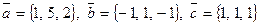
Обчислити об’єм тетраедра з вершинами в точках А₁, А₂, А₃, А₄ та його висоту, опущену із вершини А₄ на грань А₁А₂А₃

1.129. А₁(1, 3, 6), А₂(2, 2, 1), А₃(-1, 0, 1), А₄(-4, 6, -3)

1.130. А₁(-4, 2, 6), А₂(2, -3, 0), А₃(-10, 5, 8), А₄(-5, 2, -4)

1.131. А₁(7, 2, 4), А₂(7, -1, -2), А₃(3, 3, 1), А₄(-4, 2, 1)

 

РОЗДІЛ ІІІ. Аналітична геометрія

1.176 Записати рівняння кола з центром у точці 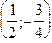і з радіусом, що дорівнює 2. Побудувати це коло.

1.177 Записати рівняння кола, яке проходить через точки А(5;7) і В(-2;4), якщо центр його лежить на прямій 4х+3у-18=0.

1.178 Записати канонічне рівняння еліпса, що проходить через точку М(5;0), якщо фокальна відстань дорівнює 6.

1.179 Довести, що рівняння 36х²+100у²-3600=0 є рівнянням еліпса. Знайти координати фокусів та фокальну відстань.

1.180 Записати рівняння еліпса, фокусами якого є точки 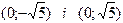, а велика вісь дорівнює 6.

1.181 Записати рівняння еліпса з фокусами на осі ох, якщо відстань між фокусами дорівнює 12, а ексцентриситет Е=0,6.

1.182 Записати рівняння еліпса з фокусами на осі ох, якщо він проходить через точки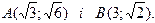

1.183 Побудувати еліпси і . Для кожного еліпса обчислити ексцентриситет.

1.184 Знайти координати точок перетину еліпса 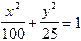з прямою х+2у-14=0.

1.185 Яку лінію визначає рівняння 7х²-9у²=63?

1.186 Знайти напівосі, координати фокусів та ексцентриситет гіперболи, що задані рівнянням 4х²-5у²=20. Обчислити довжини фокальних радіусів точки М(-5;4).

1.187 Записати рівняння асимптот та директрис гіперболи 9х²-25у²=225.

1.188 Гіпербола проходить через точки М 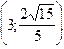та N 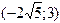. Знайти її канонічне рівняння.

1.189 Написати рівняння дотичних до гіперболи х²-4у²=16, проведених з точки А(0;-2).

1.190 Знайти відстань від фокуса гіперболи 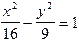до її асимптот та кут між асимптотами.

1.191 Написати рівняння параболи:

1) що проходить через точки (0;0) та (-1;2) і симетрична відносно осі ох;

2) проходить через точки (0;0) та (2;4) і симетрична відносно осі оу.

1.192 Знайти координати фокуса та рівняння директриси параболи у²=20х. Обчислити відстань точки М до фокуса.

1.193 Скласти рівняння параболи, що симетрична відносно осі ох, яка проходить через точки М(4;-5) та N (6;15).

1.194 На параболі у²=6х знайти точку М, фокальний радіус якої дорівнює 4,5.

1.195 Написати рівняння дотичних до параболи у²=8х, проведених з точки А(0;-2).

1.196 Скласти параметричне рівняння кола, якщо точка М(х;у) описує коло радіуса r з центром на початку координат.

1.197 Дано рівняння еліпса 9х²+16у²=144. Записати його параметричне рівняння.

1.198 Дано параметричні рівняння еліпса х=5cost, y=3sint, t Î[0;2p). Записати його канонічне рівняння.

1.205 Знайти координати центра і радіус сфери, заданої рівнянням

x ²+ y ²+ z ²- x +2 y +1=0

1.206 Скласти рівняння сфери, яка проходить через точки А (1;2;-4), В (1;-3;1) і С (2;2;3), якщо центр знаходиться в площині хоу.

 

1.207 По якій лінії перетинається конус x ²+ y ²-2 z ²=0 з площиною у =2?

1.208 Привести до канонічного вигляду рівняння x ²- y ²-4 x +8 y -2 z =0.

1.209 Яка поверхня визначається рівнянням 4 x ²- y ²+4 z ²-8 x +4 y +8 z +4=0?

 

1.210 Який геометричний зміст рівняння х ²+ y ²+ z ²- yz - xz - ху =0?

 

1.142. Визначити площу S та периметр трикутника, утвореного прямою 3 х -4 у -12=0 і осями координат.

1.143. Записати рівняння прямої, що проходить через початок координат і точку (-1;8).

1.144. Дано вершини трикутника А(1;-2), В(5;4) і С(-2; 0). Записати рівняння бісектриси його внутрішнього кута при вершині А.

1.145. Записати рівняння прямих, на яких лежать катети рівнобічного прямокутного трикутника, знаючи рівняння прямої, на якій лежить гіпотенуза 3 х - у+ 5=0 і вершину кута С (4;-1).

х -2 у -6=0 і 2 х+у -7=0.

1.146. Встановити, які з пар прямих паралельні, співпадають або перетинаються, в останньому випадку знайти їх точку перетину:

1) х + у -3=0 і 2 х +3 у -8=0

2) у = х +5 і 2 х -2 у +3=0

3) у= 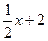і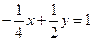

1.147. Визначити точку, симетричну з точкою М (8;-9) відносно прямої, яка проходить через точки А (3;-4) і В (-1;-2).

1.148. Записати рівняння прямих, на яких лежать катети рівнобічного прямокутного трикутника, знаючи рівняння прямої на якій лежить гіпотенуза 3 х - у+ 5=0 і вершину прямого кута С (4;-1).

Обчислити величину кута між прямими:

1) у =3 х і у =-2 х +5;

2) у =4 х- 7 і у = +2;

3) у =5 х -3 і у =5 х +8.

1.149. Основа рівнобедреного трикутника лежить на прямій х- 2 у =0, а одна з бічних сторін на прямій х+у -3=0. Записати рівняння прямої, на якій лежить друга бічна сторона, знаючи, що вона проходить через точку (1;-1).

1.150. Записати рівняння прямої, паралельної і рівновіддаленої від двох паралельних прямих х+у -1=0 і х+у+ 13=0.

1.151. Записати рівняння прямої, на якій лежить перпендикуляр, встановлений у точці перетину прямих 4 х+ 3 у -5=0 і 8 х- 5 у +23=0, до першої прямої.

1.152. Записати рівняння прямої, на якій лежать бісектриси кутів між прямими

3 х- 4 у+ 7=0 і 5 х+ 12 у -1=0.

1.153. При яких значеннях параметра “ а ” пряма (а +2) х +(а ²+9) у +3 а ²-8 а +5=0:

1) паралельна осі Ох;

2) паралельна осі Оу;

3) проходить через початок координат?

1.154. Записати рівняння прямих, на яких розміщені сторони трикутника АВС, знаючи координати вершини А (1;3) та рівняння двох його медіан у -1=0 і х- 2 у+ 1=0.

1.155. Записати рівняння сторін трикутника АВС, якщо задано координати однієї із його вершин В(-4;-5) і рівняння прямих, на яких лежать дві його висоти: 5 х+ 3 у -4=0 і 3 х+ 8 у+ 13=0.

1.156. Дві сторони квадрата лежать на прямих 5 х- 12 у -65=0, 5 х- 12 у +26=0.

Обчислити площу квадрата.

1.157. Знайти рівняння площини, яка проходить через точку М (2; 3; -1) паралельно площині 5 х -3 у +2 z -10=0.

1.158. Знайти довжину перпендикуляра, який опущений із точки М₀ (2; 3; -5) на площину 4 х -2 у +5 z -12=0.

1.159. Знайти рівняння площини, яка проходить через точку Р(2; 0; -1) і Q(1; -1; 3) перпендикулярно площині 3 х +2 у-z+ 5=0.

1.160. Знайти рівняння площини, яка проходить через початок координат і через точки Р (4; -2; 1) і Q (2; 4; -3).

1.161. Знайти рівняння площини, яка проходить через лінію перетину площин х +5 у+ 9 z+ 13=0, 3 х - у- 5 z+ 1=0 і через точку М (0; 2; 1).

1.162. Скласти рівняння площини, яка проходить через лінію перетину площин 2х-у-12 z- 3=0 і 3 х + у- 7 z- 2=0 і перпендикулярно площині х +2 у+ 5 z -1=0.

1.163. Скласти рівняння площини, яка проходить через точку М (0; 2; 1) і паралельно векторам і .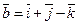

1.164. Знайти рівняння прямої, яка проходить через точку N (5; -1; -3) і паралельно прямій

1.165. Обчислити відстань між паралельними прямими ; .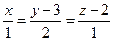

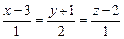1.166. Задані точки А (-1; 2; 3) і В (2; -3; 1). Скласти рівняння прямої, яка проходить через точку М (3; -1; 2) і паралельна вектору .

1.167. Знайти кут між прямими

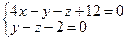і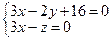

1.168. Задані точки А (1; 1; 1), В (2; 3; 3) і С (3; 3; 2). Скласти рівняння прямої, яка проходить через точку А і перпендикулярно вектором і .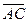

1.169. Знайти рівняння площини, яка проходить через пряму 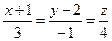і перпендикулярно площині: 3 х + у-z+ 2=0.

1.170. Знайти рівняння проекції прямої на площину 2 х +3 у-z- 5=0.