Лекция 12
Уравнения прямой в 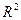
Если в 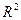 задана точка
задана точка 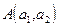 и ненулевой вектор
и ненулевой вектор 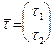 , то точно так же, как мы ранее получили параметрические уравнения (42) прямой в
, то точно так же, как мы ранее получили параметрические уравнения (42) прямой в  , можно записать следующие параметрические уравнения прямой в
, можно записать следующие параметрические уравнения прямой в 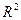 :
:
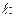 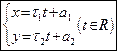 . .
| (46) |
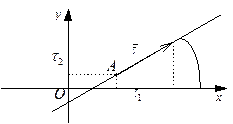
|
Определение 28. Если 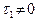 (то есть если прямая
(то есть если прямая  непараллельна оси Oy), то число
непараллельна оси Oy), то число 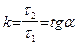 (где
(где 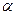 – угол наклона прямой
– угол наклона прямой  к оси Ox) называется угловым коэффициентом прямой
к оси Ox) называется угловым коэффициентом прямой  . В случае
. В случае 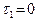 (то есть если прямая
(то есть если прямая  параллельна оси Oy) говорят, что прямая
параллельна оси Oy) говорят, что прямая  имеет бесконечный угловой коэффициент.
имеет бесконечный угловой коэффициент.
Преобразуем уравнения (46) в обоих случаях, указанных в определении 28.
1) Пусть 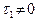 . Выразим параметр t из первого уравнения в (46) и подставим во второе уравнение. Получим:
. Выразим параметр t из первого уравнения в (46) и подставим во второе уравнение. Получим:
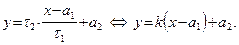
|
Уравнение
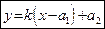
| (47) |
называется уравнением прямой в 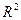 , проходящей через точку
, проходящей через точку 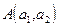 с угловым коэффициентом k. Раскрывая в (47) скобки и обозначая
с угловым коэффициентом k. Раскрывая в (47) скобки и обозначая 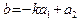 , получаем уравнение
, получаем уравнение
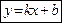 , ,
| (48) |
называемое уравнением прямой в 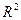 с угловым коэффициентом k. Если в уравнении (48) положить
с угловым коэффициентом k. Если в уравнении (48) положить 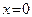 , то получим
, то получим 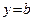 , то есть число b есть ордината точки пересечения прямой
, то есть число b есть ордината точки пересечения прямой  и оси Oy.
и оси Oy.
2) Если 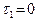 , то
, то 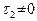 . Отсюда немедленно следует, что система (46) равносильна уравнению
. Отсюда немедленно следует, что система (46) равносильна уравнению 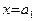 . Итак, уравнение вида
. Итак, уравнение вида
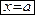
| (49) |
есть уравнение прямой в 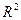 , параллельной оси Oy.
, параллельной оси Oy.
Пример 27. Записать уравнение прямой, проходящей через точку 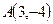 и наклоненной к оси Ox под углом
и наклоненной к оси Ox под углом 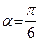 .
.
Подставим в уравнение (47) 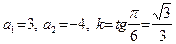 . Уравнение искомой прямой запишется в виде:
. Уравнение искомой прямой запишется в виде: 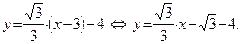
Пример 28. Записать уравнение прямой, проходящей через точку 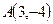 и параллельной оси Oy.
и параллельной оси Oy.
Применяя (49), имеем: 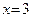 .
.
Используя (46), получим теперь уравнение прямой, проходящей через две точки 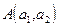 и
и 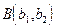 . Очевидно, можно положить
. Очевидно, можно положить 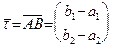 . Тогда уравнения (46) примут вид:
. Тогда уравнения (46) примут вид:
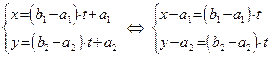 . .
|
Применяя свойство 6 определителей, получаем:
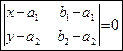 . .
| (50) |
Обратно, если (50) выполняется, то по свойству 5 систем векторов векторы-столбцы в определителе (50) линейно зависимы. А так как второй вектор-столбец – ненулевой, то легко видеть, что первый вектор-столбец равен второму, умноженному на некоторое число t.
Итак, мы доказали, что уравнение (50) есть уравнение прямой в 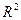 , проходящей через две заданные точки A и B.
, проходящей через две заданные точки A и B.
Общее уравнение прямой в 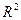 . Угол между двумя прямыми.
. Угол между двумя прямыми.
Условие ортогональности двух прямых. Построение прямых в 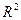 и плоскостей в
и плоскостей в  .
.
Определение 29. Уравнение 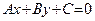 , где A, B и C – действительные числа, причем хотя бы одно из чисел A и B неравно нулю, называется общим уравнением прямой в
, где A, B и C – действительные числа, причем хотя бы одно из чисел A и B неравно нулю, называется общим уравнением прямой в 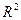 .
.
Точно так же, как это делалось в доказательстве теоремы 19, можно доказать следующий результат:
Теорема 21. Общее уравнение прямой сводится к одному из уравнений (48) или (49), причем вектор 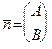 является нормальным вектором данной прямой
является нормальным вектором данной прямой 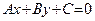 .
.
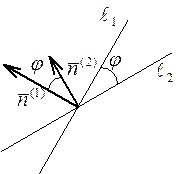
|
Пусть даны две прямые 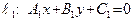 и
и 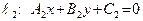 . Очевидно, угол
. Очевидно, угол 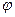 между их нормальными векторами
между их нормальными векторами 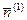 и
и 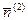 равен одному из углов, образованных самими прямыми
равен одному из углов, образованных самими прямыми  и
и 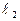 (на рисунке этот угол является острым; однако если бы вектора
(на рисунке этот угол является острым; однако если бы вектора 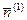 и
и 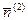 смотрели в разные стороны, то этот угол оказался бы тупым). По формуле (25) и с учетом теоремы 21 имеем:
смотрели в разные стороны, то этот угол оказался бы тупым). По формуле (25) и с учетом теоремы 21 имеем:
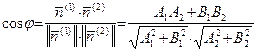 . .
| (51) |
Итак, по формуле (51) можно вычислять один из углов, образованных прямыми  и
и 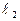 .
.
Из (51) вытекает, что  перпендикулярна
перпендикулярна 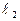 тогда и только тогда, когда
тогда и только тогда, когда 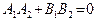 . Преобразуем это соотношение. Сначала предположим, что
. Преобразуем это соотношение. Сначала предположим, что 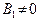 и
и 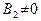 . Это означает, что угловые коэффициенты прямых
. Это означает, что угловые коэффициенты прямых  и
и 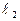 конечны. Имеем:
конечны. Имеем:
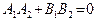
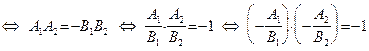 .
.
Однако из уравнений  и
и 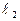 легко получить, что выражения в скобках соответственно равны угловым коэффициентам этих прямых:
легко получить, что выражения в скобках соответственно равны угловым коэффициентам этих прямых: 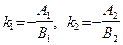 . Таким образом, имеем:
. Таким образом, имеем:
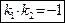 . .
| (52) |
Заметим, что соотношение (52) можно применять и в случае, когда одна из прямых  и
и 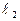 имеет бесконечный угловой коэффициент. Пусть, например,
имеет бесконечный угловой коэффициент. Пусть, например, 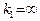 . Если при этом положить
. Если при этом положить 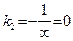 , то прямые
, то прямые  и
и 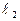 будут перпендикулярны, так как
будут перпендикулярны, так как 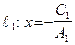 параллельна оси Oy, а
параллельна оси Oy, а 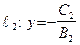 параллельна оси Ox.
параллельна оси Ox.
Итак, мы получили, что две прямые  и
и 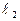 ортогональны тогда и только тогда, когда выполняется равенство (52), то есть произведение угловых коэффициентов этих прямых равно минус единице.
ортогональны тогда и только тогда, когда выполняется равенство (52), то есть произведение угловых коэффициентов этих прямых равно минус единице.
Пример 29. Даны вершины треугольника 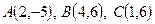 . Найти уравнения сторон AB и BC и уравнения высот треугольника, опущенных на эти стороны.
. Найти уравнения сторон AB и BC и уравнения высот треугольника, опущенных на эти стороны.
Для нахождения уравнений AB и BC применим формулу (50):
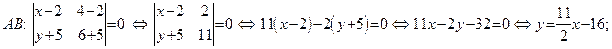
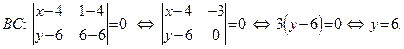
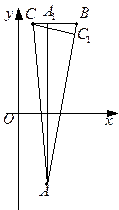
|
Из полученных уравнений находим угловые коэффициенты прямых AB и BC: 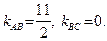 Пользуясь условием ортогональности (52), найдем угловые коэффициенты
Пользуясь условием ортогональности (52), найдем угловые коэффициенты 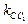 и
и 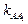 высот
высот 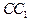 и
и 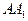 :
: 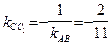 ,
, 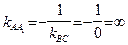 . Используя формулу (47), запишем уравнение высоты
. Используя формулу (47), запишем уравнение высоты 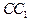 , проходящей через известную точку
, проходящей через известную точку 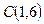 и имеющей известный угловой коэффициент
и имеющей известный угловой коэффициент 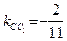 :
:
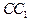 :
: 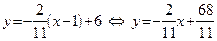 .
.
Ввиду того, что угловой коэффициент высоты 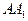 бесконечен, эта высота, согласно (49), имеет уравнение вида
бесконечен, эта высота, согласно (49), имеет уравнение вида 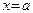 . Так как она проходит через точку
. Так как она проходит через точку 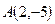 , то ясно, что
, то ясно, что 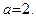 Таким образом,
Таким образом, 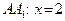 .
.
Пример 30. Построить прямые:
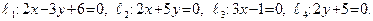
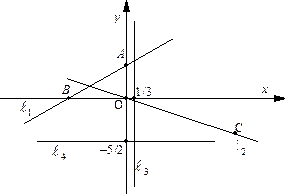
|
Для построения прямой  применим так называемый метод в отрезках на осях. Полагая в уравнении
применим так называемый метод в отрезках на осях. Полагая в уравнении 
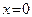 , получаем
, получаем 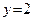 , то есть находим точку
, то есть находим точку 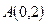 пересечения
пересечения  и оси Oy. Полагая
и оси Oy. Полагая 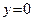 , получаем
, получаем 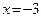 , то есть находим точку
, то есть находим точку 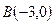 пересечения
пересечения  и оси Ox. Теперь проводим прямую
и оси Ox. Теперь проводим прямую  через точки A и B.
через точки A и B.
Очевидно, что прямая 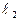 проходит через начало координат
проходит через начало координат 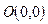 . Вторую точку на
. Вторую точку на 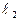 находим, придавая переменной x какое-либо ненулевое значение. Пусть
находим, придавая переменной x какое-либо ненулевое значение. Пусть 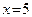 , тогда
, тогда 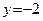 , и мы получаем точку
, и мы получаем точку 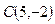 на
на 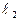 . Осталось соединить точки O и C.
. Осталось соединить точки O и C.
Преобразуем уравнение прямой 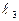 к виду (49):
к виду (49): 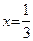 . Это прямая, параллельная оси Oy и пересекающая ось Ox в точке
. Это прямая, параллельная оси Oy и пересекающая ось Ox в точке 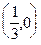 .
.
Преобразуем уравнение прямой 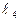 к виду:
к виду: 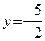 . Это прямая, параллельная оси Ox и пересекающая ось Oy в точке
. Это прямая, параллельная оси Ox и пересекающая ось Oy в точке 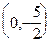 .
.
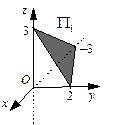
|
Пример 31. Построить в  следующие плоскости:
следующие плоскости: 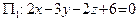 ,
, 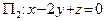 ,
, 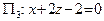 ,
, 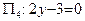 .
.
Построим 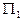 в отрезках на осях (см. пример 30). Имеем:
в отрезках на осях (см. пример 30). Имеем:
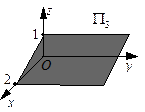
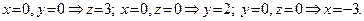 Построив три вычисленные точки и соединив их отрезками, получаем треугольник, лежащий в искомой плоскости
Построив три вычисленные точки и соединив их отрезками, получаем треугольник, лежащий в искомой плоскости 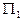 .
.
|
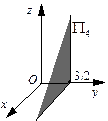
|
Построим плоскость 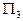 . Уравнение
. Уравнение 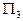 не содержит переменной y. Это означает, что если точка
не содержит переменной y. Это означает, что если точка 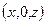 принадлежит
принадлежит 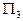 , то этой плоскости принадлежит и точка
, то этой плоскости принадлежит и точка 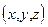 при любом
при любом 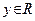 . Итак, вместе с точкой
. Итак, вместе с точкой 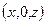 плоскости
плоскости 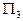 принадлежит вся прямая, проходящая через эту точку и параллельная оси Oy. Из уравнения
принадлежит вся прямая, проходящая через эту точку и параллельная оси Oy. Из уравнения 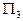 получаем:
получаем: 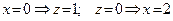 . Соединив точки
. Соединив точки 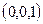 и
и 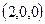 и проведя через каждую из этих точек прямую, параллельную оси Oy, получим нужную плоскость.
и проведя через каждую из этих точек прямую, параллельную оси Oy, получим нужную плоскость.
Уравнение плоскости 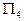 запишем в виде:
запишем в виде: 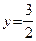 . Очевидно, это плоскость, проходящая через точку
. Очевидно, это плоскость, проходящая через точку 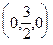 параллельно координатной плоскости xOz.
параллельно координатной плоскости xOz.
Построение плоскости 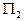 немного сложнее и предоставляется читателю.
немного сложнее и предоставляется читателю.






