ЛИНЕЙНАЯ АЛГЕБРА
И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Раздел 2. Линейная алгебра
Курс лекций
и образец решения индивидуального задания
по высшей математике для бакалавров 1-го курса
очной формы обучения
Ростов-на-Дону
УДК 517(07)
Линейная алгебра и аналитическая геометрия. Раздел 2. Линейная алгебра. Курс лекций и образец решения индивидуального задания по высшей математике для бакалавров 1-го курса очной формы обучения. – Ростов н/Д: Рост. гос. строит. ун-т, 2011. – 33 с.
Изложен курс лекций по линейным образам (уравнения прямых и плоскостей). Приведен образец индивидуального задания, снабженный подробным решением входящих в него задач.
Предназначены для бакалавров 1-го курса очной формы, проходящих обучение на кафедре высшей математики РГСУ, а также на математических кафедрах других вузов.
Электронная версия находится в библиотеке, ауд. 224.
УДК 517(07)
| Составитель: | д-р физ.-мат. наук, проф. И.В. Павлов |
| Рецензенты: | канд. физ.-мат. наук, доц. А.М. Можаев, канд. физ.-мат. наук, доц. Г.А. Власков |
Редактор Т.М. Климчук
Доп. план 2011 г., поз. 177
Подписано в печать 12.07.11. Формат 60´84/16. Бумага писчая. Ризограф.
Уч.-изд.л. 2,5. Тираж 50 экз. Заказ 379
Редакционно-издательский центр
Ростовского государственного строительного университета
344022, Ростов-на-Дону, ул. Социалистическая, 162
© Ростовский государственный
строительный университет, 2011
ЧАСТЬ 3: УРАВНЕНИЯ ПРЯМЫХ И ПЛОСКОСТЕЙ
Лекция 10
Параметрические уравнения прямой в 
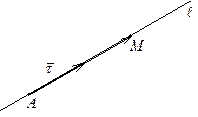
|
Дано: точка 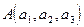 и ненулевой вектор
и ненулевой вектор 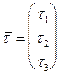 .
.
Требуется: записать уравнение прямой  , проходящей через точку A и вектор
, проходящей через точку A и вектор  (предполагается, что начало вектора
(предполагается, что начало вектора  совмещено с точкой A).
совмещено с точкой A).
Решение. Рассмотрим на прямой  так называемую "текущую" точку
так называемую "текущую" точку  с переменными координатами x, y и z. Наложим на переменные x, y и z такие условия, которые, с одной стороны, дадут возможность точке M попасть в любую точку прямой
с переменными координатами x, y и z. Наложим на переменные x, y и z такие условия, которые, с одной стороны, дадут возможность точке M попасть в любую точку прямой  и, с другой стороны, не позволят точке M выйти за пределы прямой
и, с другой стороны, не позволят точке M выйти за пределы прямой  . Полученные соотношения и будут представлять собой уравнения прямой
. Полученные соотношения и будут представлять собой уравнения прямой  . Имеем цепочку равносильностей (в этой цепочке символ
. Имеем цепочку равносильностей (в этой цепочке символ 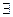 будет заменять слово "существует"):
будет заменять слово "существует"):
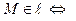 вектора
вектора  и
и 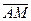 линейно зависимы
линейно зависимы 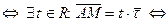
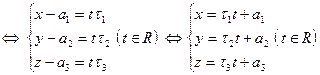 .
.
Система уравнений
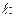 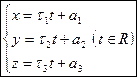
| (42) |
называется параметрическими уравнениями прямой в  по точке А и вектору
по точке А и вектору  . Число t является в уравнениях (42) параметром, могущим принимать любое действительное значение. Вектор
. Число t является в уравнениях (42) параметром, могущим принимать любое действительное значение. Вектор  (как и любой вектор, параллельный прямой
(как и любой вектор, параллельный прямой  ) называют направляющим вектором прямой
) называют направляющим вектором прямой  .
.
Числовая иллюстрация. Запишем уравнения прямой  , проходящей через точку
, проходящей через точку  и вектор
и вектор  . Подставив имеющиеся данные в уравнение (42), получим:
. Подставив имеющиеся данные в уравнение (42), получим:
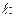  . .
| (43) |
Применяя уравнения (42) к решению конкретных задач, следует, прежде всего, отдавать себе отчет в двух вещах.
1) Чтобы получать точки прямой  , нужно придавать параметру t различные действительные значения. Например, если требуется найти какие-либо три различные точки на прямой (43), то можно сначала выбрать самое простое значение параметра, а именно
, нужно придавать параметру t различные действительные значения. Например, если требуется найти какие-либо три различные точки на прямой (43), то можно сначала выбрать самое простое значение параметра, а именно 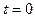 , и, подставив в (43), получить исходную точку A. Затем выбираем какие-нибудь еще два значения параметра, к примеру,
, и, подставив в (43), получить исходную точку A. Затем выбираем какие-нибудь еще два значения параметра, к примеру, 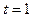 и
и  , и получаем, соответственно, точки
, и получаем, соответственно, точки  и
и  , лежащие на прямой
, лежащие на прямой  . Если существует произвол в выборе точек, то ясно, что третье значение параметра брать не стоит.
. Если существует произвол в выборе точек, то ясно, что третье значение параметра брать не стоит.
2) Если нужно проверить, лежат ли, например, точки 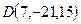 и
и  на прямой (43), в каждом случае следует подставлять координаты данных точек вместо x, y и z в уравнение (43) и решать полученную систему 3-х уравнений с одним неизвестным. Если система окажется совместной, то точка лежит на прямой, а если несовместной – то не лежит.
на прямой (43), в каждом случае следует подставлять координаты данных точек вместо x, y и z в уравнение (43) и решать полученную систему 3-х уравнений с одним неизвестным. Если система окажется совместной, то точка лежит на прямой, а если несовместной – то не лежит.
Имеем для точки D:
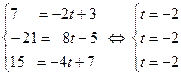 . .
|
Система совместна,  и точке D соответствует значение параметра
и точке D соответствует значение параметра 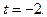
Для точки E:
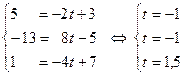 . .
|
Система несовместна, следовательно 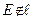 .
.
Пример 21. Записать уравнения прямой, проходящей через точки  и
и 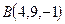 .
.

|
Ясно, что направляющий вектор для  можно задать так:
можно задать так:
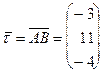
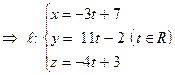 .
.
Пример 22. Записать уравнение прямой, проходящей через точку 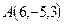 перпендикулярно векторам
перпендикулярно векторам  и
и 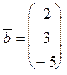 .
.

|
Принимая во внимание теорему 15, направляющий вектор для  можно вычислить следующим образом:
можно вычислить следующим образом:
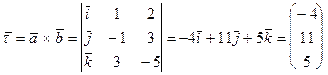 .
.
Следовательно, 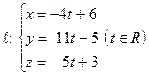 .
.
Уравнение плоскости по точке и нормальному вектору

|
Дано: точка 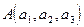 и ненулевой вектор
и ненулевой вектор  .
.
Требуется: записать уравнение плоскости 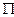 , проходящей через точку A ортогонально вектору
, проходящей через точку A ортогонально вектору 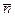 .
.
Решение. Рассмотрим на плоскости 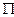 "текущую" точку
"текущую" точку  с переменными координатами x, y и z. Наложим на переменные x, y и z условие, которое, с одной стороны, даст возможность точке M попасть в любую точку плоскости
с переменными координатами x, y и z. Наложим на переменные x, y и z условие, которое, с одной стороны, даст возможность точке M попасть в любую точку плоскости 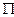 и, с другой стороны, не позволит точке M выйти за пределы этой плоскости. Полученное соотношение и будет представлять собой уравнения плоскости
и, с другой стороны, не позволит точке M выйти за пределы этой плоскости. Полученное соотношение и будет представлять собой уравнения плоскости 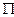 . Имеем цепочку равносильностей:
. Имеем цепочку равносильностей:
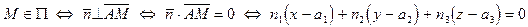 .
.
Уравнение
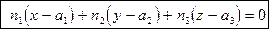
| (44) |
называется уравнением плоскости по точке A и нормальному вектору 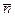 (термины "нормальный вектор", "ортогональный вектор", "перпендикулярный вектор" означают одно и то же).
(термины "нормальный вектор", "ортогональный вектор", "перпендикулярный вектор" означают одно и то же).
Числовая иллюстрация. Запишем уравнение плоскости, проходящей через точку 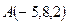 и имеющей нормальный вектор
и имеющей нормальный вектор 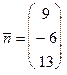 . По формуле (44) имеем:
. По формуле (44) имеем:
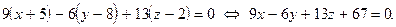
Уравнение плоскости по точке и двум векторам
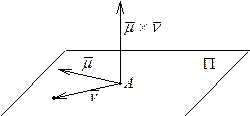
|
Дано: точка 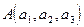 и два линейно независимых (неколлинеарных) вектора
и два линейно независимых (неколлинеарных) вектора 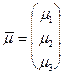 и
и 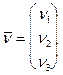 .
.
Требуется: записать уравнение плоскости, проходящей через точку A и векторы 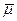 и
и  (предполагается, что начала векторов
(предполагается, что начала векторов 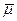 и
и  совмещены с точкой A).
совмещены с точкой A).
Решение. Сведем эту задачу к задаче построения уравнения плоскости по точке и нормальному вектору. Очевидно, в качестве нормального вектора можно выбрать вектор 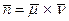 . Взяв текущую точку
. Взяв текущую точку 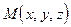 и применяя рассуждения предыдущего пункта, а также определение 26 и теорему 16, получаем:
и применяя рассуждения предыдущего пункта, а также определение 26 и теорему 16, получаем:
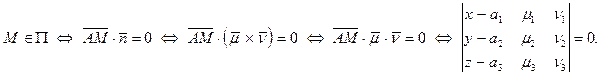
Уравнение

| (45) |
называется уравнением плоскости по точке A и двум векторам 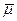 и
и  .
.
Пример 23. Доказать, что прямые 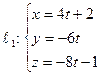 и
и 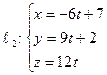 параллельны, но не совпадают, и записать уравнение плоскости, проходящей через
параллельны, но не совпадают, и записать уравнение плоскости, проходящей через  и
и 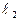 .
.
1) Направляющие векторы данных прямых соответственно равны 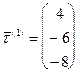 и
и  . Так как отношения соответствующих координат равны
. Так как отношения соответствующих координат равны 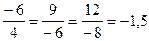 , то
, то  , то есть эти векторы линейно зависимы (коллинеарны). Значит,
, то есть эти векторы линейно зависимы (коллинеарны). Значит, 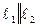 .
.
2) Теперь чтобы доказать, что  и
и 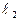 не совпадают, достаточно проверить, что точка, лежащая на одной прямой, не лежит на другой. Положив
не совпадают, достаточно проверить, что точка, лежащая на одной прямой, не лежит на другой. Положив 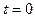 в первой системе, получаем точку
в первой системе, получаем точку 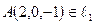 . Покажем, что
. Покажем, что  . Подставим координаты точки A во вторую систему:
. Подставим координаты точки A во вторую систему: 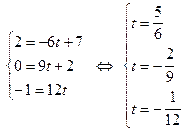 . Эта система противоречива, поэтому
. Эта система противоречива, поэтому  .
.

|
3) Запишем уравнение плоскости, проходящей через  и
и 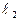 . Положив
. Положив 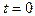 в параметрических уравнениях прямой
в параметрических уравнениях прямой 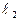 , получим точку
, получим точку 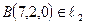 . Возьмем
. Возьмем 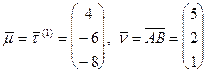 . По формуле (45) получаем искомое уравнение плоскости:
. По формуле (45) получаем искомое уравнение плоскости:

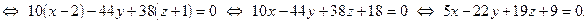
ЧАСТЬ 3: УРАВНЕНИЯ ПРЯМЫХ И ПЛОСКОСТЕЙ
Лекция 11
Пример 24. Доказать, что прямые 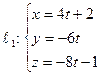 и
и 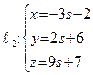 пересекаются, и записать уравнение плоскости, проходящей через
пересекаются, и записать уравнение плоскости, проходящей через  и
и 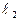 .
.
Прежде всего отметим, что при записи уравнений данных прямых мы обозначили параметры разными буквами. В принципе, это нужно делать всегда для двух различных прямых. Этим правилом пренебрегают, когда в процессе решения эти параметры не входят одновременно в состав какого-либо одного уравнения (см. пример 23). Как мы увидим, при решении данного примера без четкого различения параметров не обойтись.
1) Покажем, что  и
и 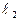 пересекаются. Это означает, что должна существовать единственная точка
пересекаются. Это означает, что должна существовать единственная точка 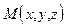 , координаты которой удовлетворяют одновременно всем уравнениям первой и второй прямой. А это выполняется тогда и только тогда, когда следующая система имеет единственное решение:
, координаты которой удовлетворяют одновременно всем уравнениям первой и второй прямой. А это выполняется тогда и только тогда, когда следующая система имеет единственное решение:



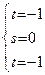 .
.
Единственное решение получено и, подставляя  в уравнения прямой
в уравнения прямой  (либо
(либо 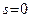 в уравнения прямой
в уравнения прямой 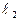 ), получаем точку пересечения
), получаем точку пересечения  .
.
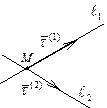
|
2) Прямые  и
и 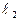 пересекаются в точке
пересекаются в точке  и имеют направляющие векторы
и имеют направляющие векторы 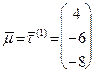 и
и 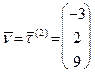 . Записывая уравнение плоскости по точке и двум векторам (см. формулу (45)), получаем:
. Записывая уравнение плоскости по точке и двум векторам (см. формулу (45)), получаем:
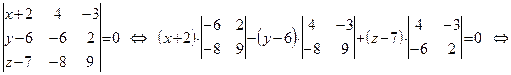

Общее уравнение плоскости в 
Определение 27. Уравнение 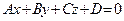 , где A, B, C и D – действительные числа, причем A, B и C не равны нулю одновременно, называется общим уравнением плоскости в пространстве
, где A, B, C и D – действительные числа, причем A, B и C не равны нулю одновременно, называется общим уравнением плоскости в пространстве  .
.
Легко видеть, что изученные ранее уравнения плоскости (44) и (45) после преобразований сводятся к общему уравнению плоскости (это также наглядно видно в примерах 23 и 24).
Теорема 19. Вектор  является нормальным вектором плоскости
является нормальным вектором плоскости 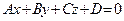 .
.
Доказательство. Пусть  – точка, лежащая на заданной плоскости, то есть
– точка, лежащая на заданной плоскости, то есть 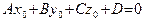 . Такая точка всегда существует. Например, если
. Такая точка всегда существует. Например, если  , то можно положить
, то можно положить  (случаи
(случаи  и
и 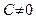 рассматриваются аналогично). Пользуясь формулой (44), запишем уравнение плоскости
рассматриваются аналогично). Пользуясь формулой (44), запишем уравнение плоскости  , проходящей через точку
, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору 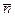 :
:
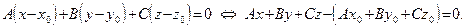
Так как 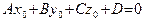 , то
, то 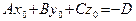 и уравнение плоскости
и уравнение плоскости  принимает вид
принимает вид 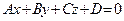 , то есть исходная плоскость совпадает с плоскостью
, то есть исходная плоскость совпадает с плоскостью  . Значит нормальный вектор плоскости
. Значит нормальный вектор плоскости  также является нормальным вектором исходной плоскости.
также является нормальным вектором исходной плоскости.
Заметим, что из доказательства теоремы 19 следует более сильный вывод: плоскость, заданная общим уравнением, всегда может быть получена с помощью формулы (44).
Теорема 20. Пусть даны плоскость  :
: 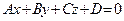 и прямая
и прямая 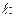
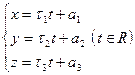 .
.
1) 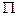 и
и  пересекаются тогда и только тогда, когда
пересекаются тогда и только тогда, когда 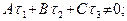
2)  лежит в плоскости
лежит в плоскости  тогда и только тогда, когда
тогда и только тогда, когда 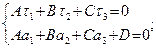
3)  параллельна
параллельна  (но не лежит в плоскости
(но не лежит в плоскости  ) тогда и только тогда, когда
) тогда и только тогда, когда 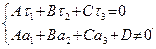
Доказательство. Для нахождения общих точек плоскости  и прямой
и прямой  составляем систему уравнений:
составляем систему уравнений:

Преобразовывая последнее уравнение полученной системы, имеем:
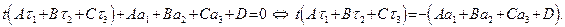
Если 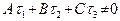 , то
, то 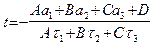 и, подставляя это значение t в первые три уравнения системы, находим однозначно определенные координаты x, y и z точки пересечения
и, подставляя это значение t в первые три уравнения системы, находим однозначно определенные координаты x, y и z точки пересечения  и
и  . Если
. Если 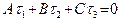 и
и 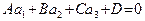 , то получаем верное равенство
, то получаем верное равенство 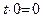 , которое означает, что каждая точка прямой
, которое означает, что каждая точка прямой  лежит в плоскости
лежит в плоскости  . Наконец, если
. Наконец, если 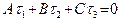 , но
, но  , то левая часть полученного уравнения равна нулю, а правая отлична от нуля. Это говорит о том, что исходная система несовместна, следовательно
, то левая часть полученного уравнения равна нулю, а правая отлична от нуля. Это говорит о том, что исходная система несовместна, следовательно  и
и  не имеют общих точек, то есть
не имеют общих точек, то есть 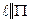 .
.
Геометрический смысл теоремы 20 очень прост. Так как 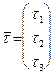 – направляющий вектор прямой
– направляющий вектор прямой  , а
, а  – нормальный вектор плоскости
– нормальный вектор плоскости  , то условие пункта 1) теоремы 20 означает, что
, то условие пункта 1) теоремы 20 означает, что  , то есть угол между
, то есть угол между 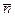 и
и  неравен
неравен 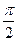 . А это и означает, что
. А это и означает, что  непараллельна
непараллельна  . Наоборот, в пунктах 2) и 3)
. Наоборот, в пунктах 2) и 3) 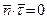 , то есть
, то есть  параллельна
параллельна  в широком смысле. Если при этом
в широком смысле. Если при этом 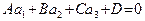 (то есть точка
(то есть точка  , принадлежащая прямой
, принадлежащая прямой  , принадлежит также и
, принадлежит также и  ), то ясно, что тогда и все точки
), то ясно, что тогда и все точки  принадлежат
принадлежат  . В противном случае
. В противном случае  и
и  не имеют общих точек, то есть
не имеют общих точек, то есть 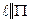 .
.
Пример 25. Найти точку Q, симметричную точке 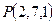 относительно плоскости
относительно плоскости 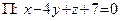 .
.

|
1) Запишем уравнение прямой  , проходящей через точку P перпендикулярно плоскости
, проходящей через точку P перпендикулярно плоскости  . Так как в качестве направляющего вектора
. Так как в качестве направляющего вектора  прямой
прямой  можно взять нормальный вектор плоскости
можно взять нормальный вектор плоскости  , который в силу теоремы 19 равен
, который в силу теоремы 19 равен 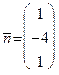 , то параметрические уравнения
, то параметрические уравнения  имеют вид:
имеют вид: 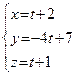 .
.
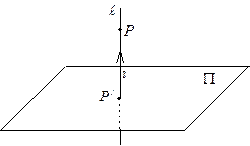
|
2) Найдем точку пересечения  прямой
прямой  и плоскости
и плоскости  . Так же, как и в доказательстве теоремы 20, решим систему уравнений:
. Так же, как и в доказательстве теоремы 20, решим систему уравнений:
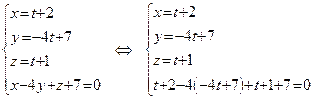 .
.
Таким образом,  То есть,
То есть,  .
.
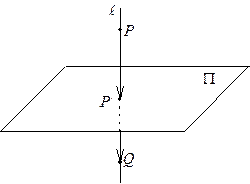
|
3) Пусть 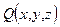 – точка, симметричная точке P относительно плоскости
– точка, симметричная точке P относительно плоскости  . Так как
. Так как 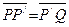 , то
, то 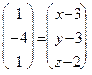
 . То есть
. То есть  .
.

|
Пример 26. Найти точку Q, симметричную точке  относительно прямой
относительно прямой  :
: 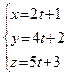 .
.
1) Запишем уравнение плоскости  , проходящей через точку P перпендикулярно прямой
, проходящей через точку P перпендикулярно прямой  . Так как в качестве нормального вектора плоскости
. Так как в качестве нормального вектора плоскости  можно взять направляющий вектор прямой
можно взять направляющий вектор прямой  , который равен
, который равен 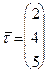 , то по формуле (44):
, то по формуле (44): 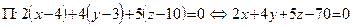 .
.

|
2) Найдем точку пересечения  прямой
прямой  и плоскости
и плоскости  . Решим систему уравнений:
. Решим систему уравнений:

Получаем:  То есть
То есть 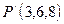 .
.

|
3) Пусть 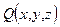 – точка, симметричная точке P относительно прямой
– точка, симметричная точке P относительно прямой  . Так как
. Так как 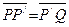 , то
, то 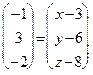
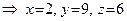 . То есть
. То есть 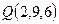 .
.
Прямая как линия пересечения двух плоскостей
Пусть заданы две плоскости:  и
и 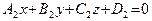 , причем их нормальные векторы
, причем их нормальные векторы 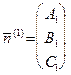 и
и 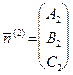 неколлинеарны. Отсюда следует, что эти плоскости пересекаются, то есть система
неколлинеарны. Отсюда следует, что эти плоскости пересекаются, то есть система 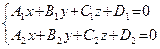 определяет прямую в пространстве
определяет прямую в пространстве  . Читателю предлагается самостоятельно разобраться, как из этой системы получить параметрические уравнения данной прямой.
. Читателю предлагается самостоятельно разобраться, как из этой системы получить параметрические уравнения данной прямой.






