Вопросы
1. Понятие объема фигуры (определение, свойства).
2. Объем прямого цилиндра (формулировка, доказательство).
3. Объемы прямой призмы и прямого кругового цилиндра (формулировки, доказательства).
4. Принцип Кавальери (формулировка, примеры).
5. Объем наклонного цилиндра (формулировка, доказательство).
6. Объемы наклонной призмы и наклонного кругового цилиндра (формулировки, доказательства).
7. Теорема об объемах двух конусов с равными высотами и основаниями равной площади (формулировка, доказательство).
8. Объем пирамиды (формулировка, доказательство).
9*. Объем усеченной пирамиды (формулировка, доказательство).
10. Исторические сведения об измерении объемов пространственных фигур.
11. Объем конуса (формулировка, доказательство).
12*. Объем усеченного конуса (формулировка, доказательство).
13. Объем шара (формулировка, доказательство).
14. Объем шарового сегмента (формулировка, доказательство).
15. Понятие площади поверхности многогранника (определение, примеры).
16. Площадь поверхности цилиндра (формулировка, доказательство).
17. Площадь поверхности конуса (формулировка, доказательство).
18. Площадь поверхности усеченного конуса (формулировка, доказательство).
19. Площадь поверхности шара (формулировка, доказательство).
20. Площадь поверхности шарового сегмента (формулировка, доказательство).
Задачи
1. Докажите, что площади боковых поверхностей двух цилиндров, объемы которых равны, относятся как радиусы их оснований.
2. Докажите, что если два цилиндра равновелики, то площади их боковых поверхностей обратно пропорциональны радиусам оснований.
3. Докажите, что объем призмы, основанием которой является трапеция, равен произведению среднего арифметического между площадями параллельных боковых граней на расстояние между ними.
4. В основании четырехугольной призмы лежит ромб. Диагональные сечения перпендикулярны плоскости основания и площади их равны соответственно 100 см2 и 105 см2; длина их линии пересечения равна 10 см. Найдите объем и площадь боковой поверхности данной призмы.
5. Найдите объем параллелепипеда, если площади двух его граней равны P и Q, их общее ребро равно b, двугранный угол между ними равен 300.
6. В треугольной призме площадь одной из ее боковых граней равна m 2, а расстояние от нее до противоположного ребра равно h. Найдите объем призмы.
7. В кубе с ребром a взято 5 точек: центр верхней грани и середины сторон нижней грани. Эти точки служат вершинами многогранника, вписанного в куб. Найдите его объем и площадь поверхности.
8. Основанием пирамиды является правильный шестиугольник со стороной a. Одно из боковых ребер перпендикулярно плоскости основания и равно стороне основания. Найдите объем и площадь боковой поверхности данной пирамиды.
9. Найдите отношения объемов и боковых поверхностей двух цилиндров, один из которых описан около правильной треугольной призмы, а другой вписан в нее.
10. В цилиндре площадь сечения, перпендикулярного оси, равна Q, площадь осевого сечения равна S. Найдите объем цилиндра и площадь его поверхности.
11. На основаниях равностороннего цилиндра, диаметры которых равны 2 дм, построены два конуса с вершинами в середине оси цилиндра. Найдите сумму объемов конусов и сумму площадей их поверхностей.
12. Около конуса с радиусом основания R описана пирамида, у которой периметр основания равен 2 p. Найдите отношение их объемов и отношение площадей их боковых поверхностей.
13. Треугольник со сторонами 10 дм, 17 дм и 21 дм вращается вокруг большей стороны. Найдите объем и площадь поверхности полученного тела.
14. Два конуса имеют образующую одинаковой длины l. Развертки их боковых поверхностей дополняют друг друга до круга. Площади поверхностей относятся как 1:6. Найдите радиусы оснований данных конусов.
15. Конус, имеющий высоту h, радиус основания r, пересечен двумя плоскостями, параллельными его основанию и делящими высоту на три равные части. Найдите объем средней части.
16. Дана четверть круга OABC с центром в точке O и дугой ACB. В ней проведена хорда AB. Докажите, что объемы фигур, которые получаются при вращении треугольника AOB и сегмента ACB вокруг прямой AO, равны.
17. Докажите, что площадь поверхности тела, полученного вращением квадрата вокруг своей стороны, равна площади поверхности шара, радиус которого равен стороне данного квадрата.
18. Около правильной треугольной призмы, у которой высота в два раза больше стороны основания, описан шар. Найдите отношение его объема к объему данной призмы.
19. В шар вписана прямая треугольная призма, стороны основания которой равны 2 дм, 2 дм и 3,2 дм. Найдите площадь поверхности шара.
20. Площадь поверхности шара равна 169 
см2, а образующая вписанного в него конуса равна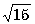 
см. Найдите объем конуса.
