Зачет №1
"Аксиомы стереометрии. Параллельность прямой и плоскости"
Вопросы
1. Основные понятия стереометрии.
2. Аксиомы стереометрии (формулировки, рисунки).
3. Следствия из аксиом стереометрии (формулировки, рисунки).
4. Перечислить способы задания плоскостей
5. Перечислить случаи взаимного расположения прямой и плоскости.
6. Какие прямые в пространстве называются параллельными?
7. Какие прямые называются скрещивающимися?
8. Признаки параллельности прямых в планиметрии (только формулировки и рисунки).
9. Признак параллельности прямых в стереометрии (формулировка, рисунки, доказательство).
10. Что значит: прямая и плоскость параллельны?
11. Признак параллельности прямой и плоскости (формулировка, рисунки, доказательство)
12. Определение угла между прямыми в пространстве (пересекающимися, скрещивающимися и перпендикулярными).
13. Теорема об углах с сонаправленными сторонами (формулировка, рисунок, доказательство).
14.Признак скрещивающихся прямых (формулировка, рисунки, доказательство)
15.Тетраэдр, параллелепипед.
16.Построение сечений.
17Определение перпендикулярных прямых в пространстве.
18.Определение прямой, перпендикулярной плоскости
19.Признак перпендикулярности прямой и плоскости.
Чтобы сдать зачет:
На "5", необходимо сформулировать аксиомы, теоремы, построить чертежи, уметь доказывать теоремы. Решить задачу.
На "4", необходимо сформулировать аксиомы, теоремы, построить чертежи, уметь доказывать теоремы.
На "3", необходимо сформулировать аксиомы, теоремы, построить чертежи.
Примерные задачи к зачету
Задача 1.
| Аа |
| α |
| в |
| C |
| Д |
| К |
| х |
Дано: АВIIα; АВ=7 см
АВК∩α=СД; СД=6 см, СК=8 см
Найти: СД
Задача 2.
| Аа |
| α |
| Вв |
| С |
| М |
| N |
Дано: (А,В) α, с α
М-середина АС
N-середина ВС
Доказать МNIIα
АВ
В
СВ
С1В
А11В
Задача 3. άВ
Дано: ВС=АС,
СС1II АА1,
АА1=22 см
Найти СС1
Задача 4.
| АВ |
| В |
| КСВ |
| К1В |
| А11В |
| άВ |
| В1 |
АА1II КК1IIВВ1;
АА1=10 см,
ВВ1=6 см
Найти:КК1
Задача 5.
Дан куб АВСDA1B1C1D1, т. М лежит на ребре DD1, т. N лежит на ребре CC1, т. K лежит на ребре BB1. Постройте линию пересечения плоскостей MNK и ABC.
 Задача 6. Задача 6.
| 1. Пользуясь данным рисунком, назовите: ü четыре точки, лежащие в плоскости SAB, в плоскости ABC; ü плоскость, в которой лежит прямая MN, прямая КМ; ü прямую, по которой пересекаются плоскости ASC и SBC; ü плоскости SAC и CAB. |
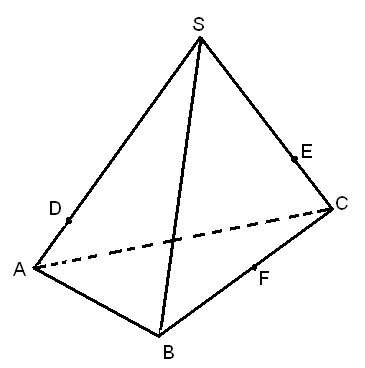 Задача 7. Задача 7.
| 2.Пользуясь данным рисунком, назовите: ü две плоскости, содержащие прямую DE, прямую EF; ü прямую, по которой пересекаются плоскости AEF и SBC, BDE и SAC; две плоскости, которые пересекает прямая SB; AC |
Задача 8.
Точка С лежит на отрезке АВ, причём АВ:ВС=4:3. отрезок CD, равный 12см, параллелен плоскости α, проходящей через точку В. Докажите, прямая AD пересекает плоскость α в некоторой точке Е, и найдите отрезок ВЕ.
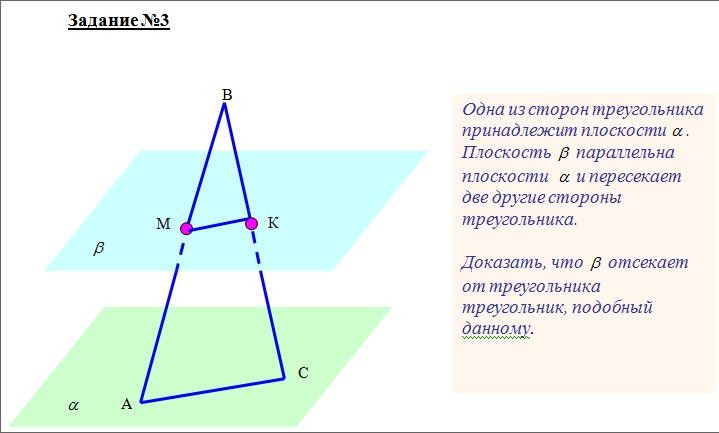
Задача 9. Сторона АС треугольника АВС параллельна плоскости α, а стороны АВ и ВС пересекаются с этой плоскостью в точках М иN. Докажите, что  АВС ~
АВС ~  МВN.
МВN.
Готовимся к зачету
Зачет №1
 Тема «Аксиомы стереометрии и их простейшие свойства»
Тема «Аксиомы стереометрии и их простейшие свойства»
1.Сформулировать аксиомы стереометрии.
2. Сформулировать следствия из аксиом стереометрии.
3. Перечислить способы задания плоскостей
4. Перечислить случаи взаимного расположения прямой и плоскости.
| № п/п | Вопросы | Ответы |
| Через сколько точек можно провести прямую? |
| |
| Как пересекаются плоскости? |
| |
| Если две прямые имеют общую точку, то через них можно провести только … |
| |
| Что такое аксиома? |
| |
| Сколько прямых можно провести через две точки? |
| |
| Что может принадлежать плоскости? |
| |
| Что может принадлежать прямой? |
| |
| Теорема – это утверждение… |
| |
| Прямые называются параллельными, если они… |
| |
| Примеры параллельных прямых. |
|

| 1. Пользуясь данным рисунком, назовите: ü четыре точки, лежащие в плоскости SAB, в плоскости ABC; ü плоскость, в которой лежит прямая MN, прямая КМ; ü прямую, по которой пересекаются плоскости ASC и SBC; ü плоскости SAC и CAB. |

| 2.Пользуясь данным рисунком, назовите: ü две плоскости, содержащие прямую DE, прямую EF; ü прямую, по которой пересекаются плоскости AEF и SBC, BDE и SAC; две плоскости, которые пересекает прямая SB; AC |
Зачет № 2
Тема «Параллельность прямых и плоскостей. Параллельность плоскостей»
1. Какие прямые в пространстве называются параллельными?
2. Какие прямые называются скрещивающимися?
3. Признаки параллельности прямых в планиметрии.
4. Признак параллельности прямых в стереометрии.
5. Что значит: прямая и плоскость параллельны?
6. Признак параллельности прямой и плоскости.
7. Признак скрещивающихся прямых.
8. Перечислить случаи взаимного расположения прямых в пространстве.
9. Какие плоскости называются параллельными?
10. Перечислить случаи взаимного расположения плоскостей в пространстве.
11. Признак параллельности плоскостей.
12. Свойства параллельных плоскостей.
13. Тетраэдр и параллелепипед.
14. Свойства параллелепипеда.
15. Построение сечений.
16. Известно, что прямая параллельна плоскости.
а) Параллельна ли она любой прямой, лежащей в этой плоскости?
б) Может ли она пересечь хотя бы одну из таких прямых?
17. Верно ли утверждение, что плоскости параллельны, если:
а) Прямая, лежащая в одной плоскости, параллельна прямой другой плоскости;
в) Две пересекающиеся прямые, лежащие в одной плоскости соответственно параллельны двум прямым другой плоскости.
Задачи: 1.Основание AD трапеции ABCD лежит в плоскости a. Через точки B и C проведены параллельные прямые, пересекающие плоскость а в точках E и F соответственно.
· Каково взаимное расположение прямых EF и AB?
· Чему равен угол между прямыми EF и AB, если ABC = 150°? Ответ обоснуйте.
2. Изобразите параллелепипед ABCDA 1 B 1 C 1 D 1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер AB, BC и DD 1.

| 
|

|
Зачет № 3
Тема «Перпендикулярность прямых и плоскостей»
1. Определение перпендикулярных прямых в пространстве.
2. Определение прямой, перпендикулярной плоскости.
3. Признак перпендикулярности прямой и плоскости.
4. теорему о трех перпендикулярах,
5. определение перпендикулярных плоскостей,
6. признак перпендикулярности плоскостей,
7. определение угла между прямой и плоскостью,
8. определение двугранного угла,
9. понятие линейного угла двугранного угла,
10. Из данных утверждений верным является:
- Если две прямые перпендикулярны одной прямой, то они параллельны.
- Прямая перпендикулярна плоскости, если она перпендикулярна двум прямым, лежащим в этой плоскости.
- Если прямая, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна линии их пересечения, то она перпендикулярна и другой плоскости.
11. В треугольнике АКС, АК  СК, точка М не принадлежит плоскости АКС и МК
СК, точка М не принадлежит плоскости АКС и МК  СК.
СК.
Какие высказывания верны?
1) АК  СКМ
СКМ
2) СК  АКМ
АКМ
3) АК  МК
МК
4) СК  АМ
АМ
12.Точка М равноудалена то всех вершин прямоугольного треугольника, катеты которого равны 6 см и 8 см Расстояние от точки М до плоскости треугольника равно 12 см. Расстояние от точки М до вершин треугольника равно

8. Прямые а и b – параллельны и лежат в плоскости α. Через каждую из этих прямых проведена плоскость, перпендикулярная α. Каково взаимное расположение полученных плоскостей?
Ответ: 1) пересекаются; 2) совпадают; 3)параллельны.
КОНТРОЛЬНЫЕ РАБОТЫ ПО ГЕОМЕТРИИ 10 класс.
Контрольная работа №1 тема «Параллельность прямых и плоскостей»
В1
1. Даны трапеция АВСД с основанием АД и ВС, и точка М, не лежащая в плоскости этой трапеции. Докажите, что прямая АД параллельна плоскости треугольника ВМС
(В. 2. середины сторон СК и ЕК треугольника СЕК лежат в плоскости α, а сторона СЕ не лежат в этой плоскости. Докажите, что прямая СЕ параллельна плоскости α.)
2. В.1 В тетраэдре АВСД точки М,К,Р – середины ребер АВ,ВС,и ВД. Докажите, что плоскость МКР параллельна плоскости АДС и вычислите площадь треугольника МКР, если площадь треугольника АДС равна 48 кв. см
(В 2. В тетраэдре ДАСВ точки К,Е,М – середины ребер АС,ДС,ВС. Докажите, что плоскости КЕМ и АДВ параллельны, и вычислите площадь треугольника АДВ, если площадь треугольника КЕМ равна 27кв.см
3. В1. Дан параллелепипед  . Точка М лежит в плоскости грани
. Точка М лежит в плоскости грани  и
и 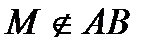
Построить сечение параллелепипеда плоскостью, проходящей через точку М параллельно АВС
(В2. Дан параллелепипед  . Точка Р лежит в плоскости грани
. Точка Р лежит в плоскости грани  и
и 
Построить сечение параллелепипеда плоскостью, проходящей через точку Р параллельно  .
.
Контрольная работа №2 по теме «Перпендикулярность прямых и плоскостей»
В1
1. Через вершину К треугольника ДКF проведена прямая КМ, перпендикулярная к плоскости этого треугольника. Известно, что КМ=15см.  ,
, 
Найти расстояние от точки М до прямой ДF.
2. Дан прямоугольный параллелепипед  Найти двугранный угол
Найти двугранный угол  , если известно, что четырехугольник АВСД – квадрат. АС=
, если известно, что четырехугольник АВСД – квадрат. АС= 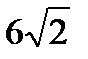 см,
см, 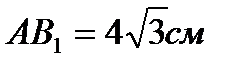
В-2
1.через вершину прямого угла С равнобедренного треугольника СДЕ проведена прямая
СF, перпендикулярная к его плоскости. Найти расстояние от точки F до прямой ДЕ, если СF=16см, 
2.Дан прямоугольный параллелепипед  Найти двугранный угол
Найти двугранный угол 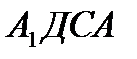 , если известно, что АС=13см,
, если известно, что АС=13см, 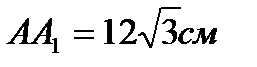 , ДС=5см.
, ДС=5см.
Зачет №1 Геометрия 10 кл.
АКСИОМЫ СТЕРЕОМЕТРИИ.
ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
№1
- Сформулируйте аксиомы стереометрии.
- Докажите признак параллельности прямой и плоскости.
- Через прямые а и в нельзя провести одну плоскость. Могут ли они пересекаться?
- Прямая РО, не лежащая в плоскости АВС, параллельна стороне АВ параллелограмма АВСD. Выясните взаимное расположение прямых РО и АD и найдите угол между ними, если угол АDС равен 1450.
- Параллелограммы АВСD и АВС1 D1 лежат в разных плоскостях. Докажите, что четырехугольник СDD1C1 - параллелограмм.
№2
- Перечислите случаи взаимного расположения прямых в пространстве. Приведите примеры соответствующих прямых на модели куба.
- Докажите признак параллельности двух плоскостей.
- Прямые АВ и СК пересекаются. Могут ли прямые АС и ВК быть скрещивающимися?
- В треугольнике АВС середины сторон АВ и ВС лежат в плоскости
 , а сторона АС не лежит в этой плоскости. Докажите, что прямая АС параллельна плоскости
, а сторона АС не лежит в этой плоскости. Докажите, что прямая АС параллельна плоскости  .
. - Точки А и С лежат в плоскости
 , ЕК параллельна этой плоскости. Найдите длину отрезка АС, если ЕК = 5см и
, ЕК параллельна этой плоскости. Найдите длину отрезка АС, если ЕК = 5см и 
№3
- Какие прямые в пространстве называются параллельными? Приведите примеры.
- Докажите, что если одна из двух параллельных прямых параллельна данной плоскости, а другая имеет с плоскостью общую точку, то эта прямая лежит в данной плоскости.
- Прямые а и с параллельны, а прямые в и с пересекаются. Могут ли прямые в и с быть параллельными?
- Прямая q, не лежащая в плоскости АВС, параллельна основанию АD трапеции ABCD. Выясните взаимное расположение прямых q и CD и найдите угол между ними, если
 .
. - Точка Е не лежит в плоскости параллелограмма АВСD. Докажите, что прямая проходящая через середины отрезков ЕА и ЕВ, параллельна стороне СD параллелограмма
№4
- Какие прямые называются пересекающимися? Приведите примеры таких прямых на модели тетраэдра.
- Докажите, что две прямые, параллельные третьей, параллельны между собой.
- Даны параллельные прямые а и в и плоскость
 , проходящая через прямую в. Пересекает ли прямую а плоскость
, проходящая через прямую в. Пересекает ли прямую а плоскость  ?
? - Три отрезка АА1, ВВ1, СС1, не лежащие в одной плоскости, имеют общую середину – точку О. Докажите. Что плоскости АСВ и А1 С1В1 параллельны.
- .Плоскость
 проходит через вершины В и С треугольника АВС, но не совпадает с плоскостью этого треугольника. На сторонах АВ и АС треугольника взяты соответственно точки К и Е так, что ЕК = 6 см и параллелен плоскости
проходит через вершины В и С треугольника АВС, но не совпадает с плоскостью этого треугольника. На сторонах АВ и АС треугольника взяты соответственно точки К и Е так, что ЕК = 6 см и параллелен плоскости  ,
,  . Найдите длину отрезка ВС
. Найдите длину отрезка ВС
№5
- Перечислите случаи взаимного расположения прямой и плоскости в пространстве.
- Докажите. что отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
- Могут ли две плоскости иметь: а) только одну общую точку; б) только две общие точки; в) только одну общую прямую? Ответ обоснуйте.
- Из точки К проведены до пересечения с плоскостью
 три луча. Точки пересечения лучей с плоскостью соединены отрезками АВ = 6 см, СВ = 8 см. СА = 10 см. Найдите длину ломаной, проходящей через середины отрезков КА, КВ, КС.
три луча. Точки пересечения лучей с плоскостью соединены отрезками АВ = 6 см, СВ = 8 см. СА = 10 см. Найдите длину ломаной, проходящей через середины отрезков КА, КВ, КС. - Постройте сечение куба АВСDА !В1С! D1 плоскостью, проходящей через ребра АВ и С! D1. Какая фигура получилась в сечении?
№6
- Какие прямые в пространстве называются скрещивающимися? Приведите примеры на модели параллелепипеда.
- Докажите, что если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
- Верно ли утверждение: две прямые параллельные некоторой плоскости, параллельны друг другу.?
- В тетраэдре АВСD точки M,N,P,K – середины соответствующих отрезков AC, AB, DВ и DC. Найдите периметр четырехугольника MKNP, если BC = 10см, AD =16см.
- Постройте сечение тетраэдра ABCD плоскостью проходящей через точки А, E, F, если точки E, F принадлежат ребрам DB BC соответственно.
№7
- Какие прямая и плоскость называются параллельными? Приведите примеры на модели куба.
- Докажите признак скрещивающихся прямых.
- Точка К не лежит в плоскости прямоугольника АВСD. Как расположена прямая СD по отношению к плоскости АВК? Ответ обоснуйте.
- В тетраэдре АВСD точки М, К, Р – середины ребер АВ, АС, ВD. Докажите, что плоскость МКР параллельна плоскости АСD. Вычислите площадь треугольника МРК, если площадь треугольника АСD равна 56 см2
- В кубе АВСDА!В1С! D1 проведите сечение плоскостью через ребро СС1 и прямую, проходящую через точку пересечения диагоналей грани АА1DD1.
№8
- Какие плоскости называются параллельными? Приведите примеры на моделях геометрических тел.
- Докажите, что если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
- Могут ли скрещивающиеся прямые а и в быть параллельными прямой с? Ответ обоснуйте.
- Через точки А, В и середину М отрезка АВ проведены параллельные прямые пересекающие некоторую плоскость
 в точках А1, В1, М1 соответственно. Найдите длину отрезка АА1, если ММ1 = 10 см, ВВ1 = 8 см, причем отрезок АВ не пересекает плоскость
в точках А1, В1, М1 соответственно. Найдите длину отрезка АА1, если ММ1 = 10 см, ВВ1 = 8 см, причем отрезок АВ не пересекает плоскость  .
. - Постройте сечение параллелепипеда АВСDА !В1С! D1 плоскостью АВС1
Темы: «Аксиомы стереометрии и следствия из них»






