Углы и треугольники
Углы, измерение углов. Виды углов. Смежные углы, их свойство. Вертикальные углы, их свойства.
Угол – геометрическая фигура, состоящая из точки и двух лучей, выходящих из этой точки. Угол делит плоскость на две части: внутреннюю и внешнюю области угла.
Градус – угол, равный 180 части развернутого угла.
Развернутый угол – угол, обе стороны которого лежат на одной прямой.
Смежные углы – 2 угла, у которых одна сторона общая, а две другие являются продолжениями друг друга. Сумма градусных мер смежных углов равна 180 градусов.
Вертикальные углы – углы, в которых стороны одного угла являются продолжениями другого. Вертикальные углы равны, что доказывается через свойство смежных углов.
Треугольники, их виды по углам и сторонам.
Треугольник – геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и отрезков, соединяющих эти точки.
Остроугольный треугольник – треугольник, в котором все углы острые.
Прямоугольный треугольник – треугольник, в котором один угол прямой, а два остальных – острые.
Тупоугольный треугольник – треугольник, в котором один угол тупой, а два других – острые.
Равнобедренный треугольник – треугольник, две стороны которого равны между собой.
Равносторонний треугольник – треугольник, все стороны которого равны.
Признаки равенства треугольников.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.
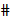1.Рассмотрим треугольники ABC и А1В1С1, у которых АВ = А1В1, АС = А1С1, углы А и А1 равны. Докажем, что ABC и А1В1С1 равны.
2.Так как угол А равен углу А1, то треугольник АВС можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1С1 и А1С1 соответственно.
3.Поскольку АВ = А1В1 и АС = А1С1, то при наложении АВ совместится со стороной А1В1, а сторона АС – со стороной А1С1; в частности, совместятся точки А и А1, В и В1, следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны, 
.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне двум прилежащим к ней углам другого треугольника, то эти треугольники равны.
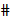1. Рассмотрим треугольники ABC и А1В1С1, у которых АВ = А1В1, углы А и А1, В и В1 соответственно равны.
2.Наложим треугольник АВС на треугольник А1В1С1 так, чтобы вершина А совместилась с вершиной А1, сторона АВ – с равной ей стороной А1В1, а вершины С и С1 оказались бы по одну сторону от прямой А1В1.
3.Так как углы А и А1, В и В1 соответственно равны, то сторона АС наложится на луч А1С1, а сторона ВС – на луч В1С1. Следовательно, вершина С – общая точка сторон АС и ВС – окажется лежащей как на луче А1С1, так и на луче А1В1 и совместится с общей точкой этих лучей – вершиной С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, поэтому они равны, .
