Построить круговой конус со сквозным поперечным вырезом или окном в трех проекциях. Диаметр основания конуса 90 мм, высота 100 мм. Данным к задаче 7.1. приведены в табл. 4; пример выполнения — на рис. 5.
_______________
* В качестве вариантов задач выполняют задачу 7.1 или 7.2 или их комбинацию.
Решение. Круговой конус — поверхность второго порядка. Плоскость, не проходящая через его вершину, пересекает конус по окружности, эллипсу или параболе, если она расположена по одну сторону от вершины, и по гиперболе, если она пересекает его по обе стороны от вершины.
Таблица 4. Задача 7.1
 |
Продолжение табл. 4
 |
 Продолжение табл. 4
Продолжение табл. 4

Рис. 6
Перед выполнением задания устанавливают, какие линии получаются при пересечении конуса каждой из плоскостей. Горизонтальную и профильную проекции линий пересечения строят по точкам. При этом обязательно отмечают характерные точки, например большую и малую оси эллипсов, точки касания кривых проекций очерков, вершины кривых, точки на границах видимости. Построив ряд точек, соединяют их плавной линией и обводят по лекалам, желательно цветным фломастером или карандашом. При обводке особое внимание следует обратить на форму кривой — эллипса.
Следы вспомогательных секущих плоскостей и точки линий пересечения следует обозначить, линии построений — сохранить.
ЗАДАЧА 7.2 (лист 4). СФЕРА С ВЫРЕЗОМ (ИЛИ ОКНОМ). Построить сферу радиусом R = 50 мм со сквозным поперечным вырезом (окном) призматической формы в трех проекциях. Фронтальная проекция А" В" С" D" сквозного окна дана четырехугольником. Данные к задаче 7.2 приведены в табл. 5; пример выполнения — на рис. 6.
Таблица 5. Данные к задаче 7.2
| Вариант | О | А | В | C,D | ||||
| x | y | z | x | z | x | z | x | |
Значения: для В и С, для А и D — z одинаковы.
Решение. Намечают оси координат и строят проекции сферы диаметром 100 мм с центром в заданной точке О. По заданным координатам строят фронтальную проекцию сквозного отверстия в сфере, определяют характерныe точки линий сквозного отверстия, точки на экваторе, главном меридиане, наиболее удаленные и ближайшие точки поверхности сферы к плоскостям проекций, точки концов большой и малой осей эллипсов, точки касания кривых проекций очерков. При обводке особое внимание следует обращать на форму кривой эллипса.
Следы вспомогательных секущих плоскостей и точки линий пересечения следует обозначить, линии построения — сохранить.
ЗАДАЧА 8 (лист 4). ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ. Построить линию пересечения поверхностей заданных непрозрачных фигур (тел). Варианты данных к задаче приведены в табл. 6. Пример выполнения — на рис 5.
Решение. По размерам, приведенным в табл. 4 для заданного варианта, начертить в тонких линиях две проекции заданных поверхностей. Проекции линий пересечения поверхностей строят по точкам с помощью вспомогательных секущих плоскостей или сфер.
Таблица 6. Задача 8
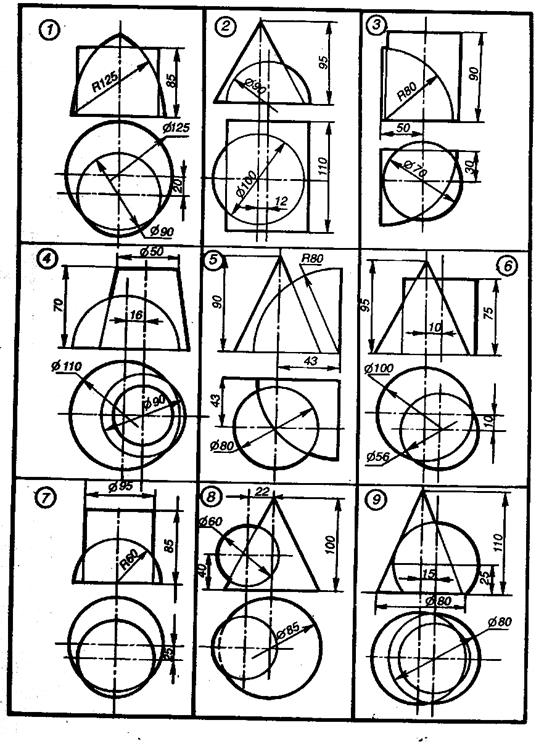
Продолжение табл. 6
 |
Вспомогательные секущие поверхности (плоскости или сферы) выбирают так, чтобы они пересекали поверхности по наиболее простым линиям (прямые, окружности). В первую очередь определяют опорные (характерные) точки: точки, принадлежащие очеркам поверхностей и их экваторам, высшую и низшую точки и др. Обозначают вспомогательные секущие поверхности и проекции точек линии пересечения. Построенные точки плавно соединяют с учетом их видимости и обводят цветным карандашом или фломастером. Проекции заданных поверхностей обводят черным карандашом. При обводке следует обратить внимание на то, что пересекающиеся между собой фигуры образуют одно тело.
ЗАДАЧА 9 (лист 5). РАЗВЕРТКА ЛИНЕЙЧАТОЙ ПОВЕРХНОСТИ. Построить развертку линейчатой поверхности в задаче 8. Если обе пересекающиеся поверхности линейчатые, строят развертку конуса. Пример выполнения приведен на рис. 7.
 |
Рис. 7
Решение. Все вспомогательные графические построения для выполнения развертки поверхности конуса или цилиндра выполнить в тонких линиях в задаче 8. Развертка цилиндра вращения состоит из развертки его боковой поверхности и двух оснований. На развертке боковой поверхности цилиндра строят развертку линии его пересечения с конусом. Для этого проводят прямолинейные образующиеся, проходящие через характерные точки линии пересечения цилиндра с конусом, и отмечают на них эти точки. Через отмеченные точки с помощью лекал проводят линию пересечения. Она симметрична относительно средней линии цилиндра. Построенную линию обводят цветным карандашом или фломастером. Внешний очерк развертки обводят простым карандашом.
Развертка боковой поверхности конуса вращения — круговой сектор с углом α = R × 360/L, где R — радиус окружности основания конуса вращения, L -длина образующей. Этот сектор можно построить с достаточной для критических целей точностью следующим образом. Основание делят, например на 12 частей, и по частям отмечают его на окружности радиуса L.
На развертке конуса строят прямолинейные образующие или параллели, проходящие через характерные точки линии пересечения конуса с цилиндром. Через построенные точки с помощью лекал проводят плавную линию пересечения и обводят ее цветным карандашом или фломастером.






