Вольтамперная характеристика идеального p-n перехода

*Уравнение непрерывности заряда является выражением общего закона неопределённости в физике.

Его физический смысл состоит в том, что заряды некоторой области не могут возникать или исчезать

за бесконечно короткие промежутки времени, т.к. на это требуется бесконечно большая энергия.

Применительно к решаемой нами задаче, для идеализированного перехода уравнение непрерывности приводится к следующим выражениям, которые называются уравнениями диффузии.

Для количественного определения токов через переход уравнения диффузии для электронов и дырок соответственно, решаются совместно с приведёнными ранее уравнениями плотности токов.

j_{n диф.} = q·D_n· ∂ n_p/ ∂x j_{p диф.} = -q·D_p· ∂ p_n/ ∂x

Где: D_n и D_p – коэффициенты диффузии, Δn_p и Δp_n – граничные концентрации, τ_n и τ_p – время жизни

электронов и дырок соответственно, x – расстояние, отсчитываемое от границы p-n перехода вглубь области электронного или дырочного полупроводника.

Окончательное решение этих уравнений имеет вид:

где L_n и L_p – диффузионная длина электронов и дырок соответственно, т.е. расстояние на котором соответствующая концентрация в результате рекомбинации убывает в e раз (прибл. в 2,7 раз).

Подставляя выражения для концентраций в уравнения плотности токов, получим:

Хотя, как следует из этих выражений, j_{n диф} и j_{p диф} зависят от x, общий ток p-n перехода постоянен в любом сечении полупроводника. Вблизи границ перехода, при x=0, этот ток практически диффузионный, поэтому он может быть найден как сумма j _диф = j_{n диф} + j_{p диф} при x=0.

Соответственно, ток I через p-n переход площадью S равен

I = j · S. Подставив в эту формулу найденное значение плотности тока, получим

Как следует из этого выражения, ток I через p-n переход является экспоненциальной функцией приложенного к нему напряжения U и температуры T (φ_T = k·T/q). Кроме того, при U = const, величина тока определяется параметрами S, D_n, D_p, L_n, L_p, p_n0, n_p0, характеризующими геометрию перехода, материал полупроводников, концентрацию неосновных носителей и концентрацию примесей (степень легирования). Поэтому коэффициент при экспоненте удобно выделить, обозначив его как I ₀.

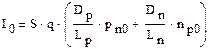
где

 

Статическая вольтамперная характеристика p-n перехода

Проанализируем выражение для тока I ₀. Учитывая, что

получим:

Поскольку n_i² ≈ e^-Δφ_з^·q/k·T

где Δφ_з – ширина запрещённой зоны,

то 1) - этот ток будет сильно зависеть от температуры, поэтому его часто называют тепловым. 2) – этот ток будет тем меньше, чем больше ширина запрещённой зоны Δφ_з.

Например, у кремния ширина запрещённой зоны Δφ_з = 1,12В, а у германия Δφ_з = 0,66В. Поэтому абсолютное значение теплового тока кремниевого перехода на несколько порядков меньше соответствующего тока германиевого перехода. Однако, по той же причине, относительное изменение теплового тока кремниевого перехода значительно больше чем у германиевого. В этом можно убедиться взяв производную d n _i /d T.

 

На рисунке дано качественное сравнение вольтамперных характеристик германиевого и кремниевого переходов, при различных температурах. Прямая ветвь вольтамперной характеристики кремниевого перехода как бы сдвинута вправо (обычно на 0,3 – 0,4В) относительно ВАХ германиевого перехода,

т.к. величина I ₀, входящая масштабным множителем в выражение для тока, у кремниевых переходов на несколько порядков меньше, чем у германиевых. По той же причине обратный ток в кремниевом переходе на несколько порядков меньше, чем у германиевого. Как прямой, так и обратный токи p-n перехода возрастают с увеличением температуры, причём относительное изменение тока у кремниевого перехода выражено сильнее.