Суммарная протяжённость p-n перехода, в обе стороны от границы раздела, называется шириной p-n перехода l 0. l 0 = l p + l n, где l p и l n – ширина p-n перехода, соответственно в p и n областях.
Выясним, чем определяется ширина p-n перехода и протяжённость её участков l n и l p в n и p областях. Для этого рассмотрим зонную диаграмму контакта двух полупроводников.
Здесь мы перешли от энергетической зонной диаграммы к потенциальной зонной диаграмме имея ввиду, что φ = W/q. Так удобнее для дальнейшего
рассмотрения процессов происходящих в p-n переходе при подключении к нему внешнего источника напряжения.
Так как уровень Ферми по определению не может быть разным в n и p полупроводниках, валентные зоны и зоны проводимости в них оказываются на разных потенциальных уровнях. Следовательно середины запрещённых зон в n и p областях смещены
относительно друг друга на величину
φк 0 = φEp – φEn
Эта величина называется контактной разностью потенциалов p-n перехода или его потенциальным барьером в равновесном состоянии.
Ранее были приведены выражения: 
Разрешив их относительно φEp и φEn и учитывая, что nn · pn = ni2, в общем случае получим:
Отсюда следует, что контактная разность потенциалов в p-n переходе определяется отношением концентраций одноимённых носителей заряда, т.е. отношением концентрации основных носителей заряда одной области к концентрации неосновных носителей заряда другой области. В частности для равновесного состояния:
Типичная величина потенциального барьера, при температуре близкой к комнатной, составляет для германиевого перехода 0,35 – 0,4В, а для кремниевого 0,65 – 0,7В.
Электрическое поле в p-n переходе определяется на основании уравнения Пуассона:
dE/dx = Q(x)/ε·ε 0, где ε – диэлектрическая проницаемость среды, а ε 0 – вакуума.
Полагая, что примеси распределены в основных полупроводниках равномерно можно считать, что
Qp(x) = -q·Nа; -l p ≤ x ≤0, для p – области и Qд(x) = +q·Nд; 0 ≤ x ≤ l n, для n – области.
Тогда интегрируя уравнение Пуассона в соответствующих пределах, получим:
При других значениях x E = 0.
Приравнивая E p(0) и E n(0), получим:
l p / l n = N а / N д.
Следовательно, протяжённость объёмного заряда от границы раздела вглубь полупроводника, обратно пропорциональна
степени его легирования. Объёмные заряды по обе стороны границы раздела должны уравновешивать друг друга.
 |
По определению напряженность поля E(x) = -dφ(x)/dx, следовательно интегрируя эти выражения можно определить закон изменения потенциала в p – n переходе.
Зависимости Q(x), E(x) и φ(x) приведены на рисунке.
Приравнивая φn(0) и φp(0) и учитывая, что
φк 0 = φEp – φEn найдём:
 |  | ||
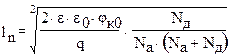Если ln = l p переход называется симметричным, при ln < l p или ln > l p несимметричным.
Симметричные переходы получаются при Nа = Nд, в противном случае они несимметричные.
Если контакт полупроводников идеальный, как это определялось выше, и, к тому же, ширина p-n перехода пренебрежимо мала по сравнению с линейными размерами его площади, то такой p-n переход считается близким к идеальному. Рассмотренный нами p-n переход относится к так называемым ступенчатым или резким переходам из-за резкого характера изменения концентрации примесей одного элемента на другой. Плавными называют переходы в которых переход на границе раздела от примеси одного элемента к другой примеси происходит плавно.
Современные технологии и оборудование позволяют получать p-n переходы близкие к резкому,
поэтому при дальнейшем изучении процессов, происходящих в p-n переходах, будем считать их резкими.
