Разрешенные зоны содержат большое количество уровней, на каждом из которых могут находиться электроны. Чтобы оценить фактическую концентрацию носителей в полупроводнике, необходимо знать распределение уровней и вероятность их заполнения.
Для невырожденных полупроводников вероятность заполнения уровня W в зоне проводимости дается распределением Максвела–Больцмана:
,
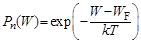где W F – энергия, характеризующая уровень Ферми, т.е. уровень, вероятность заполнения которого равна 0,5; k = 1,38 · 10–23 Дж/ºК – постоянная Больцмана, Т – температура по шкале Кельвина.
Вероятность незаполнения уровня в валентной зоне, т.е. наличия дырки на этом уровне, определяется аналогично:
.
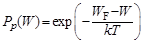В предположении того, что плотность уровней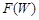 
~ 
,
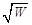концентрация свободных электронов будет равна:
,
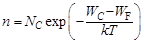где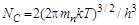 
, mn – эффективная масса электрона,
h = 6,63 · 10–34 Дж · С – постоянная Планка.
Аналогично концентрация дырок
,
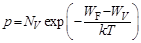где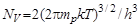 
, mp – эффективная масса дырки.
Из произведения концентраций:
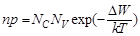
видно, что при неизменной температуре произведение концентраций – величина постоянная. Увеличение одной из концентраций сопровождается уменьшением другой.
В собственном полупроводнике концентрации электронов и дырок одинаковы: ni = pi (здесь и далее символ i означает собственный полупроводник). Поэтому
.
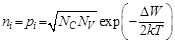Из этого выражения следует:
1) собственная концентрация носителей заряда очень сильно зависит от ширины запрещенной зоны. Именно поэтому значение ni для кремния на три порядка меньше, чем для германия;
2) собственная концентрация очень сильно зависит от температуры. При этом влияние температуры тем сильнее, чем больше ширина запрещенной зоны.
Для примесных полупроводников справедливы следующие выражения:
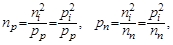
где np, pp – концентрации электронов и дырок в полупроводнике
р -типа; nn, pn – концентрация электронов и дырок в полупроводнике
n -типа.
С учетом того, что
, 
, 
, 
,
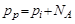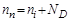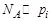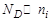где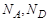 
– концентрации акцепторных и донорных примесей, получим:
, 
, 
, 
.
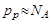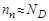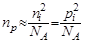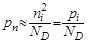Отсюда вывод: концентрация неосновных носителей заряда в полупроводнике обратно пропорциональна концентрации примеси.
Важными характеристиками полупроводника являются скорость генерации V ген и скорость рекомбинации V рек электронно-дырочных пар:
, 
,
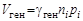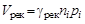где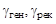 
– коэффициенты, зависящие от материала полупро-
водника.
Равновесное состояние полупроводника характеризуется тем, что скорость генерации равна скорости рекомбинации: V ген = V рек.
Неравновесным состоянием полупроводника называется такое состояние, когда скорость генерации отличается от скорости рекомбинации: V ген 
V рек.
Зная концентрацию электронов и дырок, можно определить значение уровня Ферми:
,
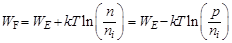где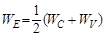 
– электростатический потенциал полупроводника.
Отсюда можно сделать следующие выводы.
1. В собственных полупроводниках, у которых n = p = ni, уровень Ферми расположен в середине запрещенной зоны.
2. В электронных полупроводниках (n -типа), у которых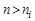 
, уровень Ферми лежит в верхней половине запрещенной зоны и тем выше, чем больше концентрация электронов.
3. В дырочных полупроводниках (р -типа), у которых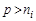 
, уровень Ферми лежит в нижней половине запрещенной зоны и тем ниже, чем больше концентрация дырок.
4. С ростом температуры, когда примесный полупроводник постепенно превращается в собственный, уровень Ферми смещается к середине запрещенной зоны.
Одно из фундаментальных положений в физике полупроводников формулируется следующим образом: уровень Ферми одинаков во всех частях равновесной системы, какой бы она ни была.
