В качестве такой модели наибольшее распространение получила модель Эберса-Молла, которая основывается на уравнении диода (уравнении Шокли). Эта модель при достаточно высокой точности является наименее сложной (содержит минимальное количество элементов с легко измеряемыми параметрами).
Общая эквивалентная схема транзистора, используемая при получении математической модели Эберса-Молла, показана на писунке.
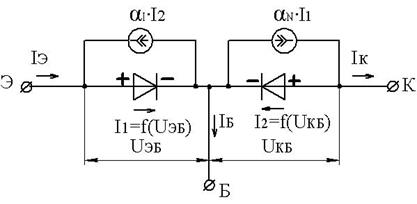
Каждый переход транзистора p-n-p типа представлен в виде диода, а их взаимодействие отражено генераторами токов, где:
αI – инверсный коэффициент передачи тока (из коллектора в эмиттер);
αN – нормальный коэффициент передачи тока (из эмиттера в коллектор)
αNI1 – генератор коллекторного тока при нормальном включении;
αII2 – генератор эмиттерного тока при инверсном включении.
Таким образом, токи эмиттера и коллектора в общем случае содержат две составляющие: инжектируемую (αI или αN) и экстрактируемую (αNI1или
αII2), поэтому:
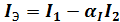; (1)
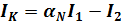(2)
Если в общей эквивалентной схеме поочередно прикладывать напряжение к каждому p-n переходу, а выводы других, соответственно, поочередно замыкать между собой накоротко, то токи I1и I2, протекающие через p-n переходы к которым приложено напряжение (в соответствии с уревнением Шокли) примут вид:
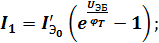(3)
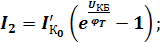(4)
где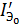 
- тепловой ток эмиттерного p-n перехода при замкнутых базе и коллекторе;
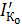- тепловой ток коллекторного p-n перехода при замкнутых базе и эмиттере.
−n переходов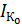 
, 
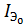, включенных раздельно и тепловыми токами 
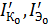получим из (1) и (2).
Пусть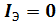 
, тогда 
.
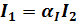При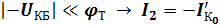 
.
Подставив эти выражения в (1) и (2) для тока коллектора получим:
,
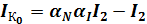учитывая, что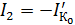 
имеем:
,
;
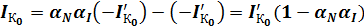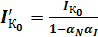Аналогично: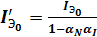 
.
Токи коллектора и эмиттера с учетом (3) и (4) будут:
;
;
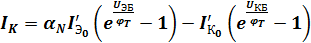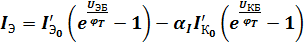На основании закона Кирхгофа ток базы будет: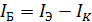 
;
.
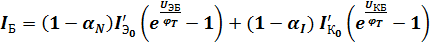В самом общем случае в транзисторах справедливо равенство:
,
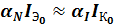тогда при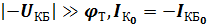 
,
поэтому
.
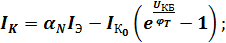
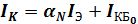Последние уравнения описывают выходные ВАХ транзистора.
Из уравнения для определения IЭ, решенное относительно UЭБ, получим выражение для идеализированных входных характеристик транзистора:
.
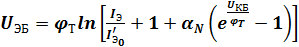Учитывая, что обычно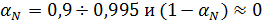 
, последнее уравнение может быть упрощено:
.
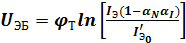Модели Эберса-Молла, несмотря на их приближенность, очень полезны для анализа статических режимов при больших изменениях сигналов, так как они нелинейные.
Модели транзистора в режиме малого сигнала
Динамический режим).
При анализе работы биполярного транзистора в качестве усилительного прибора, когда напряжение база-эмиттер изменяется во времени периодически и амплитуда этого напряжения достаточно мала по сравнению с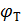 
, эквивалентные схемы для такого сигнала целесообразно линеаризовывать. Такие эквивалентные схемы часто называют малосигнальными.
Поэтому транзистор в режиме малого сигнала можно рассматривать как линейный активный четырёхполюсник (см.рисунок), для которого существуют два уравнения, связывающие между собой физические величины:
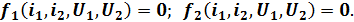
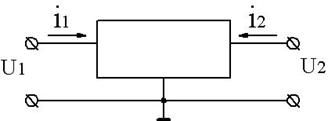
Биполярный транзистор, как четырёхполюсник.
В данных уравнениях две переменные могут быть независимыми, а две другие выражаться через них. При этом потребуются четыре коэффициента, играющих роль независимых параметров.
Коэффициенты в уравнениях четырёхполюсника называются характеристическими параметрами.
Возможны шесть способов представления функциональных зависимостей между токами и напряжениями транзистора:
1) 
2) 
3) 
4) 
5) 
6) 
На практике наиболее часто используются три вида соотношений:1),2),3).
1) - соответствует параметрам холостого хода (z-параметры);
2) - соответствует параметрам короткого замыкания (y-параметры);
3) - соответствует гибридным (смешанным) параметрам (h-параметры).
Определяя полные дифференциалы функций из уравнений 1),2),3) будем иметь:
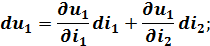
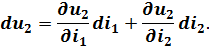
Вводя новые обозначения для частных производных, имеющих размерность сопротивлений, и заменяя дифференциалы токов и напряжений, получим:
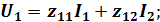
Z-параметры имеют размерность сопротивлений.
Из уравнения 2) получим:
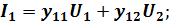
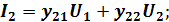
y-параметры имеют размерность сопротивлений.
Из уравнения 3) получим:
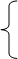
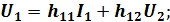
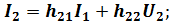
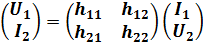
h-параметры – гибридные параметры.
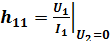– входное сопротивление в режиме короткого замыкания выхода; (по переменному току);
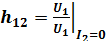– коэффициент обратной связи по напряжению при холостом ходе на входе;
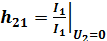–коэффициент передачи тока (коэффициент усиления) при коротком замыкании на выходе;
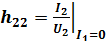– выходная проводимость на холостом ходе на входе.
Эквивалентная схема, соответствующая системе h-параметров:
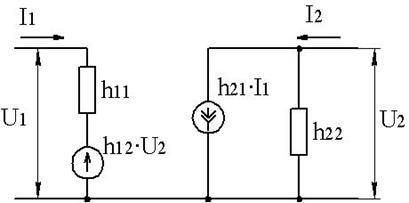
Между h-параметрами и параметрами транзистора, соответствующими Т-образным эквивалентным схемам, существует определенная зависимость.
Для схемы с ОБ эта зависимость выражается соотношениями:
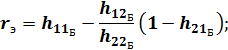
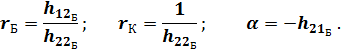
Система h-параметров называется гибридной (смешанной), так как одни h-параметры определяются в режиме х.х. на входе (I1=0), а другие в режиме к.з. на выходе (U2=0).
