Этот метод используется для построения начала таблицы. Формулы метода последовательных приближений:
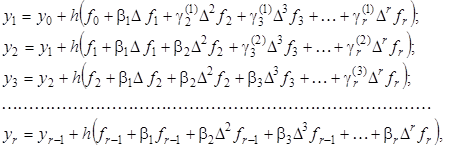
где b i – коэффициенты экстраполяционной формулы Адамса, r – порядок практически постоянных в пределах заданной точности разностей. Разностями r -го порядка пренебрегают.
Значения коэффициентов 
По этому методу сначала вычисляются приближённо значения y 1, y 2,¼, yr. Причём y 1 находят по первой формуле, оставляя в ней лишь два слагаемых; y 2 находят по второй формуле, ограничиваясь тремя слагаемыми, и т.д. Далее проводится итерационный процесс до тех пор, пока в пределах заданной точности не совпадут y 1, y 2,¼, yr, полученные на последнем и предпоследнем этапах. Значения y 1, y 2,¼, yr, полученные на последнем этапе, принимаются за окончательный результат.
Задание № 7
Решить численно одним из методов с точностью 10-5 на промежутке [0, 1] дифференциальное уравнение при начальном условии х (0) = 0.
Составить программу решения уравнения (допускается любой язык программирования), привести результаты её реализации и построить график решения. Проверить правильность решения, используя специализированные математические пакеты.
Вариант А
| Вариант | Уравнение | а | k |
| x ' = cos(at + x) + k (t – x) | 1.00 | 0.50 | |
| -"- | 1.25 | 0.75 | |
| -"- | 1.50 | 1.00 | |
| -"- | 1.75 | 1.25 | |
| -"- | 2.00 | 1.50 | |
x ' = 1 – sin(at + x) + 
| 1.00 | - 0.3 | |
| -"- | 1.25 | - 0.1 | |
| -"- | 1.50 | 0.1 | |
| -"- | 1.75 | 0.3 | |
| -"- | 2.00 | 0.5 | |
x ' =  + k x 2
| 1.00 | - 0.5 | |
| -"- | 1.25 | - 0.3 | |
| -"- | 1.50 | - 0.1 | |
| -"- | 1.75 | 0.1 | |
| -"- | 2.00 | 0.3 | |
| x ' = 1 + (a – t)sin(x) – (k + t) x | 0.50 | 1.00 | |
| -"- | 0.75 | 1.25 | |
| -"- | 1.00 | 1.50 | |
| -"- | 1.25 | 1.75 | |
| -"- | 1.50 | 2.00 | |
| x ' = (a – x 2)cos(t) + k x | 0.6 | 0.2 | |
| -"- | 0.7 | 0.3 | |
| -"- | 0.8 | 0.4 | |
| -"- | 0.9 | 0.5 | |
| -"- | 1.0 | 0.6 |
Вариант Б
| Вариант | Уравнение | a | k |
| x ' = 1 + a x sin(t) – k x 2 | 0.2 | 1.00 | |
| -"- | 0.4 | 1.25 | |
| -"- | 0.6 | 1.50 | |
| -"- | 0.8 | 1.75 | |
| -"- | 1.0 | 2.00 | |
| x ' = a e – (a + t x) + k (t 2 + x) | 0.2 | 0.3 | |
| -"- | 0.4 | 0.4 | |
| -"- | 0.6 | 0.5 | |
| -"- | 0.8 | 0.6 | |
| -"- | 1.0 | 0.7 | |
x ' = 
| 0.1 | 0.1 | |
| -"- | 0.2 | 0.2 | |
| -"- | 0.3 | 0.3 | |
| -"- | 0.4 | 0.4 | |
| -"- | 0.5 | 0.5 | |
x ' = 0.2 ch(a t + x) +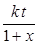 
| 0.3 | 1.00 | |
| -"- | 0.4 | 1.25 | |
| -"- | 0.5 | 1.50 | |
| -"- | 0.6 | 1.75 | |
| -"- | 0.7 | 2.00 | |
| - 0.5 | 0.2 | |
| -"- | - 0.4 | 0.3 | |
| -"- | - 0.3 | 0.4 | |
| -"- | - 0.2 | 0.5 | |
| -"- | - 0.1 | 0.6 |
Замечание 1. В рамках пакета Maple проверка правильности решения задачи осуществляется следующим образом:
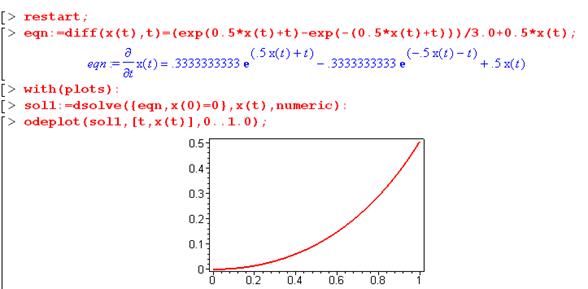
Таблица значений решения в узлах сетки с шагом h = 0.05 приведена ниже.
Замечание 2. В рамках пакета Mathcad решение обыкновенных дифференциальных уравнений осуществляется последовательностью специальных команд.
Сначала формируются "матрицы" (в данном случае скаляры) начальных 
условий и правой части. Затем командой rkfixed (или какой-либо другой) осуществляется сама процедура решения.
0 0
0.05000000000000 0.00084520959923
0.10000000000000 0.00343083039397
0.15000000000000 0.00783786372686
0.20000000000000 0.01415598922061
0.25000000000000 0.02248458081565
0.30000000000000 0.03293379527424
0.35000000000000 0.04562590720360
0.40000000000000 0.06069676562373
0.45000000000000 0.07829758606469
0.50000000000000 0.09859694045094
0.55000000000000 0.12178321860328
0.60000000000000 0.14806740950846
0.65000000000000 0.17768656848628
0.70000000000000 0.21090780566410
0.75000000000000 0.24803330959979
0.80000000000000 0.28940623751877
0.85000000000000 0.33541823340112
0.90000000000000 0.38651842970525
0.95000000000000 0.44322513172968
1.00000000000000 0.50614014425799
MATLAB
Maple Mathcad
Таблица значений функции приведена выше.
Замечание 3. Пакет MATLAB требует оформления правой части уравнения в виде m-функции:
function df=DifEq(t,x)
global a k
df=(exp(k*x+t)-exp(-(k*x+t)))/(2.0*(0.9+a))+k*x;
Затем вводятся команды:
Таблица значений функции приведена выше. Ниже представлен график решения.
