Краткая теория
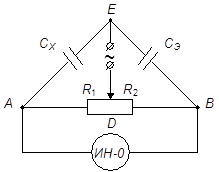Рис.1.
|
Для определения ёмкости конденсаторов можно воспользоваться мостовой схемой (рис.1). На схеме: Сэ - конденсатор известной емкости, Сx - исследуемый конденсатор, ИН-0 - индикатор нуля (вольтметр переменного тока или электронный осциллограф).
Напряжение со звукового генератора подводится к одной диагонали моста (DE), а в другую диагональ моста (AB) включается индикатор нуля. Принцип измерения основан на нахождении такого положения движка реостата, при котором потенциалы точек А и В одинаковы (j А = j В), ток в индикаторе нуля отсутствует, а мост находится в равновесии.
Выведем условие электрического равновесия моста. Рассмотрим электрическую ветвь моста DAE. Найдем заряд dq, прошедший по этой ветви за время dt:
,
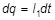где ток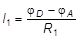 
.
Из определения ёмкости конденсатора следует, что
dq = Cx (j A - j E).
Тогда получим:
.
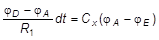Аналогичное выражение имеет место для ветви DBE:
.
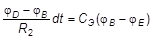Из последних двух формул, учитывая, что j A = j B, можно записать:
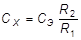. (1)
Порядок выполнения
1. Собрать установку по схеме рис.1.
2. В качестве реохорда использовать реостат на 500 Ом (Сопротивление реостата указано ориентировочно). Эталонный конденсатор имеет емкость 0,25 мкФ..
3. Подать на схему напряжение со звукового генератора (U» 10 В, f» 1 кГц) и, передвигая движок реостата, добиться наличия одинаковых потенциалов в точках А и В, т.е. добиться равновесия моста. При равновесии моста на экране электронного осциллографа наблюдается минимальный по амплитуде сигнал.
4. Отключив предварительно реостат от установки, с помощью мультиметра (в режиме омметра) измерить сопротивления R1 и R2 и, по формуле (1), определить ёмкость двух конденсаторов с неизвестной ёмкостью.
5. Определить результирующую ёмкость этих же двух конденсаторов при их параллельном и последовательном соединении.
6. По известным формулам вычислить электроёмкость последовательного и параллельного соединения неизвестных конденсаторов и сравнить и расчеты с экспериментальными данными.
7. Оценить погрешность измерения.
8. Результаты работы оформить в виде таблицы.
Упражнение 2. Определение емкости конденсатора методом куметра
Краткая теория
Метод куметра основан на том, что измеряемая ёмкость входит в состав колебательного контура с малым затуханием (с большой добротностью Q). Собственная частота колебательного контура, как это следует из теории свободных колебаний, определяется выражением:
,
где w02 =1/ LC, а b= R /2 L - коэффициент затухания.
Подставив значения w0 и b, получим:
.
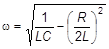Если контур обладает малым затуханием (сопротивление R очень мало), то вторым членом в выражении под радикалом можно пренебречь и записать:
.
Освобождаясь от радикала, получим:
,
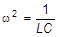откуда следует:
.
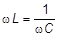Таким образом, собственная частота колебаний контура с малым затуханием определяется из равенства индуктивного и ёмкостного сопротивлений. Если резонанс в контуре достигнут, то для нахождения Сx достаточно знать величины w и L. Резонанса добиться можно, изменяя либо L, либо w.
 Рис.2.
|
Существует, однако, более простой способ достижения резонанса путем включения параллельно измеряемому конденсатору Сx градуированного конденсатора Сэ переменной ёмкости (рис.2).
Вначале ёмкость Сx отключена. Изменяя ёмкость эталонного конденсатора до значения Сэ = С 1, добиваются резонанса, который можно зафиксировать по максимальному показанию вольтметра V. Для этого случая будет справедливо соотношение:
.
Затем подключают измеряемый конденсатор Сx и вновь добиваются резонанса при значении Сэ = С 2. Для данного случая будет справедливо соотношение:
.
Из последних двух уравнений получаем:
Сx = С 1 - С 2.
Если градуированного конденсатора переменной ёмкости нет в распоряжении, то резонанса добиваются путем изменения частоты. Опыт производится в такой последовательности. Вначале ёмкость Сx отключена. Устанавливают эталонную ёмкость определенной величины Сэ = С = const и путем изменения частоты добиваются резонанса:
.
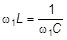Затем подключают измеряемый конденсатор Сx и вновь добиваются резонанса при той же ёмкости эталонного конденсатора:
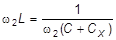
Из последних двух уравнений получаем:
.
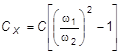Данное упражнение следует провести по второму варианту.
Порядок выполнения
1. Подготовить измерительную схему в соответствии с рис.2. Эталонную ёмкость следует взять величиной 1000 пФ. В качестве вольтметра использовать осциллограф.
2. Рассчитать (и установить на звуковом генераторе) резонансную частоту контура, пользуясь соотношением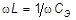 
. Эталонная электроёмкость рассчитывается по следующей формуле: Сэ = (1000 пФ + С 0) = 1130 пФ, где С 0 = 130 пФ – ёмкость монтажа эталонного конденсатора. Значение индуктивности L указано на катушке.
3. Подать со звукового генератора напряжение (не более 10 В) на контур с эталонным конденсатором, уточнить частоту резонанса.
4. Подключив конденсатор с неизвестной ёмкостью, определить её значение, добиваясь резонанса изменением частоты генератора.
5. Оценить погрешность измерения.
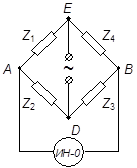Рис.3.
|
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Пользуясь схемой, изображённой на рис.3, выведите условие равновесия моста переменного тока в комплексной форме Z 1 Z 3 = Z 2 Z 4, где Zk = (Rk + iXk) – сопротивление (импеданс) одного из плеч моста.
2. Подставляя, в соответствии с реальной схемой (рис.1), в выражение Z 1 Z 3 = Z 2 Z 4 вместо сопротивлений Zk их значения, выраженные через Rk и Хk, и приравнивая их действительные и мнимые части, найдите два уравнения, которые являются условиями равновесия моста переменного тока. Пользуясь этими уравнениями, найдите условие равновесия мостика Сотти.
3. В чем заключается физическая основа применения метода куметра для измерения электроёмкости конденсаторов?
4. Какой тип резонанса (токов или напряжений) возникает в использованном колебательном контуре?
5. Чем ограничивается диапазон измерений ёмкостей в рассмотренных методах?
Лабораторная работа №8
Измерение мощности переменного тока и сдвига фаз между током и напряжением
Цель работы: измерение мощности переменного тока и сдвига фаз между током и напряжением для различных нагрузок с помощью ваттметра.
Приборы и принадлежности: источник питания, ваттметр, реостат, набор сопротивлений нагрузки.
КРАТКАЯ ТЕОРИЯ
