Рис. 3.9 Рис. 3.10
Таким образом, термодинамический цикл Отто состоит из двух изохор и двух адиабат (рис. 3.9). Площадь, ограниченная контурами цикла, представляет собой величину полезной работы цикла. В диаграмме T, s этот цикл имеет вид, показанный на рис. 3.10.
Термический КПД цикла с подводом тепла при v = const определяется из общего для всех циклов выражения  , если в него подставить значения отведенного в процессе 4 – 1 тепла q2 = cv(T4 – T1) и подведенного в изохорном процессе 2 – 3 тепла q1 = cv(T3 – T2):
, если в него подставить значения отведенного в процессе 4 – 1 тепла q2 = cv(T4 – T1) и подведенного в изохорном процессе 2 – 3 тепла q1 = cv(T3 – T2):
 . (3.17)
. (3.17)
Считая сv = const, преобразуем выражение (3.17) к виду:
 . (3.18)
. (3.18)
Из адиабаты 1 – 2 имеем:
 , (3.19)
, (3.19)
а из адиабаты 3 – 4:
 . (3.20)
. (3.20)
Правые части выражений (3.19) и (3.20) равны, поэтому T1 / T2 = T4 / T3,
 . (3.21)
. (3.21)
Подставляя соотношение (3.21) в формулу (3.18), получаем
 , (3.22)
, (3.22)
или, с учетом выражения (3.18) (зная, что v1 / v2 = ε):
 . (3.23)
. (3.23)
Из формулы (3.23) видно, что термический КПД цикла ДВС с подводом тепла при постоянном объеме зависит только от степени сжатия ε, с увеличением которой ht возрастает.
 Существенного повышения ε добиваются в двигателях высокого сжатия, в которых сжимается не горючая смесь, а чистый воздух. Температура конца процесса сжатия должна превышать температуру воспламенения топлива, впрыскиваемого в камеру сгорания, так как двигатель работает без постороннего источника зажигания, за счет самовоспламенения паров топлива. Степень сжатия ε при этом у современных двигателей достигает 12 – 20.
Существенного повышения ε добиваются в двигателях высокого сжатия, в которых сжимается не горючая смесь, а чистый воздух. Температура конца процесса сжатия должна превышать температуру воспламенения топлива, впрыскиваемого в камеру сгорания, так как двигатель работает без постороннего источника зажигания, за счет самовоспламенения паров топлива. Степень сжатия ε при этом у современных двигателей достигает 12 – 20.
По имени немецкого инженера Р. Дизеля, построившего в 1897 г. двигатель, работающий по этому принципу, двигатели внутреннего сгорания высокого сжатия иногда называются дизелями.
В первых дизелях с целью улучшения распыливания топлива использовался сжатый воздух. Привод компрессора осуществлялся от вала двигателя, расходуя значительную часть его мощности. Применение форсунок с воздушным распыливанием позволяет так отрегулировать процесс горения при одновременном увеличении камеры сгорания, что он протекает практически при постоянном давлении: р = const. В остальном цикл Дизеля (рис. 3.11) аналогичен рассмотренному ранее циклу Отто.
Термический КПД цикла с изобарным подводом тепла
 . (3.24)
. (3.24)
В изобарном процессе подвода тепла 2 – 3 происходит некоторое увеличение объема до начала адиабатного процесса расширения 3 – 4, поэтому для характеристики цикла Дизеля вводится показатель – степень предварительного расширения
 . (3.25)
. (3.25)
Отношение температур T4 / T1 также можно выразить через ρ, воспользовавшись уравнениями 4 – 3 и 1 – 2:
 ;
;  .
.
Так как v4 = v1, то
 . (3.26)
. (3.26)
После подстановки связей (3.19), (3.25) и (3.26) в уравнение (3.24) окончательно получаем:
 . (3.27)
. (3.27)
Термический КПД с ростом ε, как и в цикле Отто, увеличивается, а с ростом ρ, что соответствует увеличению нагрузки на двигатель, падает.
К 1904 г. относят изобретение двигателя Тринклера, который запатентовал форсунку, способную распыливать топливо без помощи сжатого воздуха. Плунжерным насосом создается высокое давление топлива (до 150 – 200 МПа), за счет чего осуществляется механическое его распыливание при впрыске в камеру сгорания. Горение топлива при этом происходит в две стадии.
 Вследствие периода задержки воспламенения топлива происходит его накопление и испарение. Образовавшаяся горючая смесь после самовоспламенения сгорает почти мгновенно. Эта стадия горения соответствует изохорному участку 2 – z подвода тепла q1v в термодинамическом цикле двигателя Тринклера (рис. 3.12). Сгорание остальной части топлива происходит постепенно по мере поступления его из форсунки. На диаграмме p, v это отражается изобарным участком подвода тепла q1p в процессе z – 3.
Вследствие периода задержки воспламенения топлива происходит его накопление и испарение. Образовавшаяся горючая смесь после самовоспламенения сгорает почти мгновенно. Эта стадия горения соответствует изохорному участку 2 – z подвода тепла q1v в термодинамическом цикле двигателя Тринклера (рис. 3.12). Сгорание остальной части топлива происходит постепенно по мере поступления его из форсунки. На диаграмме p, v это отражается изобарным участком подвода тепла q1p в процессе z – 3.
Такой характер горения топлива свойственен большинству современных бескомпрессорных дизелей.
Термический КПД цикла со смешанным подводом тепла
 (3.28)
(3.28)
Выразим отношение температур в уравнении (3.28) через характеристики ДВС e, λ, ρ.
Для изохоры 4 – 1, используя уравнения адиабат 4 – 3 и 1 – 2:  ;
;  , имеем:
, имеем:
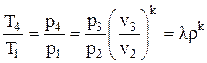 , (3.29)
, (3.29)
где λ = р3 / р2 – степень повышения давления в процессе изоxoрного подвода тепла. Для изохоры 2 – z
 . (3.30)
. (3.30)
Поскольку T3 / Tz = v3 / vz = ρ, то
 . (3.31)
. (3.31)
Подставив в уравнение (3.28) вместо отношений температур их значения, получаем
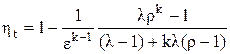 . (3.32)
. (3.32)
Формула термического КПД смешанного цикла имеет в известной мере обобщающее значение, так как из нее могут быть получены выражения ηt циклов Отто и Дизеля. Действительно, в цикле Отто отсутствует изобарный участок подвода тепла, а все тепло подводится при v = const. Это условие выдерживается, если в смешанном цикле положить r = 1. Тогда формула (3.32) трансформируется в (3.23). В цикле Дизеля нет изохорного участка, т. е. λ = 1. Подставляя это условие в уравнение (3.32), получим формулу (3.27) термического КПД цикла с подводом тепла при р = const.
 Для решения вопроса о целесообразности использования того или иного цикла ДВС проведем их термодинамическое сравнение в Т, s-диаграмме (рис. 3.13). Будем считать, что отведенное тепло q2 во всех случаях одинаково. Степень сжатия e в смешанном Цикле и в цикле Дизеля существенно выше, чем в цикле с изохорным подводом тепла. Поэтому точка 2v расположится на адиабате сжатия много ниже, чем точка 2p и 2см (которые можно совместить, так как e в циклах Дизеля и Тринклера примерно одинаковы). Точки конца процесса подвода тепла 3v, 3р, 3см получаются из построения процессов
Для решения вопроса о целесообразности использования того или иного цикла ДВС проведем их термодинамическое сравнение в Т, s-диаграмме (рис. 3.13). Будем считать, что отведенное тепло q2 во всех случаях одинаково. Степень сжатия e в смешанном Цикле и в цикле Дизеля существенно выше, чем в цикле с изохорным подводом тепла. Поэтому точка 2v расположится на адиабате сжатия много ниже, чем точка 2p и 2см (которые можно совместить, так как e в циклах Дизеля и Тринклера примерно одинаковы). Точки конца процесса подвода тепла 3v, 3р, 3см получаются из построения процессов
v = const, p = const и смешанного.
При равных значениях q2 величина термического КПД ηt = 1 – q2 / q1 будет определяться значением q1. Как видно из диаграммы (см. рис. 3.13),
q1см > q1p > q1v, поэтому ηt см > ηt p > ηt v.
Сравнение циклов показывает, что термический КПД бескомпрессорных дизелей имеет наибольшее значение, поэтому они широко применяются в качестве стационарных и судовых установок, а также в тяжелых транспортных средствах – тепловозах, самосвалах. Двигатели же низкого сжатия, в частности бензиновые карбюраторные ДВС, работают с наименьшим КПД. Тем не менее они имеют большое распространение (в силу малого веса) в автомобильном транспорте и в других случаях, когда бывает необходимость в легком
двигателе.
Что касается компрессорных дизелей, работающих по циклу с подводом тепла при р = const, то в настоящее время они не применяются, так как имеют низкий эффективный КПД из-за больших потерь мощности на привод компрессора для сжатия воздуха.






