Кратко рассмотрим основные термодинамические процессы идеального газа, закономерности которых понадобятся в дальнейшем, в частности, при рассмотрении циклов двигателей.
Изохорный процесс. При изохорном процессе выполняется условие dv = 0 или v = const. Из уравнения состояния идеального газа следует, что 
, т.е. давление газа прямо пропорционально его абсолютной температуре:
. (4.1)
На рис. 4.1. представлен график процесса.
| Рис. 4.1. Изображение изохорного процесса в p, v – (а) и T, s – (б) координатах |
Работа расширения в этом процессе равна нулю, так как dv = 0.
Количество теплоты, подведенной к рабочему телу в процессе 12
.
Так как l = 0, то в соответствии с первым законом термодинамики 
и
. (4.2)
Поскольку внутренняя энергия идеального газа является функцией только его температуры, то формула (4.2) справедлива для любого термодинамического процесса идеального газа.
Изменение энтропии в изохорном процессе определяется из формулы (3.4) при v 1 = v 2, поскольку 
:
, откуда 
, (4.3)
т.е. зависимость Т от s (в T-s диаграмме) является экспоненциальной (см. рис. 4.1).
Изобарный процесс. Из уравнения состояния идеального газа при р = const находим 
, или
, (4.4)
т.е. в изобарном процессе объем газа пропорционален его абсолютной температуре (закон Гей-Люссака, 1820 г.). На рис. 4.2 изображены графики процесса в p, v- и T, s- диаграммах.
| Рис. 4.2. Изображение изобарного процесса в p, v - и T, s - координатах |
Из выражения (2.6) следует, что
. (4.5)
Так как 
и 
, то одновременно
. (4.6)
Количество теплоты, сообщаемой газу при нагревании (или отдаваемой им при охлаждении), находим из уравнения (2.24)
. (4.7)
Из уравнения (2.28)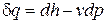 
при р = const получим
или 
,
т.е. количество теплоты, подведенной в изобарном процессе к закрытой системе, равно разности ее энтальпий. Сравнивая выражение первого закона термодинамики, определенное через энтальпию для изобарного процесса, с формулой (4.7), получим выражение для подсчета энтальпии
.
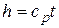Формулу для изменения энтропии в изобарном процессе получим, подставив в уравнение 
отношение 
вместо 
(из уравнения (4.4)) и с р вместо cv + R из уравнения (2.20):
или 
. (4.8)
В T,s - диаграмме изобара тоже является экспонентой, как и изохора, но поскольку cp > cv, она положе.
Изотермический процесс. При изотермическом процессе температура постоянна, следовательно, 
, или
, (4.9)
т.е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – падает (закон Бойля – Мариотта, 1662 г.).
Графиком изотермического процесса в p, v - координатах, как показывает уравнение (4.9) является равнобокая гипербола, для которой координатные оси служат асимптотами (рис. 4.3).
Поскольку температура не меняется, то внутренняя энергия идеального газа в данном процессе остается постоянной (D u = 0) и вся подводимая к газу теплота полностью превращается в работу расширения:
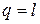. (4.10)
| Рис. 4.3. Изображение изотермического процесса в p, v - и T, s - координатах |
При изотермическом сжатии от газа отводится теплота в количестве, равном затраченной на сжатие работе.
Адиабатный процесс. Процесс, происходящий без теплообмена с окружающей средой (d q = 0), называется адиабатным. Для того чтобы осуществить такой процесс, следует либо теплоизолировать газ, т.е. поместить его в адиабатную оболочку, либо провести процесс настолько быстро, чтобы изменение температуры газа, обусловленное его теплообменом с окружающей средой, было пренебрежимо мало по сравнению с изменением температуры, вызванным расширением или сжатием газа.
Уравнение первого закона термодинамики для адиабатного процесса в закрытой системе можно записать в виде
и 
. (4.11)
Имея в виду, что 
, а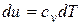 
, и поделив с учетом этого первое из уравнений (4.11) на второе, получим,
или 
.
Интегрируя последнее уравнение при условии, что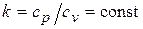 
, находим
и 
.
После потенцирования имеем 
, или
. (4.12)
Это и есть уравнение адиабаты идеального газа при постоянном отношении теплоемкостей (k = const).
Величина
(4.13)
называется показателем адиабаты. Для одноатомного газа k = 1,66, для двухатомного k = 1,4, для трех- и многоатомных газов k = 1,33.
Поскольку k > 1, то в координатах p, v (рис. 4.4) линия адиабаты идет круче линии изотермы: при адиабатном расширении давление понижается быстрее, чем при изотермическом, так как в процессе расширения уменьшается температура газа.
| Рис. 4.4. Изображение адиабатного процесса в p, v - и T, s - координатах |
Записав из уравнения Клапейрона, написанного для состояний 1 и 2, отношение температуры через отношение давлений и заменив в нем отношение давлений через отношение объемов из уравнения (4.12) или наоборот, получим уравнение адиабатного процесса в форме, выражающей зависимость температуры от объема или давления:
; 
. (4.14)
Работа расширения в адиабатном процессе согласно первому закону термодинамики совершается за счет уменьшения внутренней энергии и может быть вычислена по формуле
.
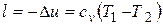Из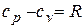 
имеем 
. Подставив отсюда cv в предыдущее соотношение, получим
. (4.15)
В данном процессе теплообмен газа с окружающей средой исключается, поэтому q = 0. Выражение 
показывает, что теплоемкость адиабатного процесса равна нулю.
Поскольку при адиабатном процессе d q = 0, энтропия рабочего тела не изменяется (ds = 0 и s = const). Следовательно, на Т, s - диаграмме равновесный адиабатный процесс изображается вертикальной прямой линией.
Политропный процесс и его обобщающее значение. Любой произвольный процесс можно описать в p, v - координатах (по крайней мере, на небольшом участке) уравнением
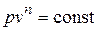, (4.16)
подбирая соответствующее значение n. Процесс, описываемый уравнением (4.16), называется политропным. Показатель политропы n может принимать любое численное значение в пределах от -¥ до +¥, но для данного процесса он является величиной постоянной.
Связь между параметрами в политропном процессе выражается теми же формулами, что и в адиабатном процессе с заменой показателя адиабаты k на показатель политропы n. Работа в политропном процессе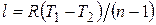 
.
Смеси идеальных газов
Все зависимости, полученные выше для идеальных газов, справедливы и для их смесей, если в них подставлять газовую постоянную, молекулярную массу и теплоемкость смеси.
Закон Дальтона. В инженерной практике часто приходится иметь дело с газообразными веществами, близкими по свойствам к идеальным газам и представляющими собой механическую смесь отдельных компонентов различных газов, химически не реагирующих между собой. Это так называемые газовые смеси. В качестве примера можно назвать продукты сгорания топлива в двигателях внутреннего сгорания, топках печей и паровых котлов, влажный воздух в сушильных установках и т.д.
Основным законом, определяющим поведение газовой смеси, является закон Дальтона: полное давление смеси идеальных газов равно сумме парциальных давлений всех входящих в нее компонентов:
. (4.17)
Парциальное давление pi – давление, которое имел бы газ, если бы он один при той же температуре занимал весь объем, занимаемый смесью.
Способы задания смеси. Состав смеси может быть задан массовыми, объемными или мольными долями.
Массовой долей называется отношение массы отдельного компонента Мi к массе смеси М:
. (4.18)
Очевидно, что 
и 
.
Массовые доли часто задаются в процентах. Например, для сухого воздуха 
77 %; 
23 %.
Объемная доля представляет собой отношение приведенного объема газа Vi к полному объему смеси V:
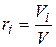. (4.19)
Приведенным называется объем, который занимал бы данный газ, если бы его давление и температура равнялись давлению и температуре смеси.
Для вычисления приведенного объема Vi запишем два уравнения состояния для i -го компонента:
; (4.20)
. (4.21)
Первое уравнение относится к состоянию компонента газа в смеси, когда он имеет парциальное давление pi и занимает полный объем смеси, а второе уравнение – к приведенному состоянию, когда давление и температура компонента равны, как и для смеси, р и Т. Из уравнений следует, что
. (4.22)
Просуммировав соотношения (4.22) для всех компонентов смеси, с учетом закона Дальтона 
получим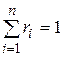 
. Объемные доли также часто задаются в процентах. Для воздуха 
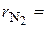79 %, 
21 %.
Иногда бывает удобнее задать состав смеси мольными долями. Мольной долей называется отношение количества молей Ni рассматриваемого компонента к общему количеству молей смеси N.
Пусть газовая смесь состоит из N 1 молей первого компонента, N 2 молей второго компонента и т.д. Число молей смеси 
, а мольная доля компонента будет равна 
.
В соответствии с законом Авогадро объемы моля любого газа при одинаковых р и Т, в идеально газовом состоянии одинаковы. Поэтому приведенный объем любого компонента может быть вычислен как произведение объема моля V m на число молей этого компонента, т.е.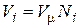 
, а объем смеси – по формуле 
. Тогда 
и, следовательно, задание смеси идеальных газов мольными долями равнозначно заданию ее объемными долями.
Газовая постоянная смеси газов. Просуммировав левые и правые части уравнения (4.20) для всех компонентов смеси и имея в виду, что 
, получим 
. Учитывая, что 
(4.17), можно записать
, (4.23)
где
. (4.24)
Из уравнения (4.23) следует, что смесь идеальных газов также подчиняется уравнению Клапейрона.
Поскольку в соответствии с (1.6)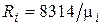 
, то из (4.24) следует, что газовая постоянная смеси [Дж/(кг×К)] равна
, (4.25)
где m i выражена в кг/кмоль.
Кажущаяся молекулярная масса смеси. Выразим формально газовую постоянную смеси по формуле (1.6), введя кажущуюся молекулярную массу смеси mсм:
. (4.26)
Сравнивая правые части соотношений (4.25) и (4.26), найдем
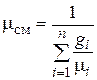. (4.27)
Из определения массовых долей следует, что
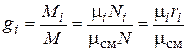. (4.28)
Просуммировав это соотношение для всех компонентов и учитывая, что , получим выражение для кажущейся молекулярной массы смеси, заданной объемными долями:
. (4.29)
Соотношение между объемными и массовыми долями. Подставив (4.29) в (4.28), получаем
. (4.30)
Поскольку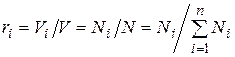 
, то
.
Разделив числитель и знаменатель этой формулы на массу смеси М, получим
. (4.31)
Теплоемкость смеси идеальных газов. Если смесь газов задана массовыми долями, то ее массовая теплоемкость с определяется как сумма произведений массовых долей на массовую теплоемкость каждого компонента, т. е.
; 
. (4.32)
При задании смеси объемными долями объемная теплоемкость смеси
; 
. (4.33)
Аналогично мольная теплоемкость смеси равна произведению объемных долей на мольные теплоемкости составляющих смесь газов:
; 
. (4.34)
