Моделирование непрерывной случайной величины. Метод обратной функции

Учебное пособие

по дисциплине «Моделирование»

СОДЕРЖАНИЕ

 

1. Основные определения и понятия теории моделирования, области использования 3

2. Основные методы моделирования. 7

3. Классификация видов моделирования. 8

4. Математические модели систем. 10

5. Основные подходы к построению моделей системы.. 11

6. Введение в имитационное моделирование систем. 13

6.1. Проблемы применения имитационного моделирования. 13

6.2. Принцип Dt и особых состояний dz. 15

6.3. Пример использования принципа при моделировании системы.. 16

6.4. Пример использования принципа особых состояний при моделировании системы.. 19

7. Математические основы имитационного моделирования. 22

7.1. Методы генерации случайных чисел. 22

7.2. Методы имитационного моделирования случайных величин. 25

7.3. Имитационное моделирование случайных событий. 28

8. Статистическое моделирование. 32

8.1. Метод статистического моделирования. 32

8.2. Обработка результатов моделирования. 35

9. Элементы теории Марковских случайных процессов, используемые при моделировании систем. 37

9.1. Потоки событий. 37

9.2. Марковский случайный процесс. 41

9.3. Марковский случайный процесс «гибели и размножения». 45

10. Элементы теории массового обслуживания, применяемые при моделировании систем 46

10.1. Основные определения и понятия. Структура СМО. Классификация СМО.. 46

10.2. Системы массового обслуживания, в которых протекает Марковский случайный процесс «гибели и размножения». 51

10.2.1. Основные типы систем, соответствующие процессу «гибели и размножения». 51

10.2.2. Расчет характеристик СМО на основе использования аналитического метода. 52

11. Инструментальные средства моделирования. 56

11.1. Классы инструментальных средств. 56

11.2. Технология разработки имитационной модели. 57

11.3. Моделирование работы вычислительной системы в среде GPSS/World. 57

11.4. Моделирование значений случайной величины с заданным законом распределения и обработка результатов моделирования средствами GPSS/World. 67

11.5. Основные направления развития инструментальных средств моделирования. 74

Список литературы.. 74

 

1. Основные определения и понятия теории моделирования, области использования

С точки зрения философии, моделирование представляет собой один из методов познания мира.

С практической точки зрения моделирование – метод исследования, основанный на замене исследуемого объекта-оригинала его моделью и на работе с ней (вместо объекта).

Соответственно теория моделирования – теория замещения объекта-оригинала его моделью и исследования свойств объекта на его модели. Базовые понятия теории моделирования: моделирование, модель, система.

Модель (объекта - оригинала) (от лат. Modus – «мера», «объем», «образ»)– вспомогательный объект, отражающий наиболее существенные для исследования закономерности, суть, свойства, особенности строения и функционирования объекта-оригинала.

Когда говорят о моделировании, обычно имеют в виду моделирование некоторой системы.

Система – совокупность взаимосвязанных элементов, объединенных для реализации общей цели, обособленная от окружающей среды и взаимодействующая с ней как целое и проявляющая при этом основные системные свойства.

Приведем основные свойства системы.

Свойство эмергентности или эмерджентности. Результат поведения системы дает эффект отличный от «сложения» (независимого соединения) любым способом результатов поведения всех, входящих в систему элементов. Свойства системы не сводятся к совокупности свойств частей, из которых она состоит, и не выводятся из них.

Свойство цельности, целевости. Система рассматривается как нечто целое, обособленное от окружающей среды.

Свойство структурированности. Система имеет части, целесообразно связанные между собой.

Свойство подчиненности цели. Вся организация системы подчинена некоторой цели.

Свойство эргатичности. Система может в качестве одной из частей включать человека. Пример – сложные системы управления, составной элемент контура управления – человек-оператор (или группа операторов): служба аэропорта, диспетчерская служба, система управления самолетом и т.п.

Свойство бесконечности. Невозможность полного познания системы и ее всестороннего представления любым конечным множеством моделей.

Свойство иерархичности. Система может иметь несколько качественно разных уровней строения. При декомпозиции системы каждая ее подсистема или часть может рассматриваться как целостная подсистема. Сама система является в свою очередь частью некоторой надсистемы – более широкой системы.

Примеры систем – система по обработке потоков заявок, библиотека, магазин, производственный участок, линия связи и т.д.

Сейчас нельзя назвать область человеческой деятельности, в которой в той или иной степени не использовались бы методы моделирования. Особенно это относится к сфере управления различными системами, где основными являются процессы принятия решений на основе получаемой информации. Методы моделирования широко применяются при исследовании, проектировании, внедрении АСУ.

Выбор метода моделирования и необходимая детализация проекта зависят от этапа разработки АСУ. На этапах обследования объекта управления (например, промышленного предприятия) и разработки ТЗ на проектирование АСУ модели носят описательный характер и преследуют цель наиболее полно представить в компактной форме информацию об объекте, необходимую разработчику системы.

На этапе разработки технического проекта АСУ моделирование служит для решения задачи проектирования, т.е. выбора оптимального по определенному критерию при заданных ограничениях варианта из множества допустимых (построение оптимизационных моделей).

На этапе внедрения и эксплуатации АСУ строятся модели для проигрывания возможных ситуации для принятия обоснованных и перспективных решений по управлению объектом. Моделирование (имитацию) также широко применяют при обучении и тренировке персонала АСУ. Моделирование носит характер деловых игр.

В настоящее время при анализе и синтезе больших систем получил развитие системный подход, который отличается от классического (индуктивного) подхода.

Рассмотрим особенности этих двух подходов.

Классический подход. Исторически первым сложился классический подход к изучению объекта, моделированию системы. Классический подход синтеза модели (М) системы представлен на рис. 1. Реальный объект, подлежащий моделированию, разбивается на подсистемы, выбираются исходные данные (Д) для моделирования и ставятся цели (Ц), отражающие отдельные стороны процесса моделирования. По отдельной совокупности исходных данных ставится цель моделирования отдельной стороны функционирования системы, на базе этой цели формируется некоторая компонента (К) будущей модели. Совокупность компонент объединяется в модель.

Т.о. происходит суммирование компонент, каждая компонента решает свои собственные задачи и изолирована от других частей модели. Применим подход только для простых систем, где можно не учитывать взаимосвязи между компонентами. Можно отметить две отличительные стороны классического подхода:

- наблюдается движение от частного к общему при создании модели;

- созданная модель (система) образуется путем суммирования отдельных ее компонент и не учитывает возникновение нового системного эффекта.

Рис. 1. Классический подход к изучению объекта, построению модели

Системный подход. Системный подход – методологическая концепция, основанная на стремлении построить целостную картину изучаемого объекта с учетом важных для решаемой задачи элементов объекта, связей между ними и внешних связей с другими объектами и окружающей средой. С усложнением объектов моделирования возникла необходимость их наблюдения с более высокого уровня. В этом случае разработчик рассматривает данную систему как некоторую подсистему более высокого ранга. Например, если ставится задача проектирования АСУ предприятия, то с позиции системного подхода нельзя забывать, что эта система является составной частью АСУ объединением. В основе системного подхода лежит рассмотрение системы как интегрированного целого, причем это рассмотрение при разработке начинается с главного – формулировки цели функционирования. На рис. 2. условно представлен процесс синтеза модели системы на основе системного подхода.

Рис. 2. Системный подход к изучению объекта, построению модели

На основе исходных данных (Д), полученных на основе анализа внешней среды, цели функционирования (Ц) формулируются требования (Т) к модели системы. На базе этих требований выделяются ориентировочно подсистемы (П), элементы (Э) и осуществляется наиболее сложный этап синтеза модели – выбор составляющих систем, для чего используются специальные критерии выбора (КВ). Системный подход предполагает последовательный переход от общего к частному, когда в основе рассмотрения лежит цель, причем исследуемый объект выделяется из окружающей среды.

Важным для системного подхода является определение структуры системы - совокупности связей между элементами системы, отражающих их взаимодействие. Существуют структурные и функциональные подходы к исследования структуры системы с ее свойствами. При структурном подходе выявляются состав выделенных элементов системы и связи между ними. При функциональном подходе рассматриваются алгоритмы поведения системы (функции - свойства, приводящие к достижению цели).

 

2. Основные методы моделирования

Развитие методы моделирования получили с развитием вычислительной техники. Исторически первыми были разработаны аналитические методы моделирования и сложился аналитический подход к исследованию систем.

Аналитические методы моделирования. Аналитические методы позволяют получить характеристики системы как некоторые функции параметров ее функционирования. Таким образом, аналитическая модель представляет собой систему уравнений, при решении которой получают параметры, необходимые для оценки системы (время ответа, пропускную способность и т.д.). Использование аналитических методов дает достаточно точную оценку, которая, зачастую, хорошо соответствует действительности. Смена состояний реальной системы происходит под воздействием множества как внешних, так и внутренних факторов, подавляющее большинство из которых носят стохастический характер. Вследствие этого, а также большой сложности большинства реальных систем, основным недостатком аналитических методов является то, что при выводе формул, на которых они основываются и которые используются для расчета интересующих параметров, необходимо принять определенные допущения. Тем не менее, нередко оказывается, что эти допущения вполне оправданы.

Численные методы моделирования – преобразование модели к уравнениям, решение которых возможно методами вычислительной математики. Класс задач значительно шире. Однако численные методы не дают точных решений, но позволяют задать точность решения.

Имитационные методы моделирования. С развитием вычислительной техники широкое применение получили имитационные методы моделирования для анализа систем, преобладающими в которых являются стохастические воздействия.

Суть ИМ заключается в имитации процесса функционирования системы во времени, соблюдением таких же соотношений длительности операций как в системе оригинале. При этом имитируются элементарные явления, составляющие процесс; сохраняется их логическая структура, последовательность протекания во времени. Результатом ИМ является получение оценок характеристик системы.

3. Классификация видов моделирования

 

В основу классификации моделирования можно положить различные признаки.

В зависимости отхарактера изучаемых процессов в системе все виды моделирования м.б. разделены на

- детерминированные и стохастические

Детерминированное моделирование применяется для исследования систем, поведение которых можно абсолютно точно предвидеть. Например, путь, пройденный автомобилем, при равноускоренном движении в идеальных условиях; устройство, возводящее в квадрат число на входе. Соответственно детерминированный процесс, детерминированная модель.

Стохастическое (теоретико-вероятностное) моделирование применяется для исследования систем, состояние которых зависит не только от контролируемых, но и от неконтролируемых воздействий или в ней самой есть источник случайности. Например, человек и все системы, которые включают человека. Приведем пример стохастических систем, это - заводы, аэропорты, сети и системы ЭВМ, магазины, предприятия бытового обслуживания и т.п.

- статическое и динамическое

Статистическое моделирование служит для описания систем в какой-либо момент времени.

Динамические моделирование отражает изменение системы во времени (выходные характеристики системы в данный момент времени определяются характером входных воздействий в прошлом и настоящем). Устройство, возводящее x(t) в квадрат. Примером динамических систем является биологические, экономические, социальные системы; такие искусственные системы как завод, предприятия, поточная линия и т.п.

- дискретное и непрерывное

Дискретное моделирование применяют для исследования систем, в которых входных и выходные характеристики измеряется или изменяется во времени дискретно, через dt (например, часы), в противном случае применяют непрерывное моделирование. Например: ЭВМ, электронные часы, электросчетчик - дискретные системы; песочные часы, солнечные часы, нагревательные приборы и т.д. - непрерывные системы.

В зависимости от формы представления объекта (системы) можно выделить мысленное и реальное моделирование.

При реальном (натурном) моделировании исследование характеристик системы проводится на реальном объекте, либо на его части. РМ является наиболее адекватным, но его возможности с учетом особенностей реальных объектов ограничены. Например, проведение реального моделирования с АСУ предприятия требует во-первых, создания АСУ; во-вторых, проведения экспериментов с предприятиями, что невозможно.

К реальному моделированию относят производственный эксперимент и комплексные испытания, которые обладают высокой степенью достоверности.

Другой вид реального моделирования – физическое. При физическом моделировании исследование проводится на установках, которые сохраняют природу явления и обладают физическим подобием.

Мысленное моделирование применяется для моделирования систем, которые практически не реализуемы на заданном интервале времени. В основе мысленного моделирования - создание идеальной модели основанной на идеальной, мыслительной аналогии. Различают два вида моделирования: образное (наглядное) и знаковое.

При образном моделировании на базе представлений человека о реальных объектах создаются различные наглядные модели, отображающие явления и процессы, протекающие в объекте (например, модели частиц газов в кинетической теории газов в виде упругих шаров, воздействующих друг на друга во время столкновения).

При знаковом моделировании описывают моделируемую систему с помощью условных знаков, символов, в частности, в виде математических, физических и химических формул.

Наиболее мощный и развитый класс знаковых моделей представляют математические модели.

Математическая модель – это искусственно созданный объект в виде математических, знаковых формул, который отображает и воспроизводит структуру, свойства, взаимосвязи и отношения между элементами исследуемого объекта. Именно этот класс моделей мы и будем рассматривать и далее говорить только о математическом моделировании.

Математическое моделирование (Губарев В.В.) – метод исследования, основанный на замене исследуемого объекта-оригинала его математической моделью и на работе с ней (вместо объекта).

Математическое моделирование можно разделить на аналитическое, имитационное, комбинированное.

При АМ создается аналитическая модель объекта в виде алгебраических, дифференциальных, конечно-разностных уравнений. Аналитическая модель исследуется либо аналитическими методами, либо численными методами.

При имитационном моделировании создается Имитационная модель, используется метод статистического моделирования для реализации Имитационной модели на ЭВМ.

Комбинированное моделирование – декомпозиция процесса функционирования системы на подпроцессы. Для тех из них, где это возможно, используют аналитические методы, в противном случае – имитационные.

 

4. Математические модели систем

Важным этапом моделирования является создание математической модели исследуемой системы. На базе математической модели происходит анализ характеристик системы, при компьютерном моделирования на основе математической модели создается алгоритм программ для получения информации о поведении системы. Формальное описание объекта исследование необходимо также для взаимопонимания между специалистами разных областей, объединенных для решения какой-либо глобальной задачи.

В общем случае математическую модель любой динамической системы можно представить в следующем виде:

,

где - совокупность входных воздействий на систему,

- совокупность внутренних параметров системы,

- совокупность выходных характеристик системы,

F - закон функционирования системы.

Процесс функционирования системы можно рассматривать как последовательную смену состояний :

,

где - совокупность начальных состояний.

Таким образом, общую математическую модель системы можно также представить следующим образом:

.

 

5. Основные подходы к построению моделей системы

При построении математических моделей процессов функционирования систем можно выделить следующие основные подходы: непрерывно-детерминированный, дискретно-детерминированный, дискретно-стохастический, непрерывно-стохастический. Соответственно этим подходам были разработаны типовые математические схемы создания моделей.

1. Непрерывно-детерминированный подход использует в качестве математических моделей системы дифференциальных уравнений. Например, процесс малых колебаний маятника описывается обыкновенным дифференциальным уравнением:

,

где m, l - масса и длина подвеса маятникаl; g - ускорение свободного падения; 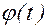- угол отклонения маятника в момент времени t. Из этого уравнения свободного колебания маятника можно найти оценки интересующих характеристик. Созданные на основе этого подхода математические модели исследуются, как правило, аналитическими способами. Возможным приложением данный подход является анализ систем автоматического управления непрерывными процессами, например, система управления температурой печи.

Простейшую систему автоматического управления можно представить в следующем виде (рис. 3):

 

x(t) h'(t) y(t)

 

Рис. 3.

 

Разность между заданными y_зад(t) и действительным y(t) законами изменения управляемой величины есть ошибка управления h'(t)=y_зад(t)-y(t). Если предписанный закон изменния управляемой величины соответствует закону изменения входного (задающего) воздействия, т.е. x(t)=y(t), то h'(t)=x(t)-y(t).Принцип обратной связи (основной принцип систем автоматического управления): приведение в соответствие выходной переменной y(t) ее заданному значению используется информация об отклонении h'(t) между ними. Задачей системы автоматического управления является изменение выходных сигналов согласно заданному закону с определенной точностью (с допустимой ошибкой).

2. Дискретно-детерминированный подход реализуется с помощью математического аппарата теории автоматов. Система представляется в виде автомата, перерабатывающего дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени. Математической моделью при этом подходе является конечный автомат, характеризующийся конечным множеством X входных сигналов, конечным множеством Y выходных сигналов, конечным множеством Z внутренних состояний, начальным состоянием Z₀ Z; функцией переходов g(z,x); функцией выходов v(z,x). Автомат функционирует в дискретном автоматном времени, моментами которого являются такты (примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния).

Работа конечного автомата происходит по следующей схеме: в каждом t-м такте на вход автомата, находящегося в состоянии z(t), подается некоторый сигнал x(t), на который он реагирует переходом в (t+1)-м такте в новое состояние z(t+1) и выдачей некоторого выходного сигнала. Например, автомат первого рода (автомат Мили) описывается следующим образом:

z(t+1)=g[z(t),x(t)], t=0,1,2,...;

y(t)=v[z(t),x(t)], t=0,1,2,...;

Автомат, для которого функция выходов не зависит от входной переменной x(t), называется автоматом Мура:

y(t)=v[z(t)], t=0,1,2,...

3. Дискретно-стохастический подход использует в качестве математического аппарата вероятностные автоматы, которые можно определить как дискретные потактные преобразователи информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически. Для такого автомата характерно задание таблицы вероятностей перехода автомата в некоторое состояние и появления некоторого выходного сигнала в зависимости от текущего состояния и входного сигнала.

Исследование автомата может проводиться как аналитическими, так и имитационными (например, методом статистического моделирования) методами. Этот подход применим для изучения эксплуатационных характеристик производственных объектов (например, надежности, ремонтопригодности, отказоустойчивости и т.п.).

4. Непрерывно-стохастический подход применяется для формализации процессов обслуживания. Этот подход наиболее известен ввиду того, что большинство производственных (и не только производственных - экономических, технических и т.д.) систем по своей сути являются системами массового обслуживания. Типовой математической схемой моделирования таких систем являются Q-схемы. В обслуживании можно выделить две элементарные составляющие: ожидание обслуживания и собственно обслуживание, а в любой системе массового обслуживания можно выделить элементарный прибор. Соответственно в этом приборе выделяют накопитель (Н) заявок, ожидающих обслуживания, некоторой емкостью; канал обслуживания (К); потоки событий (последовательность событий, происходящих одно за другим в какие-то случайные моменты времени): поток заявок на обслуживание w_i, характеризующийся моментами времени поступления и атрибутами (признаками) заявок (например, приоритетами), и поток обслуживания u_i, характеризующийся моментами начала и окончания обслуживания заявок.

u_i

y_i

w_i

П

 

 

6. Введение в имитационное моделирование систем

 

Известный американский ученый Роберт Шеннон дает следующее определение: "Имитационное моделирование есть процесс конструирования модели реальной системы и постановки экспериментов на этой модели с целью либо понять поведение системы, либо оценить (в рамках ограничений, накладываемых некоторым критерием или совокупностью критериев) различные стратегии, обеспечивающие функционирование данной системы." Все имитационные модели используют принцип черного ящика. Это означает, что они выдают выходной сигнал системы при поступлении в нее некоторого входного сигнала. Поэтому в отличие от аналитических моделей для получения необходимой информации или результатов необходимо осуществлять "прогон" имитационных моделей, т. е. подачу некоторой последовательности сигналов, объектов или данных на вход модели и фиксацию выходной информации, а не "решать" их. Происходит своего рода "выборка" состояний объекта моделирования (состояния - свойства системы в конкретные моменты времени) из пространства (множества) состояний (совокупность всех возможных значений состояний). Насколько репрезентативной окажется эта выборка, настолько результаты моделирования будут соответствовать действительности. Этот вывод показывает важность статистических методов оценки результатов имитации. Таким образом, имитационные модели не формируют свое собственное решение в том виде, в каком это имеет место в аналитических моделях, а могут лишь служить в качестве средства для анализа поведения системы в условиях, которые определяются экспериментатором.

6.1. Проблемы применения имитационного моделирования

Применение имитационного моделирования целесообразно при наличии определенного условия. Эти условия определяет Р. Шеннон:

1. Не существует законченной математической постановки данной задачи, либо еще не разработаны аналитические методы решения сформулированной математической модели. К этой категории относятся многие модели массового обслуживания, связанные с рассмотрением очередей.

2. Аналитические методы имеются, но математические процедуры столь сложны и трудоемки, что имитационное моделирование дает более простой способ решения задачи.

3. Кроме оценки определенных параметров, желательно осуществить на имитационной модели наблюдение за ходом процесса в течение определенного периода.

Дополнительным преимуществом имитационного моделирования можно считать широчайшие возможности его применения в сфере образования и профессиональной подготовки. Разработка и использование имитационной модели позволяет экспериментатору видеть и "разыгрывать" на модели реальные процессы и ситуации.

Необходимо обозначить ряд проблем, возникающих в процессе моделирования систем. Исследователь должен акцентировать на них внимание и попытаться их разрешить, дабы избежать получения недостоверных сведений об изучаемой системе.

Первая проблема, которая касается и аналитических методов моделирования, состоит в нахождении "золотой середины" между упрощением и сложностью системы. По мнению Шеннона искусство моделирования в основном состоит в умении находить и отбрасывать факторы, не влияющие или незначительно влияющие на исследуемые характеристики системы. Нахождение этого "компромисса" во многом зависит от опыта, квалификации и интуиции исследователя. Если модель слишком упрощена и в ней не учтены некоторые существенные факторы, то высока вероятность получить по этой модели ошибочные данные, с другой стороны, если модель сложная и в нее включены факторы, имеющие незначительное влияние на изучаемую систему, то резко повышаются затраты на создание такой модели и возрастает риск ошибки в логической структуре модели. Поэтому перед созданием модели необходимо проделать большой объем работы по анализу структуры системы и взаимосвязей между ее элементами, изучению совокупности входных воздействий, тщательной обработке имеющихся статистических данных об исследуемой системе.

Вторая проблема заключается в искусственном воспроизводстве случайных воздействий окружающей среды. Этот вопрос очень важен, так как большинство динамических производственных систем являются стохастическими, и при их моделировании необходимо качественное несмещенное воспроизведение случайности, в противном случае, результаты, полученные на модели, могут быть смещенными и не соответствовать действительности. Существует два основных направления разрешения этой проблемы: аппаратная и программная (псевдослучайная) генерация случайных последовательностей. При аппаратном способе генерации случайные числа вырабатываются специальным устройством. В качестве физического эффекта, лежащего в основе таких генераторов чисел, чаще всего используются шумы в электронных и полупроводниковых приборах, явления распада радиоактивных элементов и т.д. Недостатками аппаратного способа получения случайных чисел является отсутствие возможности проверки (а значит гарантии) качества последовательности во время моделирования, а также невозможности получения одинаковых последовательностей случайных чисел. Программный способ основан на формировании случайных чисел с помощью специальных алгоритмов. Этот способ наиболее распространен, так как не требует специальных устройств и дает возможность многократного воспроизведения одинаковых последовательностей. Его недостатками являются погрешность в моделировании распределений случайных чисел, вносимую по причине того, что ЭВМ оперирует с n-разрядными числами (т.е. дискретными), и периодичность последовательностей, возникающую в силу их алгоритмического получения. Таким образом, необходима разработка методов улучшения и критериев проверки качества генераторов псевдослучайных последовательностей.

Третьей наиболее сложной проблемой является оценка качества модели и полученных с ее помощью результатов (этап проблема актуальна и для аналитических методов). Адекватность моделей может быть оценена методом экспертных оценок, сравнением с другими моделями (уже подтвердившими свою достоверность), по полученным результатам. В свою очередь, для проверки полученных результатов часть из них сравнивается с уже имеющимися данными.

 

6.2. Принцип Dt и особых состояний dz

 

Задачей имитационного моделирования является получение траектории движения рассматриваемой системы в n – мерном пространстве (Z₁, Z₂, … Z_n), а также вычисление некоторых показателей, зависящих от выходных сигналов системы и характеризующих ее свойства.

В данном случае "движение" системы понимается в общем смысле – как любое изменение, происходящее в ней.

Известны два принципа построения модели процесса функционирования систем: принцип Δt и принцип особых состояний ( ).

Принцип Δt

Предположим, что начальное состояние системы соответствует значениям . Принцип Δt предполагает преобразование модели системы к такому виду, чтобы значения в момент времени t₁= t₀+Δt можно было вычислить через начальные значения , а в момент t₂= t₁+Δt через значения на предшествующем шаге и так для каждого i-ого шага (Δt=const, i=1…M).

Принцип Δt является универсальным, применим для широкого класса систем. Его недостатком является неэкономичность с точки зрения затрат машинного времени. Пример системы, которая моделируется на основе использования принципа Δt – устройство, возводящее в квадрат входной сигнал каждый такт времени или дифференцирующий фильтр.

Принцип особых состояний (принцип ).

При рассмотрении некоторых видов систем можно выделить два вида состояний:

• обычное, в котором система находится большую часть времени, при этом Z_i(t), (i=1 n) изменяются плавно.

• особое, характерное для системы в некоторые моменты времени, причем состояние системы изменяется в эти моменты скачком.

Принцип особых состояний отличается от принципа Δt тем, что шаг по времени в этом случае не постоянен, является величиной случайной и вычисляется в соответствии с информацией о предыдущем особом состоянии.

Примерами систем, имеющих особые состояния, являются системы массового обслуживания. Особые состояния появляются в моменты поступления заявок, в моменты освобождения каналов и т.д.

Для таких систем применение принципа Δt является нерациональным, так как при этом возможны пропуски особых состояний и необходимы методы их обнаружения.

Например, для системы массового обслуживания (Q-схемы) в ка­честве особых состояний могут быть выбраны состояния в моменты поступления заявок на обслуживание в прибор П и в моменты окончания обслуживания заявок каналами К, когда состояние систе­мы, оцениваемое числом находящихся в ней заявок, меняется скач­ком.

Отметим, что характеристики процесса функционирования таких систем с особыми состояниями оцениваются по информации об особых состояниях, а неособые состояния при моделировании не рассматриваются. «Принцип dz » дает возможность для ряда систем существенно уменьшить затраты машинного времени на реализа­цию моделирующих алгоритмов по сравнению с «принципом Dt». Логика построения моделирующего алгоритма, реализующего «принцип dz», отличается от рассмотренной для «принципа Dt» только тем, что включает в себя процедуру определения момента времени t_d, соответствующего следующему особому состоянию си­стемы. Для исследования процесса функционирования больших систем рационально использование комбинированного принципа построения моделирующих алгоритмов, сочетающего в себе пре­имущества каждого из рассмотренных принципов.

 

6.3. Пример использования принципа при моделировании системы

 

Процесс, происходящий в фильтре (рис. 4), описывается дифференциальным уравнением:

 

(1)

 

Рис. 4. Структурная схема дифференцирующего фильтра

 

В уравнении:

K- коэффициент усиления;

х(t) – входной сигнал.

Доказано, что:

Преобразуем математическую модель фильтра к виду, позволяющему применить принцип t. В простейшем случае достаточно уравнение (1) аппроксимировать конечно-разностным уравнением:

Это соответствует итерационной формуле:

(3).

Задав начальное условие Z(t₀)=Z₀ можно построить траекторию процесса, происходящего в фильтре, с целью получения текущего значения производной любой детерминированной функции x(t), подаваемой на вход.

Пример. Пусть шаг =0,01; x(t)=sin(t)+cos(t); Z(0)=0,5; N=1000.

В табл. 1 приведены результаты вычислений. Порядок вычислений следующий.

1. Зададим моменты времени t, в которые вычисляются значения производной (второй столбец в табл. 1).

2. Вычислим: К =1/ =100.

3. Вычислим значения входного сигнала в моменты t: х(t)= sin(t)+cos(t) (третий столбец табл. 1).

4. Вычислим : вычисляется по формуле 2, так как =1, то после преобразования формула 2 имеет вид: ; =0,5 (см. табл. 1).

5. Вычислим -значенияпроизводной в моменты времени t на основе имитационного метода (пятый столбец табл. 1).

6. Вычислим значения производной в моменты времени t на основе аналитического метода по формуле: x’(t)=cos(t)-sin(t) (шестой столбец табл. 1).

7. Построим линейный график траекторий изучаемых процессов. На рис. 5 приведены графики исходной функции x(t) и производных x’(t), рассчитанных имитационным методом и аналитическим.

При построении графика не учитывается первая строка табл. 1, так как значение производной, вычисленной имитационным методом, в момент времени 0 соответствует переходному процессу в дифференцирующем фильтре и поэтому значительно отличается от значения производной, вычисленной аналитически. Продолжительность переходного процесса в фильтре зависит от задания начального значения . В данном случае переходный процесс продолжается один временной такт.

Произвести все расчеты и построить линейный график траекторий изучаемых процессов можно средствами MS Excel.

Таблица 1.

i	t		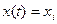	=	x'(t)
			0,5		0,98995
	0,01	1,00995		0,995	0,979801
	0,02	1,019799	1,00995	0,985	0,969555
	0,03	1,029546	1,019799	0,975	0,959211
	0,04	1,039189	1,029546	0,964	0,948771
	0,05	1,048729	1,039189	0,954	0,938237
	0,06	1,058165	1,048729	0,944	0,927608
	0,07	1,067494	1,058165	0,933	0,916887
	0,08	1,076716	1,067494	0,922	0,906074
	0,09	1,085831	1,076716	0,912	0,895171
…	0,1	1,094838	1,085831

 

Рис. 5. Графики траекторий изучаемых процессов: исходной функции x(t) и производных x’(t), рассчитанных имитационным методом и аналитическим

 

Визуальный анализ графика (рис. 5) позволяет сделать вывод о статистической близости результатов, полученных при вычислении производной аналитическим и имитационным методами.

 

6.4. Пример использования принципа особых состояний при моделировании системы

 

Пусть рассматриваемая система – библиотека, в которой работает один библиотекарь. Задан интервал прихода между читателями (равномерный 2-6). Задан интервал обслуживания (равномерный 3-4). Реализовать моделирование работы библиотеки по обслуживанию 100 читателей. Рассчитать среднее время ожидания в очереди и вероятность простоя библиотекаря.

1 шаг. Выберем входные, промежуточные и выходные переменные

входные и промежуточные переменные:

Т инт. прих. – интервал между приходом читателей;

Т инт. обс. – интервал облуживания читателя

Т прих. – момент прихода очередного читателя;

Т нач. обс. – момент начала обслуживания очередного читателя;

Т ок. обс. – момент окончания обслуживания очередного читателя;

выходные переменные:

Т ож. – время ожидания читателя в очереди;

Т простоя – время простоя библиотекаря до прихода очередного читателя;

Т ож.ср. – среднее время ожидания читателя в очереди;

Т простоя – суммарное время простоя библиотекаря;

Р простоя – вероятность простоя библиотекаря.

В табл. 2. и рис. 6 приведены данные ручного моделирования обслуживания первых четырех читателей для иллюстрации принципа особых состояний моделирования системы. Интервалы прихода читателей и интервалы обслуживания заданы произвольно.

Таблица 2. Имитационное моделирование обслуживания читателей

Номер шага (читателя)	T инт. прихода	T инт. обсл	T прихода	T начала. обс.	T ок. обс.	T ожидания в очереди	T простоя библиот.
…

Рис. 6.

 

2 шаг. Разработка блок-схемы алгоритма имитации СМО (рис. 7)

3 шаг. В соответствии с разработанной блок-схемой составляется программа имитации работы СМО на любом языке программирования с использованием любых программных средств.

4 шаг. Расчет показателей эффективности СМО с помощью разработанной программы имитации.

5 шаг. Анализ полученных результатов, оценка эффективности СМО.

 

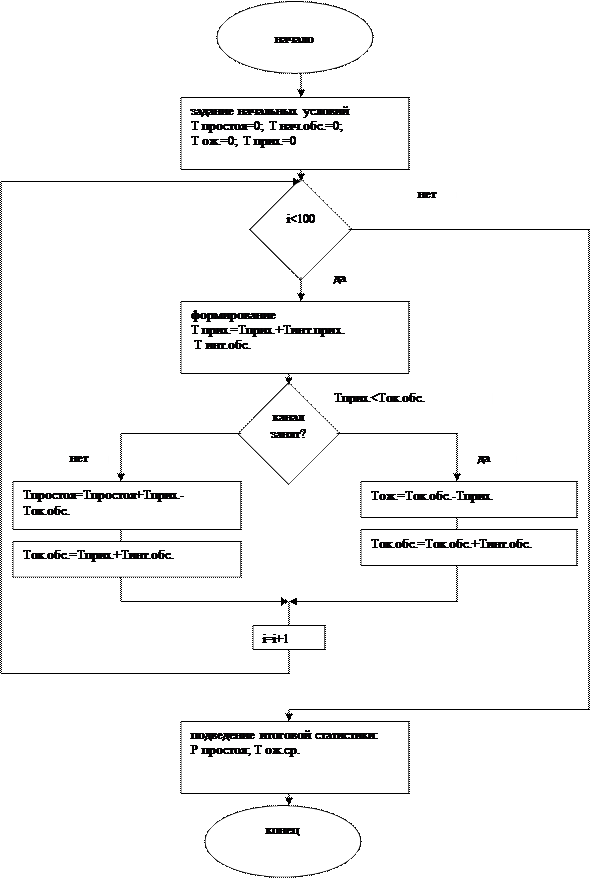
Рис. 7. Блок-схема алгоритма имитации работы СМО

 

 

7. Математические основы имитационного моделирования

7.1. Методы генерации случайных чисел

 

Существует три способа генерации случайных чисел:

1. Аппаратный - в основе лежит какой-либо физический эффект (например, шумы в электронных устройствах, случайные числа вырабатываются с помощью специального датчика. Этот способ не гарантирует качество последовательности случайных чисел непосредственно во время моделирования. С помощью этого способа нельзя получать одинаковые последовательности. Используется редко.

2. Табличные - случайные числа оформлены в виде таблицы в оперативной памяти или на внешнем носителе. При этом способе запас чисел ограничен, вычислительные ресурсы используются неэффективно. Используется редко.

3. Программный (алгоритмический) - случайные числа формируются с помощью специальных программ. Каждое случайное число вычисляется с помощью соответствующей программы по мере возникновения потребностей при моделировании системы на ЭВМ. Этот способ наиболее распространен.

Программная имитация случайных воздействий сводится к генерированию некоторых стандартных (базовых) процессов и к их последующему функциональному преобразованию. Чаще всего в качестве базовой последовательности используют независимые случайные величины, равномерно распределенные на интервале (0,1).

Непрерывная случайная величина имеет равномерное распределение в интервале (a,b), если ее функции плотности и распределения соответственно примут вид

Для получения случайных чисел на ЭВМ используются алгоритмы, поэтому такие последовтельности, являющиеся по сути детерминированными, называются псевдослучайными. ЭВМ оперирует n-разрядными числами, поэтому поэтому на ЭВМ вместо непрерывной совокупности равномерных случайных чисел интервала (0,1) используют дискретную последовательность 2ⁿ случайных чисел того же интервала - закон распределения такой дискретной последовательности называется квазиравномерны распределением.

Требования к идеальному генератору случайных чисел:

1. Последовательность должна состоять из квазиравномернло распределенных чисел.

2. Числа должны быть независимыми.

3. Последовательности случайных чисел должны быть воспроизводимыми.

4. Последовательности должны иметь неповторяющиеся числа.

5. Последовательности должны получаться с минимальными затратами вычислительных ресурсов.

Наибольшее применение в практике моделирования на ЭВМ для генерации последовательностей псевдослучайных числе находят алгоритмы вида:

x_i+1=Ф(x_i),

представляющие собой реккурентные соотношения первого порядка.

Одна из первых процедур исторически сложившихся – метод серединных квадратов.

Пример. x₀ = 0,2152, (x₀)²=0,04631104, x₁ = 0,6311, (x₁)²=0,39828721, x₂=0,8287 и т.д. Пусть имеется 2n-разрядное число меньше 1, возведем его в квадрат, а затем отберем средние 2n разрядов.

Недостаток подобных методов - наличие корреляции между числами последовательности, а иногда случайность вообще отсутствует, например:

x₀ = 0,4500, (x₀)²=0,20250000, x₁ = 0,2500, (x₁)²=0,06250000, x₂=0,2500 и т.д.

Широкое применение получили конгруэнтные процедуры генерации псевдослучайных последовательностей.

В основе лежит понятие конгруэнтности. Два целых числа a и b конгруэнтны (сравнимы) по модулю m, где m - целое число, тогда и только тогда, когда существует такое целое число k, что a-b=km, т.е. если разность делится на m и если числа a и b дают одинаковые остатки от деления на абсолютную величину числа m.

Пример: a=9375 и b=1875: 9375-1875=7500=4*1875

9375-6875=2500=4*625.

Большинство конгруэнтных процедур генерации случайных чисел основаны на следующей формуле:

где - неотрицательные целые числа.

По целым числам последовательности {X_i} можно построить последовательность {x_i}={X_i/M} рациональных чисел из единичного интервала (0,1).

Конгруэнтная процедура получения последовательности псевдослучайных чисел квазиравномерно распределенных чисел может быть реализована мультипликативным или смешанным методом.

Мультипликативный метод.

Задает последовательность неотрицательных целых чисел {X_i} не превосходящих М по формуле:

,

где - неотрицательные целые числа.

Выражение означает: 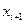равен остатку от деления на M.

В силу детерминированности метода получают воспроизводимые последовательности.

В качестве X₀ выбирают произвольное нечетное число; М – число определяющее, наибольшее значение получаемых случайных чисел, при машинной реализации 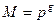, р – основание системы счисления, g – число бит в машинном слове.

Для р=2алгоритм:

1. вычислить коэффициент , где t – любое целое положительное число;

2. найти произведение взять g младших разрядов в качестве первого члена последовательности , а остальные отбросить.

3. определить дробь из интервала (0,1)

4. присвоить 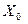= и вернуться к п.2.

Пример (для двоичной системы счисления): X₀=0111 (7 в десятичной), t=1, или 5 (пусть будет пять - 0101), М=16, g=4

1.) =(0101)(0111)=00100011 (35), =0011(3), 3/16=0,1875 или x₁=7*5(mod 16)=0,1875

2.) =(0101)(0011)=00001111 (15), =1111 (15),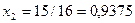

Полученные числа конгруэнтны.

Смешанный метод.

Задает последовательность неотрицательных целых чисел {X_i} не превосходящих М по формуле:

,

где - неотрицательные целые числа.

С вычислительной точки зрения метод сложнее, но введение дополнительного параметра позволяет уменьшить возможную корреляцию между генерируемыми числами.

В настоящее время почти все библиотеки стандартных программ для вычисления последовательностей равномерно распределенных СЧ основаны на конгруэнтной процедуре.

Применяемые генераторы случайных чисел перед моделированием должны пройти тщательное предварительное тестирование на равномерность, стохастичность и независимость получаемых последовательностей случайных чисел.

Методы улучшения качества последовательностей случайных чисел:

Один из методов: использование рекуррентных формул порядка r:

Но применение этого способа приводит к увеличению затрат вычислительных ресурсов на получение чисел.

 

7.2. Методы имитационного моделирования случайных величин

 

Моделирование непрерывной случайной величины. Метод обратной функции

Для получения непрерывных случайных величин с заданным законом распределения, как и для дискретных величин, можно воспользоваться методом обратной функции. Если случайная величина Y имеет плотность распределения f(y), то распределение случайной величины

является равномерным на интервале (0,1). Чтобы получить число, принадлежащее последовательности случайных чисел {y_i}, имеющих функцию плотности f(y), необходимо разрешить относительно y_i уравнение

где x_i - число, принадлежащее последовательности случайных чисел равномерно распределенных на интервале от (0,1).

Пример. Необходимо получить случайные числа с показательным (экспоненциальным) законом распределения (например, интервалов времени между поступлениями заявок на обслуживание):

.

- случайное число, имеющее равномерное распределение на интервале (0,1). Тогда

Этот способ получения случайных чисел с заданным законом распределения имеет ограниченную сферу применения, так как для многих законов распределения, встречающихся в практических задачах моделирования, интеграл не берется, т.е. приходится прибегать к численным методам решения, что увеличивает затраты вычислительных ресурсов на получение каждого числа; даже для случаев, когда интеграл берется в конечном виде получаются формулы, содержащие действия логарифмирования, извлечения корня и т.д., что также резко увеличивает затраты машинного времени на получение каждого случайного числа. Поэтому на практике часто пользуются приближенными способами преобразования случайных чисел, которые можно классифицировать следующим образом:

а) универсальные способы, с помощью которых можно получать случайные числа с законом распределения любого вида; б) неуниверсальные способы, пригодные для получения случайных чисел с конкретным законом распределения.

Метод, основанный на кусочной аппроксимации функции плотности распределения. Рассмотрим приближенный универсальный способ получения случайных чисел, основанный на кусочной аппроксимации функции плотности.

Пусть требуется получить последовательность случайных чисел { y_j } с функцией плотности f_h(y), значения которой лежат в интервале (a,b). Разобъем интервал (a,b) на m интервалов (рис. 8), и будем считать f_h(y) на каждом интервале постоянной. Разбивать необходимо так, чтобы вероятность попадания случайной величины в любой интервал (a_k, a_k+1) была постоянной, т.е.:

 

Рис. 8. Кусочная аппроксимация функции плотности

В таком случае, алгоритм этого способа получения случайных чисел сводится к выполнению следующих действий:

1) Генерируется случайное равномерно распределенной число x_i из интервала (0,1);

2) с помощью этого числа выбирается интервал (a_k, a_k+1);

3) генерируется число x_i+1 ;

4) вычисляется случайное число y_j =a_k+ x_i+1 (a_k+1-a_k) с требуемым законом распределения.

Рассмотрим пример применения способа преобразования последовательности равномерно распределенных случайных чисел {x_i} в последовательность с заданным законом распределения {y_i} на основе предельных теорем теории вероятностей. Такие способы ориентированы на получение последовательностей чисел с конкретным законом распределения, т.е. не являются универсальными.

Приближенный метод генерации последовательности значений нормально распределенной СВ. Пусть требуется получить последовательность случайных чисел {y_i}, имеющих нормальное распределение с математическим ожиданием m и средним квадратическим отклонением s:

 

Рис. 9. Вид нормального распределения

 

Будем формировать случайные числа t_j в виде сумм последовательностей случайных чисел {x_i}, равномерно распределенных на интервале от (0,1). Можно воспользоваться центральной предельной теоремой: Если X₁ , X₂,..., X_n - независимые одинаково распределенные случайные величины, имеющие математическое ожидание M(X_i)=a и дисперсию s², то при N ® ¥ сумма асимптотически нормальна с математическим ожиданием Na и средним квадратическим отклонением . Практически достаточно N=8¸12, а в простейших случаях - 4¸5. Преимущество этого способа - высокое быстродействие. Недос­татком является игнорирование «хвостов» нормального распределе­ния, которые могут уходить в обе стороны от величины т на рас­стояние, превышающее 6 s. Поэтому при проведении особо точных экспериментов применяются другие - более точные (но более мед­ленные) способы. В современных системах имитационного моделирования обычно используются не менее двух программных датчи­ков случайных величин, распределенных по нормальному закону (их выбор осуществляется автоматически управляющей программой).

Метод Неймана. Метод Неймана является универсальным. Единственным ограничением его применения является то, что СВ должна задаваться усеченным законом, или законом, который может быть аппроксимирован усеченным.

Рис. 10.

На рис. 10 изображено - функция плотности распределения случайной величины , заданная на интервале . Максимальное значение функции обозначено W.

Метод состоит в следующем:

1. С помощью датчика случайных чисел, равномерно распределенных на интервале (0,1), выбирают пары чисел . (точка на рис. 4).

2. Формируется преобразованная пара чисел, равномерно распределенных на интервале соответственно и :

Проверяется выполнение неравенства

Если оно выполнено, то и есть искомое значение случайной величины . На рис. 10 это соответствует первой координате точки . В противном случае вновь генерируются случайные числа и алгоритм повторяется заново.

 

7.3. Имитационное моделирование случайных событий

 

Имитация элементарного события. Необходимо реализовать случайное событие А, наступающее с заданной вероятностью p. Определим А как событие, состоящее в том, что выбранное значение x_i равномерно распределенной на интервале (0,1) случайной величины удовлетворяет неравенству:

x_i =<p.

Тогда вероятность события А будет Противоположное событие состоит в том, что x_i >p, его вероятность равна 1-р.

Имитация полной группы событий. Рассмотрим группу событий. Пусть А₁, А₂ ,..., А_s - полная группа событий, наступающих с вероятностями p₁, p₂ ,..., p_s соответственно. Определим событие А_m как событие, состоящее в том, что выбранное значение x_i случайной величины удовлетворяет неравенству

,

где

Процедура моделирования испытаний в этом случае состоит в последовательном сравнении случайных чисел x_i со значениями l_r. Если условие выполняется, исходом испытания оказывается событие А_m.

<