Электронно-дырочным переходом, или р-n-переходом, называют переходный слой, возникающий при контакте двух полупроводников с различным типом электропроводности. Получить p-n-переход непосредственным соприкосновением двух полупроводников практически невозможно, так как на их поверхности содержится огромное количество примесей, загрязнений и всевозможных дефектов, резко меняющих свойства полупроводника. Для создания р-n-переходов используют различные технологические приемы, изменяющие тип электропроводности той или иной области монокристалла. Например, путем диффузии в монокристалл р-типа донорных примесей можно получить в нем область n-типа (рис. 1.61, а), расположенную левее сечения х0.
Широко применяют также выращивание на поверхности кристалла монокристаллического слоя, повторяющего кристаллографическую ориентацию кристалла, но имеющего противоположный тип электропроводности (рис. 1.61, б), такие слои называют эпитаксиальными. Границу х0, разделяющую п- и р-области монокристалла, называют металлургической границей. Если на границе раздела концентрация примесей скачком изменяется от Nd к Na что имеет место при эпитаксиальном наращивании слоев, то такой переход называют резким. Если вблизи металлургической границы концентрация примеси изменяется плавно, что имеет место при диффузии примеси, то такой переход называют плавным.
Если п- и р-области каким-либо образом разделены, то их энергетические диаграммы имеют вид, показанный на рис. 1.62, а. В этом случае уровни Ферми разнесены на величину ЕПО = EFn - EFp. При осуществлении металлургического контакта между п- и p-областями (рис. 1.62, 6) вследствие различия концентраций однотипных носителей заряда возникают диффузионные потоки электронов из n-области в р-область и дырок из р-области в «-область. При этом n-область заряжается положительно, ар-область отрицательно, что приводит к понижению всех энергетических уровней, в том числе и уровня Ферми в n-области, и повышению их в р-области. Диффузия электронов слева направо и дырок справа налево происходит до тех пор, пока постепенно поднимающийся уровень Ферми в р-области не установится на одной высоте с постепенно опускающимся уровнем Ферми в n-области. В результате энергетическая диаграмма примет вид, показанный на рис. 1.62, в, при этом на границе раздела образуется энергетический барьер, высота которого равна разности уровней Ферми в неконтактируемом состоянии полупроводников:
(1.75)
Следствием диффузионного перемещения электронов и дырок является уменьшение их концентрации вблизи границы раздела x0 (рис. 1.62, г), в результате чего между сечениями хn и хр образуется обедненный подвижными носителями заряда слой, в котором расположены положительные заряды доноров и отрицательные заряды акцепторов (рис. 1.62, д). Эти заряды создают внутреннее электрическое поле, препятствующее диффузии электронов и дырок. Значения этих зарядов таковы, что обеспечивают равенство уровней Ферми в контактируемых областях. Электрическое поле, создаваемое зарядами доноров и акцепторов, характеризуют высотой потенциального барьера φ к0, напряженностью поля ζ (х) и распределением потенциала φ(х). Высота потенциального барьера связана с высотой энергетического барьера соотношением
(1.76)
Для нахождения распределения потенциала φ(х) и напряженности поля ζ (х) воспользуемся уравнением Пуассона:
(1.77)
Учтем, что концентрация подвижных носителей в p-n-переходе существенно меньше концентрации примесных атомов Nd и Na.. Тогда для n-области ρ( х) = q*Nd,, а для р-области ρ(х) =-q*Na. Проинтегрируем уравнение Пуассона раздельно для п- и р-областей.
Для n-области (хп < х < х0)
(1.78)
Для р-области (х0 < х < хр)
(1.79)
То есть распределение напряженности поля в переходе выражается кусочно-линейной функцией (рис. 1.62, e ). Она равна нулю при х>хр и х <хп и максимальна при х=х0:
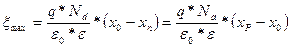(1.80)
Интегрируя ζ(х) в интервале от хп до ха, получим функцию распределения потенциала φ(х) в этой области:
(1.81)
Интегрируя ζ (х)в интервале от х0 до хр, получим
(1.82)
Следовательно, функция φ(x) состоит из двух параболических участков и имеет точку перегиба при х = х0 (рис. 1.62, ж).
Для нахождения ширины перехода Δо = (хр – хn) приравняем (1.81) и (1.82) при х = х0. Тогда, учитывая, что φ (хп) - φ(хр) = φK0, получим:
(1.83)
Учитывая (1.80) и то, что Δо = (х0 - хп) + (хр - х0), получим:
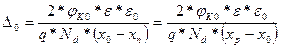(1.84)
Отсюда получим:
(1.85)
(1.86)
Следовательно
(1.87)
Из уравнений (1.85) и (1.86) следует, что при Nd = Na выполняется условие х0 – xn = хp - х0. Такой переход называют симметричным. Если Nd ≠ NA, то такой переход называют несимметричным. В этом случае переход оказывается сдвинутым в область с более низкой концентрацией примесей. При Nd >> Na уравнение (1.87) принимает вид
(1.87,a)
При Nd << Na., уравнение (1.87) принимает вид
(1.87,б)
Электроны (и дырки), находясь в хаотическом движении, способны перемещаться через электронно-дырочный переход из одной области полупроводникового кристалла в другую, создавая потоки носителей заряда, обозначенные на рис. 1.62 цифрами от 1 до 4. Потоки 1 и 3 называют потоками основных носителей заряда (ПОН), потоки 2 и 4 — потоками неосновных носителей заряда (ПНН). Для ПОН поле в переходе является тормозящим. Поэтому переходить из n-области в р-область могут только те электроны, энергия которых выше Еcn, и, соответственно, переходить из р-области в n-область могут только те дырки, энергия которых ниже уровня Evn Для ПНН поле в переходе является ускоряющим, поэтому все неосновные носители заряда способны перемещаться из одной области в другую. При отсутствии на переходе внешнего напряжения ПОН и ПНН уравновешивают друг друга, поэтому ток через переход равен нулю.
Если к переходу подключено внешнее напряжение плюсом к р-области, то создаваемое им электрическое поле противоположно по направлению внутреннему электрическому полю. В этом случае потенциальный барьер в р-n-переходе уменьшается. При противоположной полярности внешнего напряжения потенциальный барьер повышается. Внешнее напряжение, уменьшающее высоту потенциального барьера в p-n-переходе, называют прямым, а напряжение, повышающее высоту барьера, — обратным. В дальнейшем прямое напряжение будем считать положительным, а обратное — отрицательным. Внешнее напряжение практически полностью прикладывается непосредственно к р-п -переходу, так как он обеднен подвижными носителями зарядов и имеет высокое по сравнению с другими областями структуры электрическое сопротивление. Поэтому изменение высоты потенциального барьера равно приложенному напряжению и, и высоту потенциального барьера в р-n-переходе следует определять по формуле
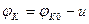
Если к р-n-переходу приложено прямое напряжение, то вследствие уменьшения высоты потенциального барьера возрастает количество основных носителей заряда, перемещающихся через р-n-переход. В результате появляется большой прямой ток, создаваемый потоками 1 и 3. Если к p-n-переходуприложено обратное напряжение, то количество основных носителей заряда, перемещающихся через переход, становится равным нулю, и через переход течет небольшой обратный ток, создаваемый потоками неосновных носителей заряда (потоки 2 и 4). Таким образом, изменяя приложенное к р-n-переходу напряжение, можно изменять ток и его направление. При изменении приложенного к переходу внешнего напряжения одновременно с изменением высоты потенциального барьера изменяется ширина перехода. В этом случае в (1.87), (1.87а) и (1.876) вместо φK0 следует подставлять φк. При подаче прямого напряжения переход сужается, а при подаче обратного напряжения расширяется.
