Распределение концентрации неравновесных носителей заряда

Увеличение концентрации электронов на поверхности дырочного полупровод­ника, вызванное инжекцией, ведет к появлению диффузионного электронного потока, направленного вдоль оси х, перпендикулярной поверхности полупровод­ника, в результате чего концентрация электронов возрастает не только на поверх­ности, но и в глубине полупроводника. При этом инжектированные электроны углубляются в полупроводник на разные расстояния. Для нахождения закона изменения избыточной концентрации электронов вдоль оси х выделим внутри полупроводника элементарный объем, ограниченный сечениями х₁ и х₂, перпен­дикулярными оси х, приняв площадь сечений равной 1 см² (рис. 1.49). Тогда ве­личина этого объема будет равна dx, В этот объем входит некоторое количество электронов N₁(x₁), часть электронов рекомбинирует с дырками, а некоторое ко­личество N₂(x₂) покидает этот объем.

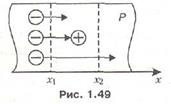
Из молекулярной физики известно, что количество частиц, диффундирующих в единицу времени через единичную площадку, перпендикулярную направлению диффузии, пропорционально градиенту концентрации этих частиц. Исходя из этого и учитывая, что количество диффундирующих частиц может меняться с течением времени, можно определить количество электронов, диффундирующих через любое сечение х за время dt.

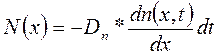(1.60)

Здесь D_n — коэффициент диффузии электронов, определяющий количество диф­фундирующих электронов в единицу времени при единичном градиенте концен­трации и измеряемый в квадратных сантиметрах в секунду.

Аналогичным образом определяется количество диффундирующих дырок:

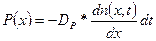(1.61)

Знак «минус» в уравнениях (1.60) и (1.61) указывает на то, что перемещение но­сителей заряда происходит в сторону убывания их концентрации.

Зная количество электронов, диффундирующих через сечения х₁ и х₂, и учитывая, что в объеме dx происходит рекомбинация со скоростью, определяемой уравнени­ем (1.56), можно найти изменение количества электронов в объеме dx за время dt

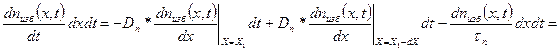
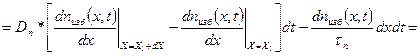
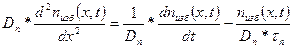
Последнее уравнение можно записать в виде

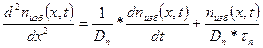
Избыточные электроны диффундируют на расстояние 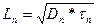за время жиз­ни τ_n, поэтому

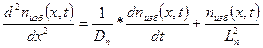(1.62)

Полученное уравнение называется уравнением непрерывности для электронов. Оно характеризует изменение избыточной концентрации электронов, обуслов­ленное диффузией и рекомбинацией. Интегрируя это уравнение при известных начальных и граничных условиях, можно найти n_изб(x,t). Аналогичное уравнение можно получить и для дырок, инжектированных в электронный полупроводник.

В случае, когда уменьшение концентрации электронов в элементарном объеме, вызванное рекомбинацией, компенсируется инжекцией в него новых электронов, избыточная концентрация электронов сохраняется неизменной во времени. Тогда уравнение (1.62) должно быть записано в виде

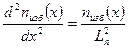(1.63)

Решение этого уравнения имеет вид

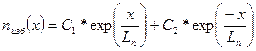
Постоянные интегрирования С₁ и С₂ находят из следующих условий:

,

.

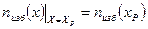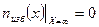Здесь п_изб(х_Р) — концентрация электронов на поверхности полупроводника, вели­чина которой обычно известна.

Следовательно, 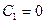и 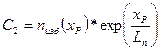. Тогда

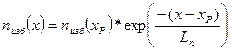(1.64)

Таким образом, избыточная концентрация электронов изменяется вдоль оси х по экспоненциальному закону, а величина L_n, называемая диффузионной длиной, представляет собой расстояние, на котором избыточная концентрация уменьша­ется в е раз (рис. 1.50).

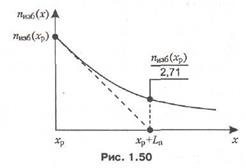
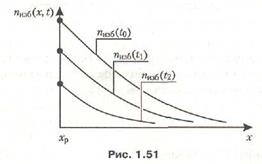
При прекращении инжекции избыточная концентрация электронов с течением времени будет уменьшаться в соответствии с уравнением (1.57), что отражено на рис. 1.51, где показаны распределения концентрации в различные моменты времени.

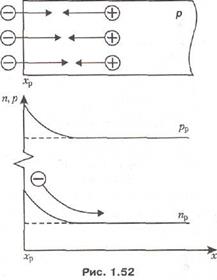
Распределение избыточной концентрации дырок при инжекции электронов в дырочный полупроводник имеет такой же характер, как и распределение избы­точной концентрации электронов (рис. 1.52), однако физические причины, вызы­вающие увеличение концентрации электронов и дырок, различны. Возрастание концентрации электронов вызвано инжекцией электронов в полупроводник из внешней цепи, а возрастание концентрации дырок вызвано возникновением внут­реннего поля, которое притягивает дырки из глубины полупроводника. В итоге возникает градиент концентрации как электронов, так и дырок. Из-за наличия градиента концентрации электроны диффундируют вглубь полупроводника, встречаются с дырками и рекомбинируют с ними. На смену рекомбинировавшим электронам из внешней цепи поступают новые электроны, а на смену рекомбинировашим дыркам из глубины полупроводника поступают новые дырки. Казалось бы, что одновременно с диффузией электронов должна существовать и диффу­зия дырок, так как имеется градиент концентрации дырок, однако этого не проис­ходит. Объясняется это тем, что диффузия дырок, если бы она возникла, привела бы к увеличению напряженности внутреннего электрического поля, которое вер­нуло бы Дырки назад, то есть стремление дырок к диффузии уравновешивается силами внутреннего электрического поля.

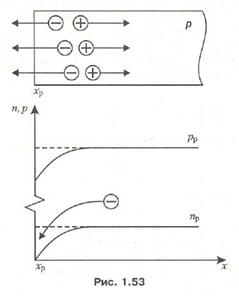
При экстракции электронов из дырочного полупроводника (рис. 1.53) протека­ют похожие процессы: уменьшается концентрация электронов на поверхности полупроводника, появляется градиент концентрации и как следствие возникает диффузия электронов. Поскольку электроны в дырочном полупроводнике обра­зуются в результате тепловой генерации одновременно с дырками, то экстракция электронов ведет к нарушению электронейтральности и возникновению внутрен­него поля, которое сдвигает дырки от поверхности вглубь полупроводника.

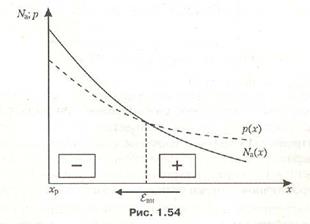
Внутреннее электрическое поле в полупроводнике, препятствующее диффузии основных носителей заряда, возникает не только при инжекции или экстракции неосновных носителей заряда. Оно появляется также в полупроводниках с нерав­номерным распределением примеси. На рис. 1.54 представлен случай, когда кон­центрация акцепторной примеси N_a(x) убывает в направлении оси х. Полагая, что все акцепторы ионизированы, можно считать, что р(х) = N_a(x), то есть закон изме­нения концентрации дырок такой же, как закон изменения концентрации приме­сей. При этом должна возникать диффузия дырок, в результате которой их концентрация у поверхности полупроводника снизится, а в глубине возрастет, что приведет к возникновению внутреннего электрического поля, препятствующего диффузии дырок. Если в такой полупроводник через сечение х_р инжектировать электроны, то перемещение электронов будет происходить как в результате диф­фузии, так и под действием сил поля.

Токи в полупроводниках

В общем случае движение носителей заряда в полупроводнике обусловлено дву­мя процессами: дрейфом под действием сил поля и диффузией из-за наличия градиента концентрации. Ток, возникающий под действием сил поля, называют током проводимости. Ток, обусловленный градиентом концентрации, называют током диффузии. Учитывая то, что перемешаются как электроны, так и дырки, плотность полного тока должна содержать четыре составляющих:

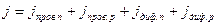
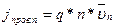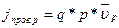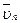Плотность электронного тока проводимости равна , а плотность ды­рочного тока проводимости равна , где и 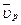— средние направлен­ные скорости движения электронов и дырок соответственно.

Средняя скорость дрейфа носителей заряда определяется ускорением а и сред­ним временем пробега τ:

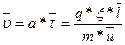
Это уравнение можно представить в более простом виде:

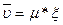(1.65)

где ζ — напряженность поля;

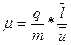- подвижность носителей заряда, определяемая средней длиной сво­бодного пробега 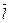и средней тепловой скоростью .

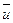Таким образом, плотность электронного тока проводимости равна

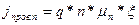(1.66)

Плотность дырочного тока проводимости равна

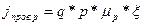(1.67)

Результирующая плотность тока проводимости равна

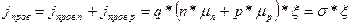(1.68)

Здесь 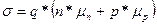— удельная электрическая проводимость полупровод­ника.

В собственном полупроводнике n_i =р_i поэтому

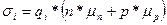(1.69)

У электронного полупроводника п_п >> р _n, поэтому

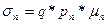(1.70)

У дырочного полупроводника р_р >> n _р поэтому

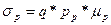(1.71)

Из приведенных уравнений следует, что удельная электрическая проводи­мость полупроводника определяется концентрацией и подвижностью носите­лей заряда.

При комнатной температуре подвижность электронов в германии составляет 3900 см²/(В^*с), а в кремнии 1400 см²/(В*с), подвижность дырок в германии равна 1900 см²/(В-с), а в кремнии 500 см²/(В*с). С повышением температуры уменьша­ется длина свободного пробега носителей заряда 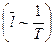и возрастает тепловая скорость движения носителей заряда 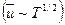, Поэтому с ростом температуры подвижность убывает по закону 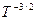. Зная зависимость подвижности и концент­рации носителей заряда от температуры, можно установить температурную зави­симость проводимости (рис. 1.55), которая в основном подобна температурной за­висимости концентрации носителей заряда, приведенной ранее на рис. 1.47.

В области низких температур σ_n и σ_р возрастают с ростом температуры из-за уве­личения числа ионизированных примесных атомов. В рабочем интервале темпе­ратур концентрация носителей заряда сохраняется приблизительно постоянной и равной концентрации примеси, а подвижность уменьшается, поэтому умень­шаются σ_n и σ_p. В области высоких температур резко увеличивается тепловая генерация носителей заряда, и снижение подвижности не играет существенной роли. Удельная электрическая проводимость собственного полупроводника зави­сит от температуры по экспоненциальному закону, и уменьшение подвижности не имеет принципиального значения. При невысокой концентрации примеси (до 10¹⁵-10¹⁹ см^-3) подвижность практически не зависит от величины концентрации. При более высокой концентрации примеси ионизированные примесные атомы со­здают вокруг себя кулоновское поле, искривляющее траектории движения носи­телей заряда, в результате чего уменьшается длина свободного пробега и соответ­ственно подвижность носителей заряда. При изменении концентрации примеси от 10¹⁵ до 10¹⁹ см^-3 подвижность уменьшается примерно на порядок.

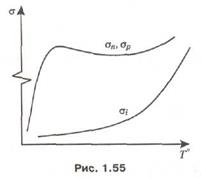
Особую роль играет зависимость подвижности от напряженности поля, так как при этом зависимость между скоростью движения носителей заряда и напряжен­ностью поля становится нелинейной (рис. 1.56). В слабых электрических полях (ζ< 10³ В/см) носители заряда на длине свободного пробега приобретают отно­сительно малую энергию, не превышающую тепловую энергию 3/2 К*Т. При этом результирующая скорость носителей заряда примерно равна тепловой. При таких условиях подвижность сохраняется постоянной, а скорость дрейфа линейно на­растает с ростом напряженности поля. При напряженности поля более 10³ В/см скорость дрейфа становится соизмеримой со скоростью теплового движения, вследствие чего увеличивается результирующая скорость движения носителей заряда, происходит как бы разогрев электронно-дырочного газа, Такие носители заряда, энергия которых сравнима или превышает тепловую энергию 3/2 К*Т, на­зывают горячими. В этих условиях с увеличением напряженности поля уменьша­ется длина свободного пробега, вследствие чего подвижность носителей заряда уменьшается обратно пропорционально напряженности поля, а дрейфовая ско­рость возрастает прямо пропорционально квадратному корню из напряженности поля. Если напряженность поля превышает критическое значение ζ_пр. - 10⁴ В/см, то с ростом ζ подвижность уменьшается обратно пропорционально напряжен­ности поля, _а дрейфовая скорость сохраняется неизменной и равной скорости насыщения υ_нас = 10⁷ см/с. Скорость дрейфа не может быть выше скорости насы­щения.

Ток_диффузии результате неравномерного распределения концентра­ции носителей заряда. Этот ток пропорционален градиенту концентрации носите­лей заряда. Плотность тока диффузии определяется количеством диффундиру­ющих частиц в единицу времени через единичную площадку, перпендикулярную направлению диффузии:

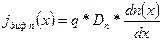(1.72)

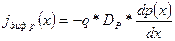(1.73)

где D_n — коэффициент диффузии электронов, равный 99 см²/с для германия и 34 см²/с для кремния;

D_P — коэффициент диффузии дырок, равный 43 см²/с для германия и 13 см²/с для кремния.

Параметры диффузионного и дрейфового движения связаны между собой соот­ношениями Эйнштейна:

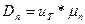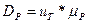; (1.74)

где 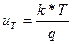средняя скорость теплового движения, В; если Т = 300 К, то и_T =0,0256 B, кТ=0,0256эВ.

Рассматривая результирующий ток как сумму отдельных составляющих тока, будем руководствоваться следующими формальными принципами:

□ если существует поле, то должен существовать ток проводимости независимо от наличия тока диффузии;

□ если существует градиент концентрации, то должен существовать ток диффузии независимо от наличия тока проводимости.

Исходя из этих принципов, можно построить графики распределения отдельных составляющих результирующего тока вдоль оси х при инжекции электронов в ды­рочный полупроводник. Током проводимости электронов ввиду их невысокой концентрации можно пренебречь. Такое распределение отдельных составляющих тока показано на рис. 1.57, а. Дырочный ток формально состоит из тока проводимости и тока диффузии:

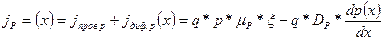
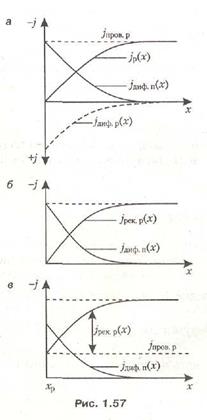
Суммарный дырочный ток 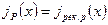показан на рис. 1.57, б. Физически воз­никновение дырочного тока при инжекции электронов в дырочный полупровод­ник обусловлено притяжением дырок инжектированными электронами, при этом дырки, притягиваемые инжектированными электронами, встречаясь с ними, рекомбинируют. Поэтому дырочный ток в случае инжекции электронов называют током рекомбинации.

Внутреннее электрическое поле в полупроводнике возникает не только при ин­жекции (или экстракции) неосновных носителей заряда, но и при введении (или выведении) основных носителей заряда. Так, при выведении через сечение х_Р ды­рок отрицательные заряды акцепторов на левом конце полупроводника оказыва­ются некомпенсированными, возникает внутреннее электрическое поле и на сме­ну ушедшим дыркам из глубины полупроводника поступают новые, в результате чего появляется ток проводимости j_пров.р и распределение токов принимает вид, показанный на рис. 1.57, в.

При экстракции электронов из дырочного полупроводника (см. рис. 1.53) ток диффузии электронов изменяет свое направление. При этом также возникает внутреннее электрическое поле, ведущее к возникновению дырочного тока, кото­рый называют током генерации (рис. 1.58).

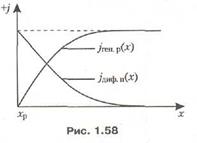
Аналогичные процессы происходят и в электронном полупроводнике при инжек­ции (или экстракции) в него дырок, с той лишь разницей, что электроны и дырки меняются ролями.

Поверхностные явления

Периодичность кристаллической решетки полупроводникового монокристалла нарушается на его поверхности. У каждого поверхностного атома один из сосед­них атомов отсутствует, из-за чего в запрещенной зоне энергетической диаграм­мы приповерхностной области полупроводника появляются разрешенные энер­гетические уровни. Эти дополнительные уровни, теоретически предсказанные советским академиком И. Е. Таммом, называют уровнями Тамма. Плотность по­верхностных уровней равна плотности поверхностных атомов, то есть около 10¹⁵ см^-2. Уровни, расположенные вблизи зоны проводимости, называют донорными. Они возникают при потере поверхностными атомами электронов, в резуль­тате чего поверхностные атомы приобретают положительный заряд. Уровни, рас­положенные вблизи валентной зоны, называют акцепторными. Они образуются при захвате поверхностными атомами чужих электронов, в результате чего по­верхностные атомы приобретают отрицательный заряд.

На поверхности реального полупроводника всегда имеются адсорбированные примеси и оксид, наличие которых маскирует уровни Тамма, снижая их плот­ность до 10¹⁰-10¹¹ см^-2. Тип поверхностных уровней зависит от обработки по­верхности полупроводника. Так, например, при обработке поверхности элект­ронного полупроводника в атмосфере кислорода или озона на его поверхности образуются акцепторные уровни. При обработке поверхности дырочного полу­проводника парами воды преобладают донорные уровни. При нанесении на по­верхность полупроводника пленки оксида SiO₂ вблизи границы раздела с крем­нием возникает тонкий переходный слой, образованный положительным зарядом ионов кремния.

Поверхностные уровни являются причиной возникновения в приповерхностном слое полупроводника электрического поля, характер и интенсивность которого зависят от типа и плотности поверхностных уровней. Если на поверхности элек­тронного полупроводника преобладают донорные уровни, то она заряжается по­ложительно и к поверхности притягиваются отрицательные заряды, в результате чего возникает обогащенный электронами приповерхностный слой, концент­рация электронов в котором выше, чем в объеме полупроводника (рис. 1.59, а), и происходит изгиб вниз границ энергетических зон.

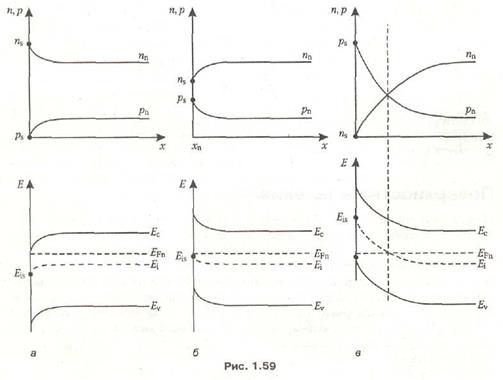
Поверхностная концентрация электронов и дырок в этом случае может быть рас­считана по формулам (1.42) и (1.43), которые принимают вид

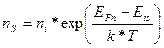
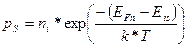
где E_is энергетический уровень, соответствующий середине запрещенной зоны на поверхности полупроводника.

На поверхности полупроводника сохраняется равновесное состояние, то есть выполняется условие 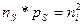. Поэтому увеличение концентрации электронов вблизи поверхности сопровождается уменьшением концентрации дырок. Анало­гичным образом образуется обогащенный дырочный приповерхностный слой при наличии на поверхности дырочного полупроводника отрицательного поверхност­ного заряда.

Если на поверхности электронного полупроводника преобладают акцепторные уровни, то она заряжается отрицательно. При этом электроны выталкиваются с поверхности вглубь кристалла, в результате чего образуется обедненный элект­ронами приповерхностный слой, концентрация электронов в котором ниже, чем в объеме полупроводника (рис. 1.59, б), и границы энергетических зон изгибают­ся вверх. При очень высокой плотности акцепторных уровней на поверхности электронного полупроводника может возникнуть инверсный дырочный слой, кон­центрация дырок в котором выше концентрации электронов (рис. 1.59, в). Анало­гичный процесс происходит на поверхности дырочного полупроводника при вы­сокой концентрации донорных уровней.

Наличие дефектов кристаллической структуры ведет к появлению вблизи сере­дины запрещенной зоны энергетических уровней, через которые происходит рекомбинация носителей заряда. Таких рекомбинационных центров на поверх­ности полупроводника больше, чем в объеме, поэтому скорость поверхностной ре­комбинации больше скорости объемной рекомбинации. При малых размерах кри­сталла поверхностная рекомбинация существенно уменьшает эффективное время жизни носителей заряда, определяемое по формуле

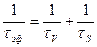
где 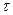_V— время жизни в объеме полупроводника;

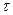_s — время жизни на поверхности полупроводника.

Плотность поверхностных состояний может изменяться с течением времени из-за испарения или конденсации влаги на поверхности кристалла, возможных миграций адсорбированных примесей на поверхности и т. п. Эти процессы, при­водящие к изменению эффективного времени жизни носителей зарядов, могут являться причиной нестабильности параметров и характеристик полупроводни­ковых приборов.