Рекомендуемая литература
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 2 (§ 2.6), гл. 8 (§ 8.9).
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 11 (§ 11.4, 11.5).
Основные определения
Статически определимая рама – конструкция, состоящая из нескольких изгибаемых стержней, закрепленных так, что опорные реакции и внутренние усилия можно найти с помощью уравнений статики. Чаще всего стержни рамы соединены между собой жестким образом, так, что в процессе деформации угол между стержнями не меняется. Мы будем рассматривать только плоские рамы, стержни которых расположены под углом 90°. Вертикальные стержни рамы принято называть стойками, горизонтальные – ригелями. В стержнях плоских рам возникают три внутренних усилия: продольная и поперечная силы и изгибающий момент.
Внутренние усилия в рамах определяются методом сечений, и порядок их нахождения тот же, что и для балок. Напомним, что согласно методу сечений:
·* продольная сила N равна сумме проекций всех сил, действующих с одной стороны от сечения, на ось стержня;
·* поперечная сила Q равна сумме проекций всех сил, действующих с одной стороны от сечения, на ось, перпендикулярную оси стержня;
·* изгибающий момент M равен сумме моментов всех сил, действующих с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения.
Правила знаков для продольной и поперечной сил те же, что и раньше: растягивающая продольная сила положительна, поперечная сила положительна, если она обходит сечение по ходу часовой стрелки. Правило знаков для изгибающего момента в рамах следующее: момент считается положительным, если он изгибает стержень рамы выпуклостью вовнутрь[10]. На эпюрах N и Q положительные значения принято откладывать снаружи, на эпюре М – внутри – со стороны растянутых волокон.
От действия трех внутренних усилий в стержнях рамы возникают напряжения: нормальные и касательные. Нормальные напряжения определяются как сумма напряжений от продольной силы (
) и от изгибающего момента по формуле (4.1). Касательные напряжения находят по формуле Журавского (4.2).
Перемещения точек оси рамы определяются, как правило, методом Максвелла – Мора по формуле (4.21). Заметим, что произвольная точка оси рамы в отличие от точки оси балки может перемещаться не только по вертикали, но и по горизонтали. Будем обозначать линейные перемещения точек оси рамы буквой d, отмечая направление перемещения индексом сверху: dверти dгор. Углы поворота сечений рамы, как и балок, обозначаем буквой j.
Примеры решения задач
Определение внутренних усилий в рамах
(задачи № 21, 22)
Условие задачи
Рассмотрим раму, показанную на рис. 4.26, и определим в ней внутренние усилия, то есть построим эпюры N, Q и М.
Решение
Найдем три опорные реакции, используя три уравнения статики. Желательно составлять такие уравнения, чтобы в каждое из них входила бы только одна неизвестная реакция. В данном примере это такие уравнения (предполагаемые направления реакций показаны на рис. 4.27, а):
Рис. 4.26. Схема рамы
с нагрузками
|
; 
; 
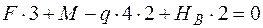кН;
проекций сил на вертикальную ось равна 0; 
; 
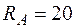кН;
; 
; 
кН.
Для проверки используем уравнение "сумма проекций сил на горизонталь- ную ось равна нулю":
.
Рис. 4.27. Определение внутренних усилий в раме:
а – схема рамы с нагрузками; б, в, г – эпюры внутренних усилий
|
Находим внутренние усилия, используя метод сечений. Рама имеет три участка. Заметим, что если для балки границей между участками считалось сечение, где появлялся новый силовой фактор, то для рам границей между участками является также и узел, где соединяются соседние стержни рамы (стойка и ригель). Рассечем стержни рамы на трех участках и выберем начало отсчета х на каждом участке (удобно начало отсчета выбирать в начале участка – рис. 4.27, а). Запишем выражения для продольной, поперечной сил и изгибающего момента на каждом участке, используя вышеприведенные определения этих усилий и правила знаков для них:
участок 1: 
м;
кН;
;
;
участок 2: 
м;
кН;
кН;
;
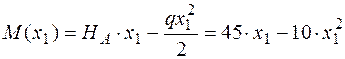участок 3: 
м;
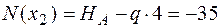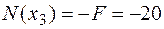кН;
кН;
.
Строим эпюры усилий, используя написанные выражения (рис. 4.27, б, в, г). Значение максимального момента определяем так же, как в балках.
Рис. 4.28. Проверка равновесия узлов
|
Проверку правильности построения эпюр в рамах производим, проверяя равновесие узлов. Для этого вырезаем узлы (в рассматриваемой раме их два: D и E) и прикладываем к сечениям, примыкающим к узлам, все внутренние усилия согласно построенным эпюрам. Направление усилий должно соответствовать их знакам. На рис. 4.28 показаны вырезанные из рамы узлы D и E вместе с действующими в сечениях, примыкающих к узлам, внутренними усилиями. Видно, что узлы находятся в равновесии. Из условия равновесия узлов следует, что, если в узле не приложена внешняя пара сил (узел D), то изгибающие моменты в сечениях, примыкающих к узлу, обязательно одинаковы. То есть, зная изгибающий момент в угловой точке для стойки, можно получить графически ординату М в угловой точке для ригеля, проведя циркулем дугу из вершины угла, как из центра. Если в узле действует сосредоточенная пара сил, то значения изгибающих моментов в примыкающих сечениях отличаются на величину этой пары.
4.2.2. Определение перемещений в рамах (задачи № 21, 22)
Условие задачи
Для рамы, показанной на рис. 4.26, найдем вертикальное перемещение точки В и угол поворота сечения А. Жесткость стержней рамы будем считать одинаковой (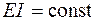
). Перемещения ищем методом Максвелла – Мора, интегрируя формулу Максвелла – Мора аналитически и графически (с помощью правила Верещагина).
Решение
Рис. 4.29. Рама под действием единичной обобщенной силы:
а – соответствующей  ; б – соответствующей 
|
Будем искать первое обобщенное перемещение – вертикальное перемещение точки В. В соответствии с методом Максвелла – Мора для определения этого перемещения приложим в точке В единичную вертикальную сосредоточенную силу (рис. 4.29, а) и найдем изгибающий момент, вызванный этой нагрузкой (координаты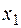 
, 
, 
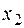должны отсчитываться так же, как при определении момента от заданной нагрузки):
участок 1: м;
;
участок 2: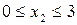 
м;
;
участок 3: 
м;
.
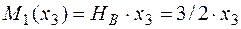Аналогично для определения второго обобщенного перемещения – угла поворота сечения А – приложим в точке А сосредоточенную пару сил, равную единице (рис. 4.29, б), и определим изгибающий момент от этой пары:
участок 1: м;
;
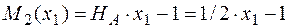участок 2: 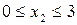м;
;
участок 3: 
м;
.
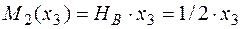Вариант 1. Аналитическое интегрирование формулы
Максвелла – Мора
Подставим в формулу Максвелла – Мора (4.21) выражения для изгибающих моментов от заданной нагрузки, найденные ранее при определении внутренних усилий в рассматриваемой раме, умножим их на выражения для изгибающих моментов от единичных обобщенных сил на всех трех участках и выполним интегрирование. Тогда, учтя, что 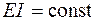, проинтегрируем формулу (4.21):
250 кН·м3;
–63,3 кН·м2.
В соответствии с правилом знаков метода Максвелла – Мора положительный знак вертикального перемещения говорит о том, что точка В перемещается по направлению обобщенной силы, то есть вверх. Сечение А поворачивается по часовой стрелке (в сторону, противоположную направлению единичной пары сил, так как знак угла поворота отрицательный).
Вариант 2. Интегрирование формулы Максвелла – Мора с помощью правила Верещагина
Рис. 4.30. Эпюры моментов: а – от заданной нагрузки;
б – от единичной обобщенной силы, соответствующей  ;
в – от единичной обобщенной силы, соответствующей 
|
Построим эпюры моментов от заданной нагрузки М и от единичных обобщенных сил, соответствующих искомым перемещениям, М 1 и М 2 (рис. 4.30). Для перемножения эпюр разобьем эпюру М на 4 простые фигуры: два треугольника w1 и w3, сегмент w2 и трапецию w4. Найдем ординаты под центрами тяжести этих фигур на эпюре М 1 (h1, h2 и h3 на рис. 4.30, б). Эпюру М на ригеле, имеющую форму трапеции w4 с основаниями разного знака, умножаем на трапецию эпюры М 1 по правилу трапеций (4.24). Согласно правилу Верещагина
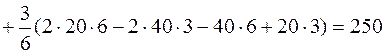кН·м3.
Аналогично находим угол поворота сечения А, перемножая эпюры М и М 2. Ординаты под центрами тяжести площадей w1, w2 и w3 показаны на рис. 4.30, в (h¢1, h¢2 и h¢3). Для перемножения трапеции w4 на прямоугольник эпюры М 2 нет необходимости пользоваться правилом трапеций, так как, где бы ни находился центр тяжести трапеции, значение h¢4 известно (ординаты на эпюре М 2 на этом участке постоянны).
Рис. 4.31. Изогнутая ось рамы
|
кН·м2.
Результаты, полученные по двум вариантам использования формулы Максвелла – Мора, совпадают.
В заключение построим деформированную ось рамы так, чтобы она удовлетворяла эпюре изгибающих моментов и условиям закрепления рамы (рис. 4.31). На рис. 4.31 показаны полученные перемещения – , в соответствии с их направлениями. Точка перегиба (крестик) изогнутой оси ригеля имеет место в сечении, где меняет знак изгибающий момент. Углы рамы в процессе деформации не меняются.[11]
