Лабораторная работа по теме. «Технология решения обыкновенных

«Технология решения обыкновенных

дифференциальных уравнений средствами MatLab»

 

 

Вопросы, подлежащие изучению

 

1) Нахождение символьного выражения производной от функции с использованием функции diff().

2) Вычисление числовых значений производных в точках.

3) Функции Matlab, предназначенные для решения ОДУ (ode23(), ode45()).

4) Вывод результатов решения ОДУ в виде таблицы.

5) Получение графического решения ОДУ.

 

 

Общее задание

 

1) Изучите материал Темы 2.4 (п. 2.4.1).

2) Выберите индивидуальный вариант задания из табл. 2.4.2-1.

3) Найдите символьное выражение производной от функции f(x) и вычислите значение производной от функции f(x) в произвольной точке с.

4) Найдите решение ОДУ на отрезке [a;b] с шагом h с использованием функций ode23() и ode45().

5) Создайте матрицу решений, записав в первый столбец аргумент, во второй и третий - решение, полученное с использованием функций ode23() и ode45(), а в четвертый столбец – погрешность метода (модуль разности решений ОДУ с использованием функций ode23() и ode45()).

6) Выведите полученную таблицу по столбцам.

7) Постройте графики полученных решений ОДУ в одном шаблоне.

8) Сохраните текст рабочего окна на внешнем носителе.

9) Представьте результаты работы преподавателю, ответьте на поставленные вопросы.

10) Выполните команду clear all.

11) Оформите отчет по выполненной работе.

Варианты индивидуальных заданий

Таблица 2.4.2-1

 

№	f(x)	ОДУ	Начальные условия	b	h
				0,5	0,5
				1.2
				0.4
					0,5
				0.4	0,2
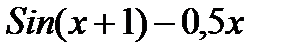
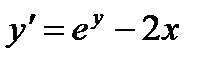
				0.2	0,2
				0.5	0,25
				0,25
					0,5
				0,3	0,15
				0,5	0,25
				0,5	0.5
					0,5
					0,5
					0,5
					0,5
					0,5
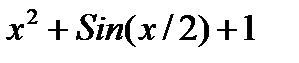
					0,5
					0,25
					0,5
				1,5	0,5
				1.4
					0,5
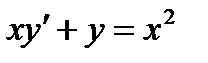
					0,5
					0,5
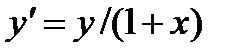
				1,4	0,2
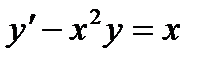
				1,4	0,2
					0.5

Содержание отчета

 

1) В форме комментариев:

· Название лабораторной работы

· ФИО студента, номер группы

· № варианта

· Индивидуальное задание

2) Протокол вычислений (сессии) в окне Command Window, снабженный необходимыми комментариями.

 

Контрольные вопросы по теме

1) Какие начальные условия должны быть заданы в соответствии с задачей Коши при решении ОДУ средствами системы Matlab?

2) Какие численные методы реализованы в функциях Matlab ode23() и ode45()?

3) Что является входными параметрами функций ode23() и ode45()?

4) В какой форме должны быть записаны функции ОДУ при использовании ode23() и ode45()?

5) Можно ли задать при решении ОДУ средствами Matlab требуемую точность вычислений?

6) Что представляет собой решение ОДУ второго порядка при использовании функций ode23() и ode45()?

7) Почему при решении ОДУ старших порядков необходимо использовать векторную функцию?

 

 

8)

Тема 2.5. Технология решения задач одномерной оптимизации

2.5.1. Решение задач одномерной оптимизации функций

2.5.2. Лабораторная работа по теме «Технология решения задач

одномерной оптимизации»

2.5.3. Контрольные вопросы по теме