выполнить сплайн-интерполяцию с использованием полиномов нулевой, первой и третьей степени, и получить значения функции в точке х=0.58.
|
Рис. 2.2.1-5. Вычисление функции в точке х=0.58
На рис. 2.2.1-6 и 2.2.1-7 приведены команды, необходимые для проведения интерполяции таблично заданной функции и построения графиков интерполируемой функции и интерполирующих ее интерполяционных многочленов различных степеней.
|
Рис. 2.2.2-6. Команды построения графиков интерполяционных функций
Рис. 2.2.2-7. Графики интерполирующих функций
Лабораторная работа по теме
«Технология аппроксимации интерполяции функций»
Вопросы, подлежащие изучению
1) Задание векторов и матриц в пакете Matlab.
2) Технология аппроксимации функции, заданной таблично, с использованием функций polyfit ().
3) Технология линейной, кубической и сплайн-интерполяции таблично заданной функции с использованием функций interp1().
4) Получение интерполяционных многочленов в явном виде.
5) Построение графиков аппроксимирующих и интерполирующих функций.
Общее задание
1) Изучите материал Темы 2.2. (п. 2.2.1).
2) Выберите индивидуальное задание: номера узлов и номер аппроксимируемой функции из табл. 2.2.2-1; узлы аппроксимации и значения функции в узлах из табл. 2.2.2-2.
3) Задайте в виде векторов значения узлов и значения функции в выбранных узлах.
4) Вычислите коэффициенты аппроксимирующих функций для линейной, квадратичной и кубической аппроксимации с использованием функции polyfit() и получите три аппроксимирующие функции в явном виде.
5) Получите с использованием этих функций значение аппроксимирующей функции в произвольной точке, принадлежащей отрезку, но не совпадающей с узлами аппроксимации, и сравните полученные результаты.
6) Постройте графики табличной и трех аппроксимирующих функций в одном шаблоне, снабдив их легендой.
7) Проведите линейную и кубическую интерполяцию функции с использованием функции interp1(), заданной таблично. Получив значения интерполирующей функции в точке, не совпадающей с узлами интерполяции, сравните полученные результаты.
8) Постройте графики табличной и двух интерполирующих функций в одном шаблоне, снабдив их легендой.
9) Представьте результаты работы преподавателю, ответьте на поставленные вопросы.
10) Выполните команду clear all.
11) Оформите отчет по выполненной работе.
3. Варианты заданий
Таблица 2.2.2-1
| Вариант № | Номера узлов xi | Номер функции |
| 1 3 5 7 9 10 13 | 
| |
| 1 2 4 5 7 10 12 | 
| |
| 1 3 6 7 10 11 13 |
| |
| 1 2 4 7 9 11 13 |
| |
| 3 6 7 9 10 11 12 |
| |
| 2 3 6 8 9 10 13 |
| |
| 1 4 5 7 9 11 12 |
| |
| 1 2 4 7 9 12 13 |
| |
| 2 3 5 7 8 11 12 |
| |
| 1 3 6 7 9 10 13 | 
| |
| 1 3 7 8 10 11 13 | 
| |
| 1 2 5 6 7 10 12 | 
| |
| 1 4 5 8 10 12 13 | 
| |
| 1 3 5 7 9 10 13 | 
| |
| 1 3 6 7 8 10 13 | 
| |
| 1 4 5 7 9 11 12 | 
| |
| 2 4 5 6 8 12 13 | 
| |
| 1 4 5 7 9 11 12 |
| |
| 1 4 5 8 10 11 12 |
| |
| 2 4 5 6 8 12 13 |
| |
| 1 4 5 8 10 12 13 | 
| |
| 2 3 6 8 9 10 13 | 
| |
| 1 3 5 8 10 12 13 | 
| |
| 1 4 5 7 9 11 12 | 
| |
| 2 4 5 6 8 12 13 | 
| |
| 3 4 5 7 8 9 12 | 
| |
| 3 5 8 10 11 12 13 |
| |
| 2 4 7 9 10 11 13 |
| |
| 2 4 5 7 8 10 12 |
| |
| 1 4 5 7 9 11 13 |
|
Таблица 2.2.2-2
| i | xi | 
| 
| 
|
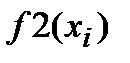
| -5 | 1.38 | 2.44 | 1.676 | |
| -4.5 | 1.221 | 2.359 | 2.025 | |
| -4 | 1.511 | 1.751 | 1.736 | |
| -3.5 | 1.501 | 2.13 | 1.203 | |
| -3 | 1.455 | 1.511 | ||
| -2.5 | 0.728 | 1.482 | 1.362 | |
| -2 | 0.976 | 1.437 | 0.75 | |
| -1.5 | 1.065 | 0.803 | 0.976 | |
| -1 | 0.599 | 1.175 | 0.957 | |
| -0.5 | 0.192 | 0.49 | 0.272 | |
| 0.3 | 0.375 | 0.3 | ||
| 0.5 | 0.319 | -6.51*10-3 | 0.165 | |
| -0.405 | -1.965 | -1.185 |
Содержание отчета
1) В форме комментариев:
· Название лабораторной работы
· ФИО студента, номер группы
· № варианта
· Индивидуальное задание
2) Протокол вычислений (сессии) в окне Command Window, снабженный необходимыми комментариями.
Контрольные вопросы по теме
1) Что такое аппроксимация функции и в каких случаях она используется?
2) В чем отличие аппроксимации от интерполяции?
3) Какой метод аппроксимации реализован в функции polyfit()?
4) Что служит результатом выполнения функции polyfit()?
5) Для чего предназначена функция polyval()?
6) Назначение и формат функции interp1()?
7) Каким параметром определяется тип интерполяции в функции interp1()?
Тема 2.3. Технология интегрирования
в среде MatLab
2.3.1. Вычисление неопределенных и определенных интегралов
2.3.2. Лабораторная работа по теме «Технология интегрирования
в среде MatLab»
2.3.3. Контрольные вопросы по теме
2.3.1. Вычисление неопределенных и
определенных интегралов
При вычислении определенных интегралов первообразную функцию F(x) не всегда удается выразить аналитически, а кроме того иногда подынтегральная функция f(x) задана в виде таблицы (xi и yi, где i = 1, 2, …, n). Это приводит к необходимости использования численных методов интегрирования.
Существует ряд методов численного интегрирования. Во всех этих методах вычисление осуществляется по приближенным формулам, называемым квадратурами.
Суть получения формул численного интегрирования состоит в том, что на элементарных отрезках интегрирования подынтегральную функцию заменяют простейшим интерполяционным полиномом, который легко может быть проинтегрирован в аналитическом виде. Так, например, для получения формул прямоугольников, трапеций и Симпсона используют полиномы соответственно нулевой, первой и второй степени.
Формулы прямоугольников:
где:
h – шаг интегрирования;
yi – значение подынтегральной функции от аргумента xi, k=0, 1, …,n;
n – число разбиений интервала интегрирования a, b.
Формула трапеций:
где:
h – шаг интегрирования;
y0 – значение подынтегральной функции при х = a;
yn – значение подынтегральной функции при х = b;
Формула Симпсона:
Для символьного вычисления неопределенных и определенных интегралов используется функция Matlab int(), которая может иметь один из следующих форматов:
· int(S) – возвращает символьное значение неопределенного интеграла от символьного выражения или массива символьных выражений S по переменной, которая автоматически определяется функцией findsym(). Если S – скаляр или матрица, то вычисляется интеграл по переменной 'х'.
· int(S, v) – возвращает неопределенный интеграл от S по символьной переменной v.
· int(S, a, b) – возвращает определенный интеграл от S с пределами интегрирования от а до b, причем пределы интегрирования могут быть как символьными, так и числовыми.
· int(S, v, a, b) – возвращает определенный интеграл от S по переменной v с пределами от а до b.
Ниже приведены примеры использования функции Matlab int()
(рис. 2.3.1-1).
|
Рис. 2.3.1-1. Примеры вычисления интегралов
В системе MatLab функции вычисления интегралов используют численные методы трапеции, Симпсона и некоторые другие. Рассмотрим технологию интегрирования с использованием некоторых функций.
Для вычисления интеграла по формуле трапеции в MatLab используется функция trapz(x,y). Эта функция возвращает значение интеграла 
от функции y(x), которая может быть представлена вектором или матрицей. Если y(x) – матрица, то функция возвращает вектор значений интеграла каждого столбца матрицы. Если вектор узлов не задан - trapz(y), то в качестве ординат x используются индексы вектора y (x=1:length(y)), где функция определяет длину вектора y. Важно, что узлы по оси x могут быть как равноотстоящими, так и неравноотстоящими.
Рассмотрим несколько примеров вычисления значений определенных интегралов методом трапеций при различных способах задания узлов подынтегральной функции (рис. 2.3.1-2).
|
Рис. 2.3.1-2. Вычисление определенных интегралов с использованием
ФункцииMatlab trapz()
Для вычисления интеграла по формуле Симпсона в MatLab применяется функция quad(). При обращении к этой функции шаг интегрирования не задается, а используется параметр – требуемая точность вычисления интеграла.
Минимальная форма обращения к функции – q=quad('f',a,b), где f – имя функции, взятое в одинарные кавычки, второй и третий аргументы – пределы интегрирования.
|
Рис. 2.3.1-3. Вычисление определенных интегралов
с использованием функции quad()
Допускается задание четвертого входного параметра eps – абсолютной погрешности: q=quad('f', a, b, eps ). По умолчанию eps =10-6.
Рассмотрим примеры вычисления определенного интеграла 
с использованием функции Matlab quad() (рис. 2.3.1-3).
