«Технология интегрирования в среде Matlab»
Вопросы, подлежащие изучению
1) Получение символьного выражения неопределенного интеграла средствами пакета Matlab.
2) Вычисление значения определенного интеграла с использованием функций.
3) Вычисление значения определенного интеграла с использованием функций Matlab int(), trapz(), quad().
4) Формулы численного интегрирования: средних прямоугольников, трапеций и Симпсона.
Общее задание
1) Изучите материал Темы 2.3 (п. 2.3.1).
2) Выберите из табл. 2.3.2-1 вариант индивидуального задания.
3) Получить символьное выражение неопределенного интеграла с использованием функций int( S) и int( S, x ), где S – символьное выражение, а х - переменная.
4) Вычислите значение определенного интеграла с использованием функции int() формата int( S,a,b ), где a, b – пределы интегрирования.
5) Вычислите определенный интеграл с использованием функции Matlab, реализующей формулу трапеций, - trapz(x, y), предварительно получив таблицу значений подынтегральной функции с шагом h и задав значения аргумента и функции в виде векторов.
6) Вычислите значение определенного интеграла с использованием функции Matlab, реализующей формулу Симпсона, – quad('f',a,b), где f – имя функции, взятое в одинарные кавычки.
7) Представьте результаты работы преподавателю, ответьте на поставленные вопросы.
8) Выполните команду clear all.
9) Оформите отчет по выполненной работе.
Варианты индивидуальных заданий
Таблица 2.3.2-1
| № | Интеграл 1 | Интеграл 2 |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
|
Содержание отчета
1) В форме комментариев:
· Название лабораторной работы
· ФИО студента, номер группы
· № варианта
· Индивидуальное задание
2) Протокол вычислений (сессии) в окне Command Window, снабженный необходимыми комментариями.
Контрольные вопросы по теме
1) Какой функцией в Matlab определяется символьное значение определенного интеграла?
2) Назначение функции trap(x,y).
3) Что возвращает функция trap(x,y), если y(x) – матрица?
4) Можно ли использовать функцию trap(x,y), если узлы по оси х - не равноотстоящие?
5) Какая функция Matlab позволяет вычислить определенный интеграл с заданной точностью?
6) Способы задания подынтегральной функции при вычислении определенного интеграла с использованием функции quad().
7) Какова точность вычисления определенного интеграла по умолчанию?
Тема 2.4. Технология решения обыкновенных
дифференциальных уравнений
2.4.1. Численное решение обыкновенных дифференциальных уравнений
2.4.2. Лабораторная работа по теме
2.4.3. Контрольные вопросы по теме
2.4.1. Численное решение обыкновенных
дифференциальных уравнений
Представим обыкновенное дифференциальное уравнение (ОДУ) первого порядка в виде, разрешенном относительно производной 
, и пусть 
– начальные условия его решения.
Тогда решением ОДУ является функция 
, которая, будучи подставленной в исходное уравнение, обратит его в тождество, и одновременно будут выполняться начальные условия. Эта задача в математике называется задачей Коши.
Задача Коши при решении ОДУ n-го порядка 
формулируется аналогично, при этом начальными условиями должны быть: 
При решении ОДУ n-го порядка уравнение путем выполнения ряда обозначений 
представляется в виде системы дифференциальных уравнений:
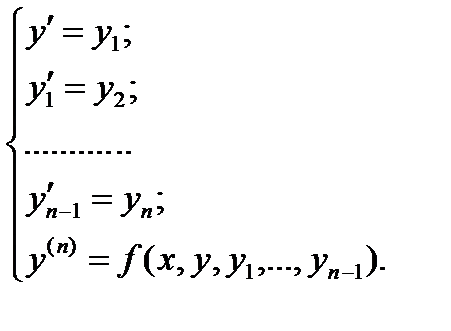
Результатом решения ОДУ численными методами является таблица значений y = j(x) на некотором множестве значений аргументов. Поэтому при постановке задачи численного решения ОДУ наряду с начальными условиями x0, y0 необходимо задать область решения – отрезок [a;b] и шаг изменения аргумента h (шаг интегрирования).
Для получения численного решения ОДУ используются методы Рунге-Кутты [1]. Методы различаются порядком. Чем выше порядок метода, тем точнее решение, полученное при равном шаге интегрирования.
В Matlab имеется несколько функций для решения задачи Коши. Рассмотрим две функции, используемые для решения обыкновенных дифференциальных уравнений (ОДУ): ode23() – использует метод Рунге-Кутты второго и третьего порядка; ode45() – использует метод Рунге-Кутты четвёртого и пятого порядка точности с автоматическим выбором шага.
В MatLab обращением к функциям, предназначенным для решения ОДУ, является:
[x, y] = ode23('fun',t0,tf,x0)
[x, y] = ode45('fun',t0,tf,x0)
Входными параметрами функций являются:
· 'fun' – имя функции (в виде строчной переменной) или ссылка на функцию, задающую правую часть дифференциального уравнения (уравнение должно быть записано в нормальной форме
y' = fun(x,y));
· t0 – начальное значение аргумента;
· tf – конечное значение аргумента;
· х0 – вектор начальных условий.
Выходными параметрами функций являются:
· x – вектор, содержащий отсчёты аргумента в точках решения;
· y – вектор, содержащий вычисленные значения результата решения ОДУ в точках, соответствующих отсчетам независимой перемен-ной x.
Требования к точности и другие параметры численного решения задаются в Matlab по умолчанию. Изменить эти настройки позволяет дополнительный аргумент OPTIONS.
|
Рис. 2.4.1-1. Решение ОДУ методом Рунге-Кутты второго порядка
Рассмотрим примеры использования функций ode23() и ode45() для решения ОДУ вида: 
на отрезке [1;10] с шагом интегрирования 1 при начальных условиях y(1)=1. Решение ОДУ с использованием функции ode23() приведено на рис. 2.4.1-1.
На рис. 2.4.1-2 приведено решение того же ОДУ, но с использованием функции ode45(). Вывод таблицы решения дополнен графиком функции y(x) (рис. 2.4.1-3).
|
Рис. 2.4.1-2. Решение ОДУ методом Рунге-Кутты четвертого порядка
Рис. 2.4.1-3. Графическое решение ОДУ
При решении ОДУ высокого порядка вводят обозначения (новые функции) для всех производных, кроме самой старшей. В этих обозначениях самая старшая производная становится записанной, как первая. Исходное уравнение дополняется тождествами, определяющими правила введения новых функций. Проиллюстрируем описанный подход при решении ОДУ второго порядка.
Требуется решить 
с начальными условиями: и 
. Сведем заданное ОДУ к равноценной системе ОДУ первого порядка. Для этого переобозначим функцию 
, как 
, и введем функцию 
. Запишем исходное уравнение в новых обозначениях: 
(здесь учтено, что 
). Дополним это уравнение тождеством 
и получим нужную систему ОДУ. Эту систему следует дополнить начальными условиями: 
Решение системы ОДУ в Matlab начинается с определения векторной функции (рис. 2.4.1-4).
Рис. 2.4.1-4. Определение векторной функции
Для решения дифференциального уравнения (системы уравнений) используем команды, где решение системы ОДУ записывается в переменную y. При этом элемент y(1) содержит значение функции y(x), а y(2) значение производной y'(x). Команда plot(x, y) строит график функции решения ОДУ и ее производной (рис. 2.4.1-6).
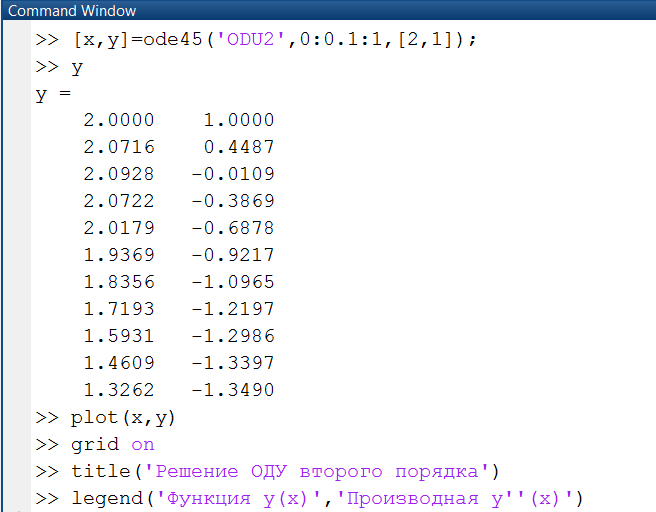
Рис. 2.4.1-5. Решение ОДУ второго порядка
Рис. 2.4.1-6. Графики функций решения ОДУ и производной
