Загальні положення
Фізика – наука експериментальна, а тому на першому плані під час її вивчення – фізичний практикум.
В даній роботі пропонується комп’ютерний практикум, який включає віртуальні лабораторні роботи з усіх основних розділів і тем курсу фізики та дозволяє після його виконання отримати міцні знання з основних явищ і законів фізики та скласти загальну уяву про предмет фізики.
Методичні вказівки до кожної роботи містять: основні теоретичні відомості про явища, які вивчаються; основні фізичні закони, що їх описують; стислий опис алгоритму комп’ютерної програми та її можливостей; вказівки до виконання роботи; вказівки щодо змісту звіту; запитання та завдання для самоконтролю.
Лабораторні роботи виконуються відповідно до семестрового графіка, який знаходиться на стенді в лабораторії, тому кожен студент має можливість підготуватися до них заздалегідь.
Виконання лабораторного завдання складається з попередньої підготовки, проведення комп'ютерного експерименту і складання звіту про результати роботи. До виконання лабораторної роботи необхідно готуватись заздалегідь, вивчити конспект лекцій і рекомендовані розділи навчальних посібників [1...6].
Допуск до виконання лабораторної роботи проводиться викладачем перед початком роботи опитуванням (письмово чи усно) тільки за наявності повністю оформленого звіту за попередньою роботою і підготовленого звіту до роботи, яка виконуватиметься. В комп’ютерному класі проводяться тільки комп’ютерний експеримент і розрахунки.
Після проведення комп’ютерного експерименту результаті розрахунків необхідно показати викладачеві, а до кінця заняття написати звіт з виконаної роботи.
Звіт з лабораторної роботи оформлюється згідно з ДСТУ 3.008-95 [7]. Захист оформлених звітів проводять у вигляді здачі циклу лабораторних робіт
(3-4 роботи) на підсумковому занятті згідно з графіком.
До здачі циклу допускають студентів, які виконали лабораторні роботи й оформили звіт. Захист робіт проводиться в формі опитування за змістом виконаних лабораторних робіт. Перелік контрольних запитань та завдань наведений у кінці опису кожної роботи.
В роботі через технічні причини деякі рисунки подані російською мовою.
ЧАСТИНА I. ФІЗИЧНІ ОСНОВИ МЕХАНІКИ
Вивчення вільного падіння
1.1 Мета роботи
Вивчити закономірності вільного падіння тіл в полі тяжіння, визначити прискорення вільного падіння. Ознайомитись з методом обчислення похибок прямих та непрямих вимірювань.
1.2 Вказівки з організації самостійної роботи студентів
Прискорення вільного падіння – це прискорення, якого набуває тіло під час руху в полі сили тяжіння. Поблизу поверхні Землі сила тяжіння залежить від географічної широти місцевості та висоти над рівнем моря. Зі збільшенням висоти над поверхнею Землі сила тяжіння зменшується обернено пропорційно квадрату відстані між центрами тіла та Землі.
В даній роботі прискорення вільного падіння g визначається за прямими вимірюваннями часу t та висоти падіння h. Відстань H, яку тіло проходить за час t, визначається за кінематичним законом руху
, (1.1)
звідки 
, або 
. (1.2)
Якщо виміряти час падіння кульки з різної висоти та побудувати графік залежності 
від t, то згідно з (1.2) отримаємо пряму, тангенс кута нахилу якої до осі t дорівнюватиме 
.
Графік залежності від t (рис.1.1) дає можливість обчислити значення g за формулою
. (1.3)
1.3 Опис комп’ютерної програми
Зовнішній вигляд інтерфейсу програми зображено на рис. 1.2. Програма моделює рух тіла в середовищі в широких межах зміни густини середовища 
та коефіцієнта в’язкості, а також в частинному випадку, коли 
, 
, тобто, у вакуумі. Одновимірний рух тіла (кульки) описується за допомогою модифікованого метода Ейлера (додаток Б) з урахуванням сил, які діють на кульку (з якими ви детально ознайомитесь під час виконання роботи 1.2). Шлях падіння кульки вимірюється за шкалою, на якій нанесені поділки в м. Час падіння кульки вимірюється секундоміром. На екрані дисплею виведені кнопки регулювання секундоміра для вмикання, вимикання та скидання до нуля. Програма дозволяє зупинити процес падіння в будь-який момент, а потім або продовжити зі збереженими значеннями величин на цей момент часу, або повернутися до початкового моменту.
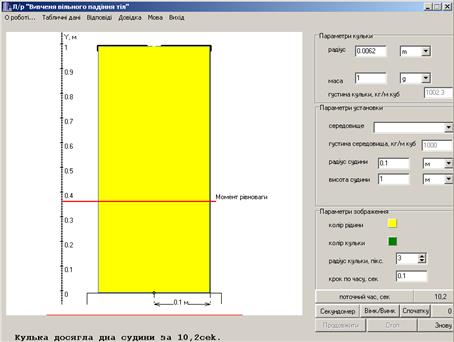
Рисунок 1.2
1.4 Інструкція користувачу
1. Встановити у вікні інтерфейсу “рідина N” – “інша”. Задати значення густини 
кг/м3, в’язкості 
Па×с. Обнулити показання секундоміра, натиснувши на “Знову”.
2. Встановити висоту посудини Н,масу кульки m та її радіус R згідно з номером варіанта з табл. 1.1. Одразу після запуску програми, ввімкніть секундомір. В момент досягнення кулькою дна посудини, вимкнути секундомір. Занести в табл. 1.2 значення висоти та часу падіння. Повторити вимірювання 3...5 разів для кожного з шести значень висоти падіння Н. Висоту падіння кожного разу збільшувати, починаючи з початкового значення наведеного в табл. 1.1, на 2 м. Занесіть дані в табл. 1.2.
Обчислити середнє значення 
для кожного значення висоти.
Таблиця 1.1 – Вихідні дані
| Номер вар. | ||||||||||||
| R, м | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 |
| H, м | ||||||||||||
| m, г |
3. Побудувати графік залежності від 
. Обчислити величину g за формулою (1.3).
4. Обчислити похибки вимірювань.
5. Провести експеримент пункту 2 для випадку, коли кулька падає в реальних умовах – у повітрі. Для цього задати значення густини середовища 
кг/м3, коефіцієнта в’язкості 
Па×с. Результати занести в таблицю, подібну до табл. 1.2. Побудувати залежність від t на тому самому графіку, що й для вакууму. Обчислити величину g за формулою (1.3).
6. Обчислити похибки вимірювань прискорення вільного падіння.
Таблиця 1.2 – Результати розрахунків
| Номер експерименту | Час падіння, с | |||||
| t1 | t2 | t3 | t4 | t5 | t6 | |
| Середнє значення t |
1.5 Зміст звіту
Звіт має містити: мету роботи; дані вимірювань, занесені до таблиці; залежності від t для вакууму та повітря, наведені на одному рисунку; висновки з результатів порівняння графіків; результати обчислення похибок вимірювання; результат обчислення прискорення вільного падіння у вигляді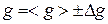 
(у вакуумі та повітрі, порівняння величини g з табличним значенням для даної широти місцевості).
1.6 Контрольні запитання і завдання
1. Назвіть мету даної роботи.
2. Як залежить величина прискорення вільного падіння від географічної широти місцевості та висоти над рівнем моря?
3. Яким кінематичним законом описується вільне падіння тіл?
4. Запишіть формулу, за якою визначається прискорення вільного падіння в даній роботі.
5. Які вимірювання називають прямими?
6. Які вимірювання називають непрямими?
7. Як обчислюються похибки при прямих вимірюваннях?
8. Як обчислюються похибки при непрямих вимірюваннях?
Вивчення вільних коливань лінійного осцилятора
2.1 Мета роботи
Вивчити закономірності згасаючих коливань і визначити коефіцієнт згасання, логарифмічний декремент згасання та добротність.
2.2 Вказівки до організації самостійної роботи
Лінійним осцилятором називають тіло (матеріальну точку), яка здійснює гармонічні коливання.
В ідеальній коливальній системі, в якій відсутні сили опору, можуть існувати коливання зі сталою амплітудою. В такій системі у випадку малих значень амплітуди діє квазіпружна сила [1, 4]:
, (2.1)
де k – коефіцієнт пружності.
Рівняння руху матеріальної точки в цьому випадку має такий вигляд:
, (2.2)
де x″ – друга похідна від x за часом, m – маса тіла
. (2.3)
Такі коливання відбуваються з власною частотою
. (2.4)
В реальних коливальних системах завжди присутні сили опору, дія яких зменшує енергію системи.
Розглянемо вільні згасаючі коливання. Якщо швидкість руху невелика, сила опору середовища пропорційна швидкості
, (2.5)
де 
–похідна за часом.
Знак мінус вказує на те, що сила F спрямована проти напрямку руху. Запишемо рівняння руху
, (2.6)
де r – коефіцієнт опору.
Вводячи позначення 
, отримуємо рівняння
,(2.7)
де 
– коефіцієнт згасання коливань.
Це лінійне диференціальне рівняння другого порядку зі сталими коефіцієнтами. Якщо згасання незначне (
), розв’язок рівняння (2.7) має такий вигляд:
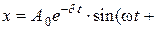
),(2.8)
де A 0 – амплітуда коливань в момент часу t = 0, – початкова фаза.
Згасаючі коливання не є періодичними, бо в них ніколи не повторюються максимальні значення зміщення, швидкості, прискорення.
Величину T називають періодом коливань (згасаючих коливань) внаслідок того, що коливальна система проходить положення рівноваги через рівні проміжки часу [1, 4]
. (2.9)
Амплітуда згасаючих коливань зменшується зі зміною часу за законом
. (2.10)
З формули (2.10) випливає
. (2.11)
Натуральний логарифм відношення амплітуд зміщень, які розрізняються в
часі на проміжок 
, називають логарифмічним декрементом згасання 
. (2.12)
2.3 Опис комп’ютерної програми
Зовнішній вигляд інтерфейсу програми зображено на рис. 2.1. Програма дає можливість вивчати незгасаючі коливання системи за різних умов їх збудження: шляхом відхилення пружинного маятника від положення рівноваги та шляхом надання йому певного значення початкової швидкості. Програма будує графіки залежності відхилення х від положення рівноваги як функцію часу в широких межах зміни параметрів початкового положення 
, початкової швидкості 
, значень маси тіла m, жорсткості пружини 
та величини коефіцієнта опору 
. Для завдання значень змінних параметрів , 
, , 
, виведено відповідні кнопки (рис.2.1) на інтерфейсі програми. Кнопки 
, 
призначені для регулювання початкового та кінцевого моменту зображення графіка коливань. Програма дозволяє вивчати як незгасаючі коливання, коли сили тертя відсутні (
), так і згасаючі коливання, коли 
, а також аперіодичний режим, тобто такий режим, коли тертя в системі досягає таких меж, що система, відхилена від положення рівноваги, повільно повертається до цього положення і коливання не виникають (
).
Рисунок 2.1
2.4 Інструкція користувачу
1. Прибрати галочку з . Встановити 
=0,0001 H, r =0 кг/с (δ=0), γ=0 (γ – стала величина, яка характеризує нелінійність повертаючої сили). Отримати незгасаючі коливання.
2. Забезпечити режим вільних коливань, прибравши галочку з 
і поклавши =0,001 H, r =0,2 кг/с. Початкові умови встановити у вигляді =0 м/с, 
=0,1 м. Зауваження:
1) якщо крива виходить не гладкою, а ламаною, то зменшити крок h;
2) якщо крива має дуже багато періодів, то зменшити параметр 
3. Отримати 
для параметрів m, r і , взятих з табл. 2.1. Заміряти кілька амплітуд (A 1, A 2, A 3, A 4) та відповідні їм моменти часу t. Визначити три значення логарифмічного декремента згасання λ та його середнє значення. Результати занести до табл. 2.2.
Таблиця 2.1 – Вихідні дані
| Номер вар. | , м
| r, кг/с | m, кг | Номер вар. | , м
| r, кг/с | m, кг |
| 0,1 | 0,1 | 0,1 | 0,1 | 0,1 | 0,2 | ||
| 0,1 | 0,2 | 0,1 | 0,1 | 0,2 | 0,2 | ||
| 0,1 | 0,3 | 0,1 | 0,1 | 0,3 | 0,2 | ||
| 0,2 | 0,1 | 0,1 | 0,2 | 0,1 | 0,2 | ||
| 0,2 | 0,2 | 0,1 | 0,2 | 0,2 | 0,2 | ||
| 0,2 | 0,3 | 0,1 | 0,2 | 0,3 | 0,2 |
4. Збільшуючи r, досягти аперіодичного режиму в двох випадках за початкових умов:
1) =0,1 м, =0;
2) =0, =0,5 м/с.
Таблиця 2.2 – Результати розрахунків
| Номер |  ,с
| А, м | № | λ | < λ > |
| 2 | |||||
5. Зарисувати для обох випадків графіки .
2.5 Зміст звіту
Звіт має містити: мету роботи, рисунок кривої при одному зі значень r; значення чотирьох амплітуд (A 1, A 2, A 3, A 4), обчислення трьох значень та середнього значення λ, графіки аперіодичного режиму для двох випадків початкових умов (п.5 завдання), висновки (повинні містити відповідь на запитання п.6).
2.6 Контрольні запитання і завдання
1. Який рух називається коливальним?
2. Що таке осцилятор?
3. Запишіть диференціальне рівняння незгасаючих коливань. Який вигляд має його розв’язок?
4. Запишіть диференціальне рівняння згасаючих коливань. Який вигляд має його розв’язок?
5. Який фізичний зміст має коефіцієнт згасання?
6. Що таке логарифмічний декремент згасання?
7. Отримайте формулу, яка пов’язує коефіцієнт згасання з декрементом.
