Инфляция – это обесценивание денег, обусловленное чрезмерным увеличением выпущенной в обращение массы бумажных денег и безналичных выплат по сравнению с реальным предложением платных товаров и услуг. Дефляция – обратный процесс – это изъятие из обращения части избыточной денежной массы, комплекс мер по сдерживанию или уменьшению инфляции. Процесс дефляции характерен для случая, когда экономика находится в состоянии глубокого кризиса.
До 1936 г. считалось, что инфляция исключительно деструктивна. Однако, по утверждению Дж. Кейнса, инфляция приводит к развитию экономики, безинфляционное развитие – к накоплению денег, между тем как инфляция обесценивает их и стимулирует потребление.
Основными показателями инфляции считаются: 1средний годовой уровень инфляции (α):
αг=ΔS/S,
где S – некоторая сумма денег, имеющаяся у клиента в данный момент; ΔS – некоторая сумма денег, которая добавляется к S для сохранения покупательной способности.
2) 2 индекс инфляции (Iи):
Iи= Sα/S,
где Sα – сумма денег через время t, покупательная способность которой равна S.
Так как Sα = S + ΔS, то Iи= 1+ αг и αг= Iи – 1.
С учетом инфляции, годовой уровень которой равен αг, FVα или Sα =PV(1+ 
).
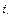- годовая процентная ставка, которая бы обеспечивала прибыль от наращения по годовой ставке 
и покрывала потери от инфляции.
= 
.
Наращенная сумма с учетом инфляции:
, где Кни= 
= 
.
Если срок кредита или депозита составляет t дней при годовой процентной ставке I и годовом уровне инфляции α, то величина наращенной суммы
FVα= 
= 
.
Сложные проценты и инфляция
Наращенная сумма по сложным процентам определяется по формуле
.
Ставка сложных процентов с учетом инфляции:
= 
.
Коэффициент наращения:
Кни= 
.
Если сложные проценты начисляются m раз в году и n лет по номинальной ставке сложных процентов j, то наращенная сумма с учетом инфляции равна
Sα= 
Денежный поток
Математические основы анализа инвестиционных проектов
Принимая решение об инвестировании денег в проект, необходимо учитывать возможность их альтернативного использования. Для определения будущего размера данной суммы используют формулу сложных процентов 
.
Из формулы сложных процентов можно вывести формулу для оценки текущей стоимости будущих поступлений 
Это действие (т.е. сведение будущих денежных сумм к настоящему моменту времени) называется дисконтированием. Оно показывает, какую сумму в размере Р денежных единиц необходимо сегодня положить на счет, чтобы через n лет с учетом сложных процентов ее величина составила F денежных единиц. Параметр r (i) называется ставкой дисконтирования.
Выражение 
называется финансовым множителем FM1(r,n).
Выражение 
- финансовым множителем FM2(r,n).
Таким образом, формулу сложных процентов можно представить в виде F=PFM1(r,n), а формулу дисконтирования - в виде P=FFM2(r,n).
