Если 
аналитична в некоторой замкнутой односвязной области 
, за вычетом конечного числа особых точек 
, из которых ни одна не принадлежит граничному контуру 
, то справедлива следующая формула:
, где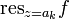 
— вычет в точке 
.
Из теоремы о В. вытекает теорема о полной сумме вычетов: если f(z) - однозначная аналитич. функция в расширенной комплексной плоскости, кроме конечного числа особых точек, то сумма всех В. функции f(z), включая В. в бесконечно удаленной точке, равна нулю.
38. Вычисления определенных интегралов по отрезку [0,2п] от рациональной функции относительно sint и cost и несобственных интегралов с бесконечными пределами рациональных функций.
Рассмотрим интеграл вида
,
где R (x) – рациональная функция, 
, причем многочлен Q (x) не обращается в нуль на вещественной оси и его степень по крайней мере на две единицы больше степени числителя. В этом случае интеграл сходится и его значение определяется по формуле
,
Вычисления определённых интегралов от тригонометрических функций
Пусть функция 
— рациональная функция переменных 
и 
. Для вычисления интегралов вида 
удобно использовать формулы Эйлера. Положив, что 
, и произведя соответствующие преобразования, получим:
.
Леммы Жордана. Несобственные интегралы по действительной оси от функций
( Лемма Жордана ). Если f(z) ÎC¥(Imz>0. z1,z2,...,zN¹¥) и f(z)=>0 при |z|®¥(равномерно по arg z, Im z >0), то при ReZ>0
CR - полуокружность | z |= R Im z >0.
Пусть R (x) - рациональная функция, не имеющая особых точек на действительной оси, для которой точка z, равная бесконечности, - нуль порядка не ниже первого.
Тогда справедливы формулы:
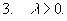
Преобразование Лапласа. Условия на функцию - оригинал.
Пусть имеем функцию действительного переменного f(t), которая удовлетворяет следующим условиям:
1) f(t) однозначна и непрерывна вместе со своими производными n-го порядка для всех t, кроме тех, где она и ее производные имеют разрывы 1-го рода. При этом в каждом конечном интервале изменения t имеется конечное число точек разрыва;
2) f(t)=0 для всех t<0;
3) f(t) возрастает медленнее некоторой экспоненциальной функции 
, где М и а - некоторые положительные величины, т.е. всегда можно указать такие М и а, чтобы при любом t>0 соблюдалось неравенство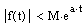 
.
В операционном исчислении функции f(t) ставится в соответствие новая функция F(p), определяемая равенством
Где p - положительное действительное число или комплексное число с положительной действительной частью.
Функция f(t) при этом называется оригиналом, а F(p)- изображением функции f(t) по Лапласу.
