Однородные ДУ. Уравнения сводящиеся к однородным

Основные понятия теории дифференциальных уравнений

Дифференциальное уравнение – уравнение, связывающее независимую переменную, искомую функцию и ее производные. Решение – функция, которая при подстановке в уравнение обращает его в тождество.

Если искомая функция зависит от одной переменной – ДУ называют обыкновенным, в противном случае – ДУ в частных производных. Наивысший порядок

Дифференциальные уравнения 1-го порядка. Задача Коши, теорема о существовании и единственности ее решения. Общее, частное решение (интеграл), особое решение.

F(x;y;y ^’)=0 – ДУ 1-го порядка(1)

y ^’ =f(x;y) ДУ, разрешенное относительно производной(2)

P(x;y)dx+Q(x;y)dy=0 – дифференциальная форма(3)

Задача отыскания решения ДУ 1-го порядка, удовлетворяющего заданному начальному условию (y(x₀)=y₀), называется задачей Коши.

Т. Если в уравнении (2) функция f(x;y) и ее частная производная f_y ^’ (x;y) непрерывны в некоторой области D, содержащей точку (x₀;y₀), то существует единственное решение y=φ(x) этого уравнения, удовлетворяющее начальному условию.

Общее решение - функция y=φ(x;с) содержащая произвольную постоянную.

Частное решение – функция y=φ(x;с₀) полученная из общего решения при значении постоянной с=с₀.

Если общее решение найдено в неявном виде Ф(x;y;c)=0, то оно называется общим интегралом ДУ. А Ф(x;y;c₀)=0 частный интеграл уравнения.

Функция φ(x;c) называется особым решением дифференциального уравнения F(x,y,y') = 0, если единственность решения нарушается в каждой точке этой функции в области определения дифференциального уравнения.

Геометрическая интерпретация ДУ 1-го порядка. Метод изоклин

Уравнение y ^’ =f(x;y) устанавливает связь между координатами точки и угловым коэффициентом y ^’ касательной к интегральной кривой. ДУ дает поле направлений на плоскости Оxy. Кривая, во всех точках которой направление поля одинаково называется изоклиной. Изоклинами можно пользоваться для приближенного построения интегральных кривых. Уравнение изоклины f(x;y)=с.

Уравнения с разделяющимися переменными

Уравнение с разделенными переменными: P(x)dx+Q(y)dy=0

Общий интеграл ДУ: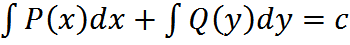

Уравнение с разделяющимися переменными: P₁(x)Q₁(y)dx+P₂(x)Q₂(y)dy=0 Можно привести к ДУ с разделенными переменными поделив на Q₁(y) и P₂(x)

Однородные ДУ. Уравнения сводящиеся к однородным

Функция f(x;y) называется однородной функцией n-го порядка, если при умножении каждого ее аргумента на произвольный множитель λ вся функция умножится на λⁿ, т.е. f(λ x; λ y)= λⁿ f(x;y). ДУ y ^’ =f(x;y) называется однородным если функция f(x;y) есть однородная ф-я нулевого порядка

P(x;y)dx+Q(x;y)dy=0 дифференциальная форма однородного ДУ

Уравнение вида 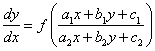можно свести к однородному типу. Нужно составить систему вида:
Пусть решение этой системы: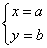

Тогда, для приведения уравнения к однородному типу необходимо сделать подстановку вида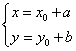
Если система не имеет решения следует сделать замену 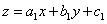.