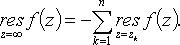Ряд Тейлора. Пусть функция w = f (z) аналитична в области D, 
. Обозначим L окружность с центром в z 0, принадлежащую области D вместе с ограниченным ею кругом. Тогда для любой точки z, лежащей внутри L, 
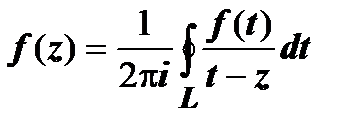. Представим множитель 
в виде суммы сходящейся геометрической прогрессии: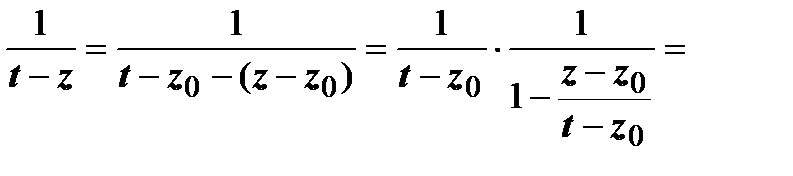 
(так как
| z – z 0| < | t – z 0|, то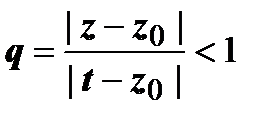 
) 
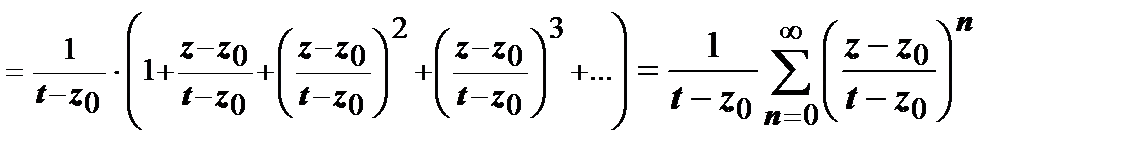, и ряд сходится абсолютно, поэтому его можно почленно интегрировать: 
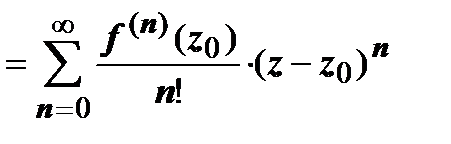, так как 
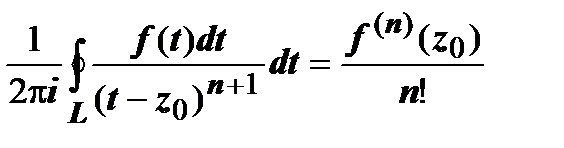. Итак,
.
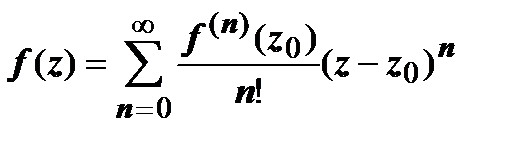Ряд в правой части этого равенства - ряд Тейлора функции f (z). Этот ряд абсолютно сходится внутри контура L, а в качестве L можно взять любую окружность, которая не выходит за пределы области D. Доказана
Ряд Лорана. Пусть функция f (z) аналитична в кольце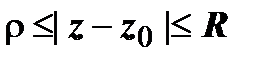 
. Тогда для любой точки этого кольца 
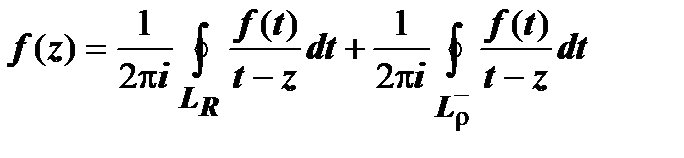; при этом окружности проходятся так, что область остаётся слева
Нули аналитических функций. Правила определения порядка нулей.
Определение. Точка а называется нулём порядка k аналитической функции f (z), если f (a) = f ′(a) = f ″(a) =... = f (k −1)(a) = 0, но f (k)(a) ≠ 0.
Пример. Пусть 
. Точка a = 0 - нуль этой функции, так как f (0) = 0. Найдём порядок нуля:
f ″(z) = − sin z + z, f ″(0)= 0,
f (3)(z) = − cos z + 1, f (3)(0) = 0,
f (4)(z) = sin z, f (4)(0) = 0,
f (5)(z) = cos z, f (5)(0) = 1 ≠ 0,. Первая отличная от нуля производная функции в точке a = 0 - пятая, поэтому эта точка - нуль пятого порядка функции .
Классификация особых точек ФКП. Изолированные особые точки.
Точка а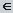 
Сz называется изолированной особой точкой однозначного характера функции f (z), если f (z) аналитическая и однозначная (регулярная) в кольце { z:0<| z – a |< }, а в самой точке а не определена.
Бесконечно удаленная точка называется изолированной особой точкой однозначного характера функции f (z), если f (z) регулярна в некоторой окрестности { R <| z |< 
} точки z= и функция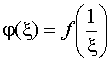 
имеет в точке = 0 изолированную особую точку однозначного характера.
В зависимости от поведения функции f (z) вблизи точки а различают следующие три типа особых точек.
Изолированная особая точка а функции f (z) называется
а) устранимой особой точкой, если существует конечный предел
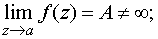
б) полюсом, если
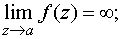
в) существенно особой точкой, если
не существует.
Вычеты, их вычисление в особых точках. Вычет в бесконечно удаленной точке.
Вычет относительно бесконечно удаленной точки
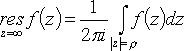
(f(z) - аналитическая в области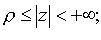 
обход контура - по часовой стрелке).
c-1 - коэффициент при z-1 в разложении f(z) в ряд Лорана в окрестности точки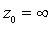 
.
Вычисление вычета в бесконечно удаленной точке
1. 
- правильная точка:
- нуль: 
В частности, если 
при 
то
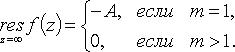
2. - полюс порядка не выше m:
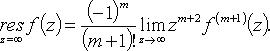
3. Если f(z) представима в ви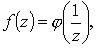де 
где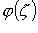 
- аналитическая в точке 
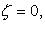то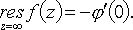 
Если f(z) имеет конечное число особых точек zk, k = 1, 2,..., n, в конечной части плоскости, то 
