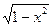|
|
101.
в) у = 2arctg х ∙arcsin 2х, г) у = lncos 6х д) 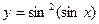
| |||
| |||
102.
в) у = еsin х ∙ arctg 4х г) у = sinln 7х д) 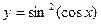
| |||
| |||
103.
|
|
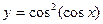
 104.
104.
в) у = еarcsin х ∙ cos 4х, г) у = arctg ln 5х д) 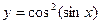
| |||
| |||
105.
у = 56х ∙ arcsin 5х, г) у = lnsin 7х д) 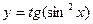
|
| ||||
106  .
.
|
|
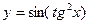
107.
в) у = 4tg х ∙ arctg 3х, г) у = lncos 4х д) 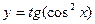
|
| ||||
 108.
108.
в) у = ех² · arcsin 2х, г) у = arctg ln 5х д) 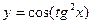
| |||
| |||
 109.
109.
в) у = 5аrctgх · sin 4х, г) у = ln arcsin 3х д) 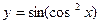
|
| ||||
110.
в) у = еarcsin х · ctg 3х г) у = arctg ln 8х д) 
111-120. Найти производные второго порядка от функций:
111. у = cos3х · еsinх у = lnarctg 2x
112. у = 23х · tg2х у = cosln 5х
113. у = еtgх · ln2х у = cos 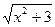
114. у = 28х · tg3х у = arcsin ln4х
115. у = еtgх · sin4х у = sin ln5х
116. у = 3ctgх · arcsin (х2) у = lnsin 6х
117. у = есtgх · cos6х у = sin ln2х
118. у = 4cosх · arctg2х у = lncos 5х
119. у = ех² · tg7х у = arcsin ln2х
120. у = 2sinх · arcsin2х у = lncos 7х
121-130. Найти производные указанного порядка от функций:
121. у(15) для у = cos5х 122. у(5) для у = (ex + e–x)/2
123. у(9) для у = sin7х 124. у(7) для у = sin(1–2х)+ 32х
125. у(83) для у = e2x 126. у(5) для у = cos7x + lnx
127. у(71) для у = 5–3x 128. у(14) для у = log5 x
121. у(5) для у = (ex – e–x)/2 122. у(11) для у = х1/2
|
|

 131. а) б)
131. а) б)

|
|
|
132. а) б)
 |  | ||||
|
в)
 | |||||
|
|
133. а) б)
 | |||||||
 | |||||||
 | |||||||
|
в)
 | |||||
|
|
134. а) б)
 |  | ||||
|
 в)
в)
|
|
 |  | ||||
|
 в)
в)
|
|
136. а) б)
 | |||||
 | |||||
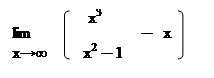 |
 в)
в)
|
|
 |  | ||||
 |

 в)
в)
|
|
138. а) б)
 |  | ||||
|
 в)
в)
|
|
139. а) б)
 |  | ||||
|
в)
 |
|
|
 |  |
|
 в)
в)
Применения дифференциального исчисления
141-150. Исследовать функции и построить их графики.
Исследования функций и построение графиков рекомендуется проводить по следующей схеме:
1. Найти область определения функции.
2. Исследовать на четность, нечетность, периодичность.
3. Найти точки пересечения графика функции с осями координат.
4. Исследовать функцию на непрерывность, найти точки разрыва функции и ее односторонние пределы в точках разрыва.
5. Найти точки экстремума функции и интервалы ее монотонности.
6. Найти точки перегиба, интервалы выпуклости и вогнутости графика функции.
7. Найти асимптоты графика функции.
8. Построить эскиз графика, используя результаты предыдущих исследований.
141. а) у = 2х3 + 3х2 – 36х – 21
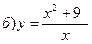 в) у = 2sin2 2х +1, 0 £ x £ p/2
в) у = 2sin2 2х +1, 0 £ x £ p/2
142. а) у = 2х3 + 15х2 + 36 + 32
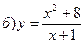 в) у = –cos2 2х +2, p/4 £ x £ p/4
в) у = –cos2 2х +2, p/4 £ x £ p/4
143. а) у = 2х3 – 15х2 + 24х + 4
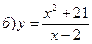 в) у = – ln2 |х|
в) у = – ln2 |х|
144. а) у = 2х3 – 9х2 – 24х + 61
 в) у = e sinx – 2, 0 £ x £ p
в) у = e sinx – 2, 0 £ x £ p
145. 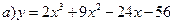
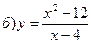 в) у = 2cosx, – p £ x £ p
в) у = 2cosx, – p £ x £ p
146. 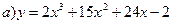
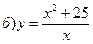 в) у = – arcsin|x| + p/2, –1£ x £ 1
в) у = – arcsin|x| + p/2, –1£ x £ 1
147. 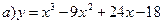
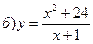 в) у = – arccos|x| – p
в) у = – arccos|x| – p
148. 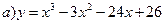
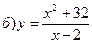 в) у = – 2arctgx2
в) у = – 2arctgx2
149. 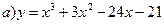
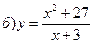 в) у = – 2xsinх, p/2 £ x £ p/2
в) у = – 2xsinх, p/2 £ x £ p/2
150. 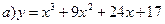
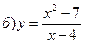 в) у = 3–sinx, – p/2 £ x £ p
в) у = 3–sinx, – p/2 £ x £ p
151-160. Найти наибольшее и наименьшее значения функции у = f(х) на отрезке [α; β] и написать уравнения касательной и нормали к кривой у = f(х) в точке х0:
151. 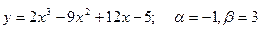 , х0=1
, х0=1
152.  , х0=–1
, х0=–1
153. 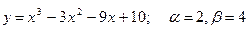 , х0=2
, х0=2
154. 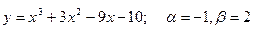 , х0=–2
, х0=–2
155. 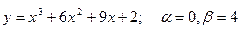 , х0=1
, х0=1
156. 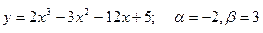 , х0=–1
, х0=–1
157. 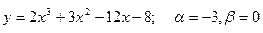 , х0=3
, х0=3
158. 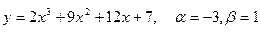 , х0=–3
, х0=–3
159. 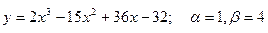 , х0=1
, х0=1
160. 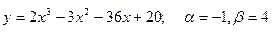 , х0=2
, х0=2
Неопределенный интеграл
161-170. Вычислить неопределенные интегралы. В пунктах а) и б) результаты проверить дифференцированием.
161. 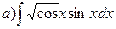
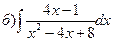
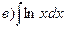
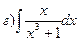
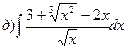
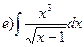
162. 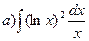
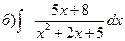
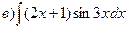
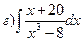
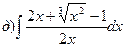
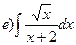
163. 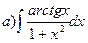
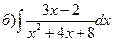
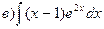
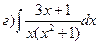
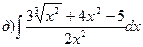
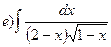
164. 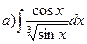
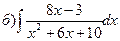
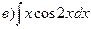
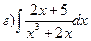
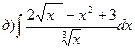
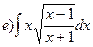
165. 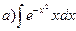
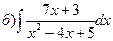
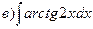
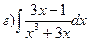
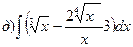
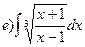
166. 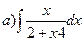
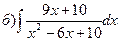
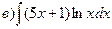
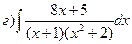
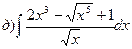
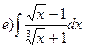
167. 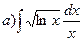
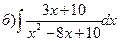
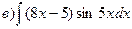
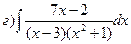
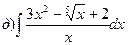
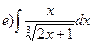
168. 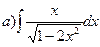
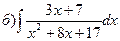
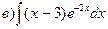
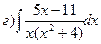
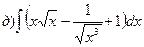
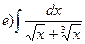
169. 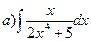
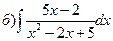
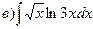
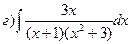
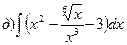
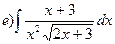
170. 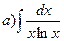
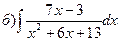
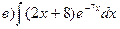
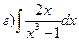
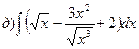
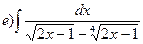
Определенный интеграл
171-180. Вычислить определенные интегралы:
171. 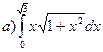
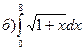 172.
172. 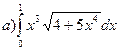
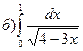
173. 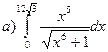
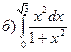 174.
174. 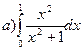
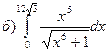
175. 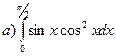
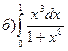 176.
176. 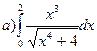
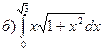
177. 
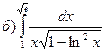 178.
178. 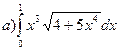
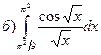
179. 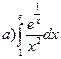
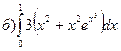 180.
180. 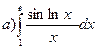
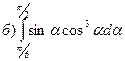
181-190. Вычислить площадь фигуры, ограниченной заданными кривыми:
181. a) 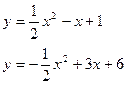 б)
б) 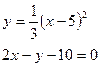 в)
в) 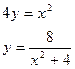
182. a) 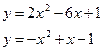 б)
б) 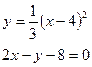 в)
в) 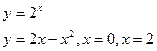
183. а) 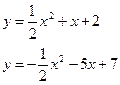 б)
б) 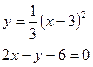 в)
в) 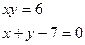
184. а) 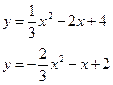 б)
б) 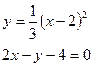 в)
в) 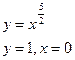
185. а) 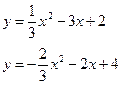 б)
б) 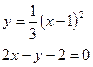 в)
в) 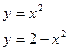
186. а) 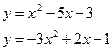 б)
б) 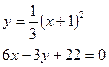 в)
в) 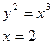
187. а) 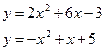 б)
б) 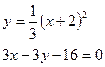 в)
в) 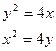
188. а) 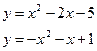 б)
б) 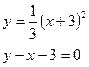 в)
в) 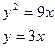
189. а) 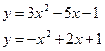 б)
б) 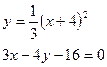 в)
в) 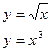
190. а) 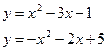 б)
б) 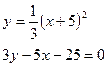 в)
в) 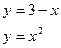
191-200. Вычислить объем тела, образованного вращением вокруг а) оси ОХ, б) оси OY фигуры, ограниченной линиями.
191. 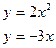 192.
192. 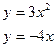 193.
193. 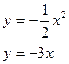 194.
194. 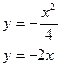
195. 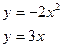 196.
196. 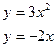 197.
197. 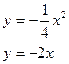 198.
198. 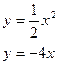
199. 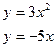 200.
200. 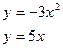
201-210. Вычислить приближенно данные интегралы, пользуясь формулой Симпсона и формулой трапеций. Если интеграл вычисляется точно, сравнить его приближенное значение с точным. (Число n частичных интервалов задается в скобках).
201. а) 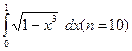 202. а)
202. а) 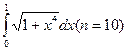
б) 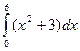 (n=6) б)
(n=6) б) 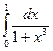 (n=6)
(n=6)
203. а) 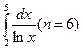 204. а)
204. а) 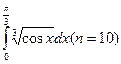
б) 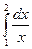 (n=8) б)
(n=8) б) 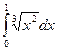 (n=8)
(n=8)
205. а) 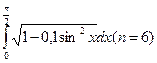 206. а)
206. а) 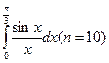
б) 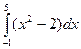 (n=8) б)
(n=8) б) 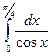 (n=6)
(n=6)
207. а) 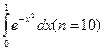 208. а)
208. а) 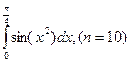
б) 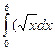 (n=10) б)
(n=10) б) 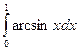 (n=6)
(n=6)
209. а) 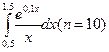 210. а)
210. а) 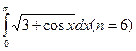
б) 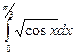 (n=6) б)
(n=6) б) 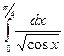 (n=6)
(n=6)





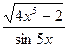
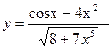
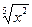 – 7)3
– 7)3

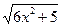
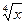 + 5)6,
+ 5)6,
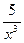 – 7)4,
– 7)4,
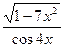
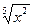 – 2)4,
– 2)4,
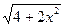
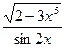
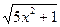
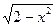 б) у =
cos 2х
б) у =
cos 2х
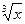 – 1)4,
– 1)4,
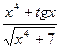
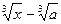 lim
х→а
lim
х→а 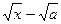
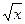 – 1
lim
х→о √ sin вх
– 1
lim
х→о √ sin вх