Элементы векторной алгебры и аналитической геометрии.
1-10. Найти векторное произведение  векторов
векторов  ,
,
 , угол между
, угол между  и
и  , угол между диагоналями параллелограмма, построенного на векторах
, угол между диагоналями параллелограмма, построенного на векторах  и
и  .
.
1. 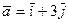 ,
,  2.
2.  ,
, 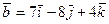
3.  ,
,  4.
4.  ,
, 
5. 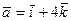 ,
,  6.
6.  ,
, 
7.  ,
, 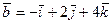 8.
8.  ,
, 
9.  ,
,  10.
10. 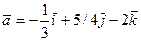 ,
, 
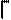 11-20. Даны координаты вершин треугольника АВС. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) внутренний угол В в радианах с точностью до 0,01; 4) уравнение медианы АЕ; 5) уравнение и длину высоты СD; 6) уравнение прямой, проходящей через точку Е параллельно стороне АВ и определить координаты точки пересечения этой прямой с высотой СD; 7) уравнение окружности, для которой медиана АЕ является диаметром; 8.) доказать, что
11-20. Даны координаты вершин треугольника АВС. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) внутренний угол В в радианах с точностью до 0,01; 4) уравнение медианы АЕ; 5) уравнение и длину высоты СD; 6) уравнение прямой, проходящей через точку Е параллельно стороне АВ и определить координаты точки пересечения этой прямой с высотой СD; 7) уравнение окружности, для которой медиана АЕ является диаметром; 8.) доказать, что  и
и  образуют базис в R2 и разложить
образуют базис в R2 и разложить  в этом базисе.
в этом базисе.
Сделать чертеж.
11. А (4; 0), В (7; 4), С (8; 2)
12. А (2; 2), В (5; 6), С (6; 4)
13. А (0; 2), В (3; 6), С (4; 4)
14. А (4; 1), В (7; 5), С (8; 3)
15. А (3; 2), В (6; 6), С (7; 4)
16. А (-2; 1), В (1; 5), С (2; 3)
17. А (4; -3), В (7; 1), С (8; -1)
18. А (-2; 2), В (1; 6), С (2; 4)
19. А (5; 0), В (8; 4), С (9; 2)
20. А (2;3), В (5, 7), С (6; 5)
21-30. Привести к нормальному виду уравнение окружности.
21.  22.
22.  23.
23. 
24.  25.
25.  26.
26. 
27.  28.
28.  29.
29. 
30. 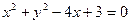
31-40. Установить, какие линии определяются нижеследующими уравнениями. Найти полуоси, фокусы, эксцентриситеты соответствующих кривых. Построить чертеж.
31.  32.
32.  33.
33. 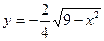 34.
34. 
35.  36.
36.  37.
37.  38.
38. 
39.  40.
40. 
Элементы линейной алгебры

 41-50. Решить систему уравнений по правилу Крамера.
41-50. Решить систему уравнений по правилу Крамера.

 41. 3х + 2у + z = 5 5х + 8у – z = –7 42. х + 2у + 4z = 31 х + 2у + z = 4
41. 3х + 2у + z = 5 5х + 8у – z = –7 42. х + 2у + 4z = 31 х + 2у + z = 4
а) 2х + 3у + z = 1 б) х + 2у + 3z = 1 а) 5х +у + 2z = 29 б) 3х – 5у + 3z = 1
2х + у + 3z = 11 2х – 3у + 2z = 9 3х – у + z = 10 2х + 7у – 7z = 8
 | |||||||
 | |||||||
 |  | ||||||
43. 4х – 3у +2z = 9 3х + 2у + z = 5 44. 3х – у = 5 х + 2у + 4z = 31
а) 2х + 5у – 3z = 4 б) 2х + 3у + z = 1 а) –2х + у + z = 0 б) 5х +у + 2z = 29
5х + 6у – 2z = 18 2х + у + 3z = 11 2х – у + 4z = 15 3х – у + z = 10
 | |||||
 |  | ||||
 45. 3х – у + z = 4 4х – 3у +2z = 9 46. 2х – у – 3z = 3 3х – у = 5
45. 3х – у + z = 4 4х – 3у +2z = 9 46. 2х – у – 3z = 3 3х – у = 5
а) 2х – 5у – 3z = –17 б) 2х + 5у – 3z = 4 а) 3х + 4у – 5z = 8 б) –2х + у + z = 0
х + у – z = 0 5х + 6у – 2z = 18 2у + 7z = 17 2х – у + 4z = 15
 |


 47. 3х + 4у + 2z = 8 х + у + 2z = – 1 48. 2х + у + 4z = 20 3х – у = 5
47. 3х + 4у + 2z = 8 х + у + 2z = – 1 48. 2х + у + 4z = 20 3х – у = 5
а) 2х – у – 3z = –1 б) 2х – у + 2z = – 4 а) 2х – у – 3z = 3 б) –2х + у + z =0
х + 5у + z = 0 4х + у + 4z = –2 3х + 4у – 5z = – 8 2х – у + 4z = 15
 | |||
 | |||

 49. х + 5у – z = 7 3х – у + z = 4 50. 11х + 3у – z = 2 х + у + z = 2
49. х + 5у – z = 7 3х – у + z = 4 50. 11х + 3у – z = 2 х + у + z = 2
а) 2х – у – z = 4 б) 2х – 5у – 3z = –17 а) 2х + 5у – 5z = 0 б) 2х – у – 6z = – 1
3х – 2у + 4z = 11 х + у – z = 0 х + у + z = 2 3х – 2у = 8
51-60. Найти:
а) обратную матрицу А-1 для матрицы А. Проверить равенство А · А-1 = А-1 · А = Е, где Е – единичная матрица,
б) матрицу D=AB-BA+A-1 +BT, здесь BT получается из В её транспонированием.
 |  |  |  |



 1 2 –3 2 3 – 2 1 2 –3 2 3 –2
1 2 –3 2 3 – 2 1 2 –3 2 3 –2
51. А = –1 –1 2, В= 0 0 3 52. А = 0 1 2, В= 1 2 3
2 4 –5 3 5 – 4 0 0 1 1 1 2
 | |||||||||||||||
 |  |  | |||||||||||||
 |  |  |  | ||||||||||||
3 –4 5 4 – 3 6 1 2 2 2 3 3
53. А = 2 –3 1, В= 3 – 2 2 54. А = 2 1 –2, В= 3 2 –1
3 –5 –1 4 – 4 0 2 –2 1 3 –1 2
 |  |  |  | ||||||||
 |  | ||||||||||
 0 1 3 1 2 4 1 3 5 2 4 6
0 1 3 1 2 4 1 3 5 2 4 6
55. А = 2 3 5, В= 3 4 6 56. А = 2 7 –8, В= 3 8 –7
3 5 7 4 6 8 –1 –3 4 0 –2 5
 |  |  |  |



 1 2 –3 2 3 –2 5 3 1 6 4 2
1 2 –3 2 3 –2 5 3 1 6 4 2
57. А = 3 2 –4, В= 4 3 –3 58. А = 1 –3 – 7, В= 2 –2 –1
2 –1 0 3 0 1 –5 2 1 – 4 3 2
 | |||||||||||||||
 |  | ||||||||||||||
 | |||||||||||||||
 |  |  |  | ||||||||||||
1 –2 –3 2 –1 –2 1 –2 2 2 –1 3
59. А = 1 –1 –2, В= 2 0 –1 60. А = 2 –5 7, В= 3 – 4 8
2 –3 –4 3 –2 –3 4 9 –10 5 10 –9
61-70. Решить системы уравнений двумя способам: 1) методом Гаусса, 2) средствами матричного исчисления.
 | |||
 | |||
61. 5х + 8у – z = – 7 62. х + 2у + z = 4
х + 2у + 3z = 1 3х – 5у + 3z = 1
2х – 3у + 2z = 9 2х + 7у – z = 8


63. 2х – у – z = 4 64. х + у + 2z = – 1
3х + 4у – 2z = 11 2х – у + 2z = – 4
3х – 2у + 4z = 11 4х + у + 4z = – 2
 | |||
 | |||
65. х + у + z = 2 66. 2х + у – z = 1
2х – у – 6z = – 1 х + у + z = 6
3х – 2у = 8 3х – у + z = 4

 67. х + 5у + z = -7 68. х – 2у + 3z = 6
67. х + 5у + z = -7 68. х – 2у + 3z = 6
2х – у – z = 0 2х + 3у – 4z = 16
х – 2у – z = 2 3х – 2у – 5z = 12
 |  |
69. 2х – у + 3z = 7 70. х – у = 4
х + 3у – 2z = 0 2х + 3у + z = 1
2у – z = 2 2х + у + 3z = 11
Введение в математический анализ
71-80. Найти пределы числовых последовательностей хn.
|
| 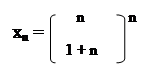 |


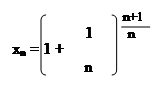
 71.
71.
 | |||||
| |||||
| |||||


 72.
72.
 | |||
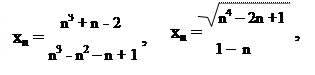 |


 73.
73.
|





|
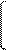
|
|  | ||||
 | |||||



 75.
75.
|  | ||||
| |||||



 76.
76.
 | |||
 |



 77.
77.
 | |||
 | |||


 78.
78.
 | |||||
 | |||||
 | |||||

 79.
79.
 | |||
 |
 80.
80.
81-90. Найти указанные пределы функций, не пользуясь правилом Лопиталя.
|
81. а) а = 2; б) а = –2; в) а = ∞
 | ||||||
 |  | |||||
|
82. а) а = 1; б) а = 2; в) а = ∞
 | |||||
 |  |

|
 | |||||
 |  | ||||
|
84. а) а = – 1; б) а = 1; с) а = ∞
 | |||||
 |
|

 | |||
|
85. а) а = 2; б) = – 2; в) а = ∞
 | |||
|


|
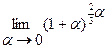
|
86. а) а= 1; б) а = 2; в) а = ∞
 |
|
|

|
 | |||
|
87. а) а = – 2; б) а = – 1; в) а = ∞
 | |||||
|  |


88. а) а = – 1; б) а = 1; в) а = ∞

|
|



|
 89. а) а = 2; б) а = – 2; в) а = ∞
89. а) а = 2; б) а = – 2; в) а = ∞
|
|



|
90. а) а = 1; б) а = 2; в) а = ∞
 | |||
|

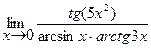 ,
, 
91-100. Функция у задается различными аналитическими выражениями для различных областей изменения аргумента х. Требуется: 1) найти точки разрыва функции у; 2) найти односторонние пределы и скачок функции в точке разрыва; 3) сделать чертеж.
 |  |
91. у = х2– 4, если х ≤ 2 92. у = 9– х2, если х ≤ 1
6–2х, если х > 2 2х+3, если х > 1
 | |||
 | |||
93. у = 4х+5, если х ≤ -1 94. у = х2+2х, если х ≤ 2
х2-4х, если х > -1 х+1, если х > 2
 |  |
95. у = 2х+3, если х ≤ -1 96. у = 4-х2, если х ≤ -2
3х-х2, если х > -1 3х + 2, если х > -2
 |  |
97. у = х2-2х, если х < 1 98. у = 4х+х2, если х < -2
1-4х, если х ≥ 1 2х+4, если х ≥ -2
 | |||
 | |||
99 у = х2+1, если х ≤ 2 100. у = х2-5, если х ≤ 1
х-3, если х > 2 1-3х, если х > 1




