Определитель, имеющий две равных строки (два равных столбца), равен нулю.
Если одну из строк определителя умножить на какое-либо число, то получится определитель, равный исходному, умноженному на это число.
Определитель транспонированной[3] матрицы равен определителю исходной матрицы.
Если в определителе вместо любой строки записать сумму этой строки и любой другой строки, умноженной на некоторое число, то полученный новый определитель будет равен исходному.
До сих пор было показано, как вычислять определитель второго и третьего порядков. Чтобы вычислить определитель более высоких порядков, пользуются формулой Лапласа разложения определителя по строке или столбцу:
det A = ai 1(–1) i +1 M i 1 + ai 2(–1) i +2 M i 2 +¼+ ain (–1) i + n M in =
= a 1 j (–1) 1+ j M 1 j + a 2 j (–1) 2 + j M 2 j +¼+ anj (–1) n + j M nj
Здесь i и j — любые числа от 1 до n. Последняя формула представляет собой разложение определителя по i -й строке или j -му столбцу. Mij называется минором и равняется определителю порядка n – 1, который получается из определителя det A, если вычеркнуть i -ю строку и j -й столбец. Произведение
(–1) i + j Mij обозначается Aij и называется алгебраическим дополнением элемента aij.
Пусть D – определитель четвертого порядка: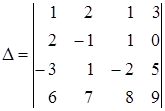 
. Представим его разложение по второй строке:
,
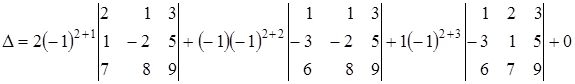и по второму столбцу:
.
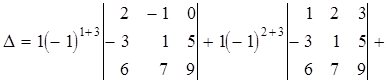
Аналогичным образом можно вычислить D, разлагая его по первой, третьей, четвертой строке или по первому, второму или четвертому столбцу.
Вычисление определителя четвертого порядка сводится в худшем случае (если среди элементов нет нулей) к вычислению четырех определителей третьего порядка.
Аналогичным образом вычисление определителя 5-го порядка сводится к вычислению 5-ти определителей 4-го порядка и т.д.
Для того, чтобы получить представление о том, что такое определительn-го порядка, не прибегая к определению на предыдущей странице, можно поступить так: выучить, как вычисляются определители 2-го и 3-го порядков и как по методу Лапласа сводить вычисление определителяn-го порядка к вычислению определителя n – 1-го порядка. Тогда становится понятным, как вычислять определитель 4-го порядка, затем 5-го порядка и т. д.
Из сказанного следует, что вычисление определителя 5-го порядка можно в общем случае свести к вычислению 20-ти(!) определителей 3-го порядка, что очень затрудняет задачу.
Вычисление определителя упрощается, если воспользоваться свойством 5. Пусть D – определитель четвертого порядка:
.
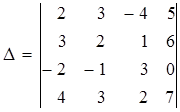Этот определитель разложим по третьей строке, так как там есть нуль и, что особенно важно, –1. Задача заключается в таком преобразовании определителя D, чтобы получить нули на месте a 31 и a 33. К первому столбцу прибавим второй столбец, умноженный на –2, а к третьему столбцу прибавим второй столбец, умноженный на –3. Второй столбец, с помощью которого проводились преобразования, остается без изменений.
Таким образом вычисление определителя 4-го порядка сведено к вычислению только одного определителя 3-го порядка:
.
Пусть теперь D — определитель 5-го порядка:
.
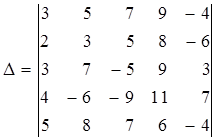Предположим, что мы решили разложить его по первому столбцу. Можно поступить следующим образом. Оставим первую строку без изменений. Вторую строку умножим на 3 и прибавим к ней первую, умноженную на –2. При этом обязательно за знак определителя выносится множитель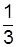 
(см. свойство 3). Вместо третьей строки пишем сумму третьей и умноженной на 
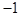первой. Четвертую строку умножаем на 3 и прибавляем первую, умноженную на –4, опять вынося множитель 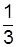за знак определителя. Пятую строку умножаем на 3, прибавляем к ней первую, умноженную на –5 и опять выносим 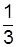за знак определителя. Теперь получим
.
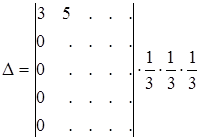Теперь вычисление определителя 5-го порядка сведено к вычислению только одного определителя 4-го порядка.
