В ПП свободные электроны и дырки нах в состоянии хаотического движения. При помещении ПП в электрическое поле с напряжённостью Е движение электронов и дырок упорядочивается: электроны приобретают преимущественно направление движения частиц против напряжённости эл. поля, и дырки - по направлению напряжённости. Направленное движение электронов и дырок вызывает протекание через ПП электрического тока, наз. дрейфовым. При измен. направления напряжённости электр. Поля изменяется и направление протекания дрейфового тока.
Движение электронов и дырок под действием эл. поля характер-ся подвижностью µ, определяемой как отношение средней скорости v подвижных носителей заряда к напряжённости эл. поля E: µ=v/Е (2.14).
Подвижность измеряется в м^2/(В*с) и имеет различные численные значения для электронов(µn) и дырок (µp).С увеличением температуры и концентрации примесей в ПП подвижность электронов и дырок уменьшается. Это вызвано увеличением числа их столкновений в единицу времени и уменьшением длины свободного пролёта.
Дрейфовый ток содержит две составляющие: электронную и дырочную. Так как электроны и дырки под дейсвием эл. поля движутся(дрейфуют) навстречу друг другу, то плотность дрейфового тока через ПП равна
jдр= jnдр+jpдр=qnv+qpv, где q-заряд электрона, n и p - концентрации соответственно электронов и дырок. С учётом (2.14): jдр=qnµnE+qpµpE=q(nµn+pµp)E (2.15)
Сравнение этих уравнений с законом Ома j= 
E( -удельная электропроводность) показывает, что удельная электропроводность ПП равна = n- p= q(nµn+pµp) (2.16)
Из выражения (2.16) следует, что для собственных(чистых) ПП I=qni(µn+µp)=qpi(µn+µp); для ПП n-типа 
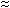
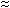
n=qnn0µn, а для ПП p-типа p=qpp0µp.
Кроме эл.поля причиной направленного движения электронов и дырок может быть их диффузионное движение, вызванное неравномерностью распределения их концентраций. Под действием сил диффузии электроны и дырки из области высокой концентрации перемещаются в область с меньшей концентрацией. Плотность диффузионного тока,как и дрейфующего, содержит 2 составляющие - электронную и дырочную, определяемые соответственно уравнениями: jn диф=qДndn(x)/dx, jp диф= -qДpdp(x)/dx, (2.17) где dn(x)/dx и dp(x)/dx - градиенты концентраций электронов и дырок в направлении x; Дn и Дp - коэффициенты диффузии электронов и дырок.
Градиент концентрации характеризует степень неравномерности распределения носителей заряда в ПП вдоль какого-то направления. Например, при равномерном распределении электронов в ПП в направлении x (рис. 1, прям.1) dn(x)/dx=0.Для распределений, показанных линиями 2 и 3 dn(x)/dx соответственно отрицательный или положительный.
Коэффициенты диффузий связаны с подвижностями соотношениями Эйнштейна:
Дn=µnkT/q, Дp=µpkT/q (2.18)
Знак "-" в (2.17) для jp диф поставлен потому, что в направлении протекания диффузионного тока градиент концентрации дырок dp(x)/d(x)<0.
Если в ПП существует градиент конц. подвижных носителей заряда и на него воздействует эл. поле с напряжённостью Е, то эл. ток в таком ПП содержит диффузионные и дрейфующие составляющие. При этом jn=qnµnE+qДndn(x)/dx (2.19) jp=qpµpE-qДpdp(x)/dx (2.20).
Диффузионное движение подвижных носителей заряда может наблюдаться и при равномерном первоначальном распределении концентрации носителей заряда, но при наличии в ПП разности (градиента) температур. В таком случае возникает диффузия подвижных носителей заряда из нагретых участков в более холодные.
Рис. 1 
