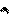 |
S – точка, где вода теряет свою сплошность (образуются капли). В ней минимальная насыщенность водой. Проницаемость от 0 до S равна 0.
 |
Начиная с S водяная фаза преодолевает порог перколяции, образуя фазу.
S* - точка, где нефть/газ перестаёт двигаться. В ней максимальная водонасыщенность. Нефть в объёме пор находится в связанном состоянии.
Sос=(1-S*) – характеризует долю нефти/газа, которые неподвижны – остаточная нефтенасыщенность.
В обоих случаях f<1.
0 – точка равенства проницаемостей по нефти и по воде.
Т.о. фазовая проницаемость характеризует фильтрационную способность пласта в присутствии другой фазы.
Рассмотрим трубу (D) с разным уровнем заполнения (Н)Þ
Qж1
ж2 
Qж2
Н ж1
Н/D
При изменении величины, изменяется сила сопротивления.
Этот эффект называется эффектом проскальзывания.
Если мы имеем аномальные жидкости, например насыщенные ПАВ.
Происходит повышение проницаемости (>1)
Факторы, влияющие на фазовую проницаемость:
1. геометрия структуры пор
2. градиент давления
3. характер смачивания пористой среды данной фазы
Чем сложнее конфигурация пор, тем сильнее выражена сила сопротивления.
Фазовые проницаемости трещинной среды выглядят следующим образом:
 |
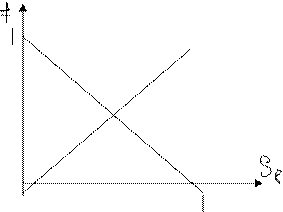Обнаружено, что наибольшее влияние имеет изменение структуры пор по воде, затем по нефти и ещё меньше по газу.
Фазовые проницаемости зависят от степени смачиваемости.
Для гидрофобного пласта «0» сдвигается в сторону уменьшения водонасыщенности.
 |
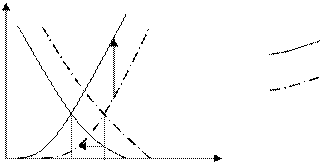– гидрофобный пласт
– гидрофильный пласт
Для гидрофобных пластов фазовая проницаемость по воде выше, чем для гидрофильных, следовательно: не следует заводнять гидрофобные пласты (они лучше проводят воду). В них присутствует эффект смазки. Жидкость встречает меньше сопротивления, т.к. поверхность не оказывает влияния на движение.
Целесообразнее рассматривать нормированные фазовые проницаемости.
kф(S)/kфf(S) kф/kо=kоf(S)
1 f(S) f(S*)
fн,в
S S*
Чтобы рассматривать насыщенность только в области, где существуют обе фазы, берут приведённую насыщенность.
s=(Sв– S)/(1– S –(1-S*))=(Sв- S)/(S*- S)
Нормированные фазовые проницаемости имеют более универсальный характер.
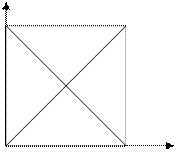fн,в
0 1 s
Рассмотрим условия совместного движения трёх фаз.
17. Условия совместного движения трёх фаз.
н 100%
 |
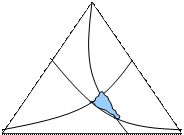в 100% г 100%
Необходимо определить такую характеристику, как удельная поверхность пласта.
Удельная поверхность – общая поверхность пор, приходящихся на единицу массы, или на единицу объёма (S).
[м2/кг] или [м-1]
Взаимосвязь между объёмной и массовой удельной поверхностью выражается следующим образом:
Sп=S×sтв×(1 – kп),
где Sтв – массовая удельная поверхность
Sп - объёмная удельная поверхность
sтв – плотность породы
Чем больше удельная поверхность, тем сильнее твёрдая фаза влияет на движение жидкости и газа.
Сужается диапазон фазовой проницаемости.
Способы определения.
1. разрушение породы (теряется структура);
2. шлиф;
3. используя породу как адсорбент, можно исследовать площадь адсорбции.
Sтв=Q/(m×s); s=3×10-7¼17×10-7 г×экв/м2,
где Q- количество адсорбируемого вещества;
s- количество вещества в монослое;
m- масса вещества.
18. Обобщённый закон Дарси.
Qн=(k0×/mн)×fн(S)×grаd(Рн)
Qв=(k0/mв)×fв(S)×grаd(Рв)
k0 – абсолютная проницаемость пласта.
Рн=Рв – Рк, где Рк – капиллярное давление.
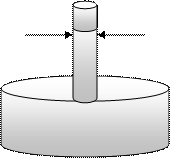Капиллярное давление свойственно системе, состоящей, по крайней мере, из трёх фаз.
Рк=2×s×соsq/rк,
rк
где соsq - косинус угла смачивания;
s - поверхность натяжения. в
Лекция №6.
19. Структура внутрипорового пространства и её влияние на фильтрационные и ёмкостные свойства.
Структура порового пространства – это характер распределения пор по размерам, форме и конфигурации, а также по взаимному расположению пор относительно друг друга.
Реальный элемент пор:
rк rк
rп rп
Для выявления закономерностей сначала выделяют маленькие поры – капилляры, а затем определяются радиусы пор.
Поры
Проточные Тупиковые
 |
От порометрической характеристики зависит извлечение нефти и газа.
Важным моментом является то, что у нас обычно результатом порометрической характеристики представляются функции распределения пор по размерам.
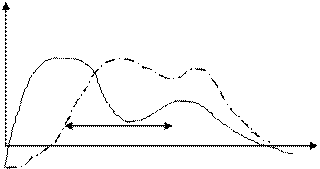
F(r)=dv/dR
1
 |
0 R
Rк Rп
Красная зависимость соответствует более хорошему пласту, т.к. капилляры обладают большим диаметром, а значит пропускная способность выше.
Функция F(r) характеризует объёмную долю распределения пор по размерам.
Кроме распределения пор по размерам, определяющим параметром является форма пор.
(См. ранее каверновые, трещинные типы пор).
Форма пор рассматривается с точки зрения их приближённости к правильным геометрическим фигурам:
Характеристика пор реального пласта:
Для изучения используются прямые методы, основанные на компьютерном анализе результатов изучения керна с помощью электронного растрового микроскопа.
Обрабатывая методом секущих, определяем конфигурацию, взаимосвязь пор и т.д.
Взаимосвязанность определяется координационным числом.
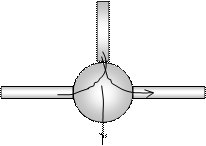Координационное число – количество капилляров, подходящих к одной крупной поре.
Когда для фильтрации
существует много путей,
часть объёма поры
может быть неохвачена
и эффективность вытеснения низкая.
Если rп>>rк, то такие поры будут вести себя как непроточные.
Крупные поры отвечают за запасы, капилляры – за извлечение, поэтому при определённом соотношении запасы будут трудноизвлекаемы.
Распределение пор по размерам можно определять разными способами: ртутное выдавливание, выдавливание центрифугой и другие.
Наиболее распространён способ центрифугирования, по опытным данным которого строится кривая зависимости капиллярного давления от водонасыщенности.
Рк
Sв
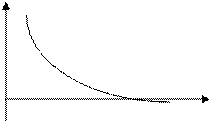
Функция капиллярного давления зависит от коллекторских свойств. Чем выше коэффициент k, тем более сдвинута кривая влево, тем ниже остаточная водонасыщенность.
Но всё же наша функция
неявным образом характеризует
распределение пор по размерам.
Sв
Стрелка указывает на возрастание k.
1 – ширина переходной зоны,
определяемая капиллярным давлением.
Высота переходной зоны может быть
более 30 м.
Одной из определяющих характеристик на практике является функция Леверетта.
Функция Леверетта – отношение капиллярног о давления к давлению, развивающемуся в порах среднего размера: _
I(S)=Рк(S)/Р
I(S)
S
Капиллярное давление имеет гистерезис, который определяется тем, какой процесс идёт:
ü увеличение насыщения водой (пропитка)
ü уменьшение насыщения водой (дренаж)
Соответствующие кривые для пропитки и дренажа совершенно разные:
Рк
Р0
S* S
Красная линия соответствует дренажу, синяя - пропитке.
Явление гистерезиса характерно и для кривых фазовой проницаемости. Кривые фазовой проницаемости определяются характером взаимодействия между фазой и пористой средой.
Модели проницаемости.
Модели показывают взаимосвязь проницаемости со структурой порового пространства.
1) Модель прямолинейных параллельных капилляров;
2) Модель извилистых параллельных капилляров; (согласно этой модели устроена формула Казени-Кармана).
3) Модель «капилляры с тупиковыми порами»
4) Серийные модели
 |
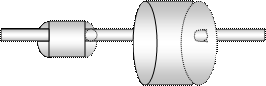5) Серийная модель из сферических полостей;
 |
6) Модель «периодически гофрированный капилляр»;
7) Модель «пора с диффузной копировкой»
 |
Если мы имеем модель параллельных капилляров, то расход через неё можно выразить следующим образом:
q=p×r4×Dр/(8×h×1),
где r – радиус капилляров; h - вязкость; 1 – длина капилляров.
k=n×p×r4/8, т.е. проницаемость – четвёртая функция от r.
В модели Казени-Кармана капилляры извилисты, следовательно:
k=p×r4×n/(8×x),
где x - некий коэффициент – коэффициент извилистости.
Если функцию распределения капилляров по размерам обозначить как j(r), доля капилляров которой лежит в области от r до r+dr и оказывает вклад на проницаемость на величину dk.
dk=p×n×r4×j(r)×dr/(8×x)
Интегрируя от r до r+dr, получим:
k=n×p/(8×x)0ò¥r4×j(r)×dr
Сейчас моделирование пласта идёт по линии усложнения структуры капилляров с использованием компьютера.
Введём новые обозначения:
F(r)dr – доля объёма порового пространства, приходящегося на интервал от r до r+dr.
F(r) – функция распределения объёма капилляров.
Тогда:
V=n×p×r2×S×dr×10×x=m×F(r)×dr×10×S,
где S – площадь, 10 – начальная длина, x - коэффициент извилистости.
x×n×r2×j(r)×dr=m×F(r)×dr
Т.о. связь проницаемости с функцией распределения объёма по размерам можно выразить следующим образом:
k=m/(8×x2)×0ò¥r2×F(r)×dr
Данная формула выражает связь проницаемости со структурой порового пространства, заданного как функции j(r) и F(r).
Пусть наши капилляры имеют неодинаковый радиус r, тогда графическая зависимость будет выглядеть следующим образом:
 |
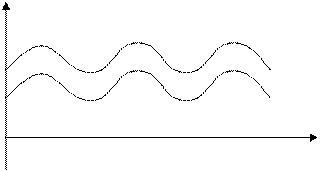r
r(х)
dr
х
В этом случае выполняется следующее соотношение:
p×r2×dr/(0òrp×r2×dr)=F¢(r)×dr,
где F¢(r) – функция распределения r по длине капилляра.
Обозначим 0òrp×r2×dr=А Þ А=m×10, тогда:
p×r2×x×dr=F¢(r)×dr×m×10/n,
где n – количество капилляров.
Используя закон Пуазейля, получим:
Dр=8×h×Q/(p×n)× 0ò¥dr/r4;
Dр=8×h×m×Q×10/(p2×n2)×0ò¥F¢(r)×dr/r6, Þ k=p×n2/(8×m×0ò¥F¢(r)×dr/r6)
Можно видеть, что функция капиллярного давления включает в себя данные структурного строения.
