≈сеп шарты: ћеханизм өзара т≥ст≥ немесе қайысты б≥рлест≥г≥ 1;2;3; сатылы дөңгелектерден, 4 т≥ст≥ рейкадан және ж≥пт≥ң шет≥не байлап дөңгелект≥ң б≥р≥не оралған 5-ш≥ жүктен тұрады (сурет 4.). ƒөңгелектерд≥ң сатыларының радиусы сәйкес≥нше: r1 = 20мм; R1=40 мм; r2 =60 мм; R2 = 80 мм;г2 = 120 мм; R3 =160 мм Ц ге тең. (r-дөңгелект≥ң к≥ш≥ радиусы, R-дөнгелект≥ң үлкен радиусы. —андық индекс дөңгелект≥ң есеп схемасындағы номер≥н б≥лд≥ред≥). ƒеңгелект≥ң бойында ј, ¬ және — нүктелер≥ орналасқан.
Ѕер≥лген қозғалыс заңы үш≥н көрсет≥лген звеноның немесе оның жылдамдығының өзгеру заңын уақыт момент≥н анықтау үш≥н, 4 кестеде көрсет≥лген шамаларды анықтау керек, және осы шамалардың векторларын есеп схемасында көрсет≥ндер. φ және ω сағат т≥л≥н≥ң бағытына қарсы болса, ал S4, S5 бағыттарытөмен бағытталса оң деп саналады.
≈септ≥ шығару үш≥н жалпы әд≥с.
1.—ызықтық масштабты сақтай отырып сатылы дөңгелектерд≥ есеп схемасында бейнелейм≥з.
2.Ѕер≥лген звеноның қозғалыс заңы бойынша оның жылдамдығын, уақыттың
функци€сы рет≥нде анықтаймыз (V4 = dS/dt немесе V5=dS5/dt), немесе ол арқылы
нүкте жылдамдығын және үдеу≥н өрнектеуге болады.
3.∆ылдамдықтан уақыт бойынша б≥р≥нш≥ туындысын алып үдеуд≥ уақыттың
функци€сы рет≥нде анықтаймыз.
4.Ѕер≥лген уакыттың мән≥н өрнекке қойып жылдамдықтың және үдеуд≥ң
сандық мәндер≥н табамыз.
5.∆ылдамдық және үдеу үш≥н масштаб алып табылған шамалардың
векторларын тұрғызамыз. Үдеуд≥ң векторын түрғызу үш≥н оны нормаль және
жанама үдеуге бөлу керек.

—урет 4. є4 есеб≥н≥ң схемасы.
есте 4
є4 есеб≥н≥ң варианттарының бер≥лген≥.

є4 есеб≥не мысал:
≈септ≥ң шарты: ћеханизм 1; 2; 3 сатылы дөңгелектерден, т≥ст≥ рейка 4 және 5 жүктен тұрады (сурет 4.1). ƒөңгелектерд≥ң радиустары сәйкес≥нше: r1 = 20мм; R1=40 мм; r2 =60 мм; R2=80 мм; г2 = 120 мм; R3 =160 мм. –ейканың қозғалыс заңы бер≥лген S4 = 9t-5t2, мұндағы S-см, t-секундпен. t1 =3,2 с уақыт момент≥ үш≥н анықтау керек: ω3, V4, ≈3, а4, а5, –ейканың қозғалысының оң бағыты - төмен.

—урет 4.1. є4 есепт≥ң мысалына есептеу схемасы.
|
|
|
Ўешу≥:
1.ƒөңгелект≥ң сыртқы құрсауындада жаткан нүктен≥ң жылдамдығын R радиуске сәйкес индекс≥мен, ал ≥шк≥ құрсауындағы - г аркылы белг≥леуге шарттасылған.–ейканың жылдамдығын қозғалыс заңынан уақыт бойынша б≥р≥нш≥ туынды рет≥нде анықтаймыз:
V4 = dS4/dt=9-10t (см/с) (1)
2.–ейкамен 2-ш≥ дөңгелект≥ң сыртқы құрсауы ≥л≥н≥сте болғандықтан, V 2= V4=9-10t (см/с), олай болса 2-ш≥ дөңгелект≥ң бұрыштық жылдамдығы:
w2= V2/ R2=1/R2*(9-10t) (c-1) (2)
Ѕұрыштық жылдамдық мән≥ дөңгелект≥ң барлық нүктелер≥ үш≥н б≥рдей болғандықтан, 2-ш≥ дөңгелект≥ң ≥шк≥ құрсауының сызықтық жылдамдығы:
U2= w2* r2= r2/R2*(9-10t) (см/с) (3)
≈к≥нш≥ дөңгелект≥ң ≥шк≥ құрсауымен 3-ш≥дөнгелект≥ң сыртқы құрсауы ≥л≥н≥сте болғандықтан, олардың айналу жылдамдықтары тең, демек
V3 = U2 = r2/R2*(9-10t) (см/с) (4)
олай болса 3-ш≥ дөнгелект≥ң бұрыштық жылдамдығы:
w3= V3/ R3= r2/R2 R3*(9-10t) (c-1) (5)
осы арқылы 3-ш≥ дөңгелект≥ң ≥шк≥ құрсауының айналу жылдамдығын анықтаймыз.
Ѕ≥р≥нш≥ дөңгелект≥ң сыртқы құрсауының айналу жылдамдығы да олармен ≥л≥н≥сте болғандықтан осы мәнге сәйкес болады:
V1=U3= r2 r3/ R2 R3*(9-10t) (см/с) (6)
Ѕ≥р≥нш≥ дөңгелект≥ң бұрыштық жылдамдығы келес≥ түрде анықталады:
w1= V1/ R1= r2 r3 /R2 R3R1*(9-10t) (c-1) (7)
ќсы жылдамдық бойынша 1-ш≥ дөңгелект≥ң ≥шк≥ құрсауының айналу жылдамдығын және 5 жүкт≥ң жылдамдығын анықтаймыз.
Ѕ≥р≥нш≥ дөңгелект≥ң ≥шк≥ құрсауының айналу жылдамдығын және 5-ш≥ жүкт≥ң жылдамдықтары тең болғандықтан осы жылдамдық бойынша анықтаймыз:
V5=U1=w1 r1 = r2 r3 r1 / R2 R3 R1*(9-10t) (см/с) (8)
w3 - тен уақыт бойынша б≥р≥нш≥ туынды алып анықтаймыз:
e3= -10 r2/R2 R3 (c-2) (9)
“ап осылай ј нүктес≥н≥ң жанама үдеу≥н және 5-ш≥ звеноның үдеу≥н табамыз:
aјt= dV3/dt=-10 r2/R2 (см/c2) (10)
a5= dV5/dt=-10 r2 r3 r1 / R2 R3 R1 (см/c2) (11)
ј нүктес≥н≥ң нормаль үдеу≥ келес≥ өрнектен анықталады:
aјn= V32/R3 = r22/R22 R3 *(9-10t) 2 (см/c2) (12)
ал осы нүктен≥ң толық үдеу≥:
 (13)
(13)
(1), (5), (9), (10),(11), (12), (≤«) теңдеулерге бер≥лген шамалардың сандық мән≥н б≥р өлшем б≥рл≥кте қойып, сәйкес≥нше табатынымыз:
V4 = 9-10*3,2=-23 (см/с)
w3= 6/ 8*16= (9-10*3.2)=-1,08 (c-1)
e3= -10 *6/ 8*16=-0,469 (c-2)
a5= -10 *6*12*2/ 8*16*4=-2,81 (см/c2)
aјt= -10*6 /8=-7,5 (см/c2)
aјn= 62/82 *16*(9-10*3,2) 2 =18,6 (см/c2)
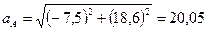 (см/c2)
(см/c2)
∆ылдамдықтар және үдеулер векторларын тұрғызу үш≥н алатынымыз;
|
|
|
- жылдамдықтар масштабын μv =0,13
- үдеулер масштабын μа =0,13
ќлай болса жылдамдықтар және үдеулер векторлары:
aјt= 1 см
aјn= 2,5см
aј= 2,7см
a5= - 0,37 см
V4 = -3 см
≈сеп є5






