Мета роботи: навчитись розв’язувати лінійні диференціальні рівняння з відокремлюваними змінними; знаходити їх загальні та часткові розв’язки.
Наочне забезпечення та обладнання:
1. Інструкційні картки
2. Приклади задач
3. Роздаткові матеріали: варіанти завдань
4. Обчислювальні засоби: калькулятор.
Теоретичні відомості про лінійні диференціальні рівняння з відокремлюваними змінними. Задача Коші
Означення. Диференціальне рівняння першого порядку називається рівнянням з відокремлюваними змінними, якщо воно має вигляд:
X(x)Y(y)dx+X1(x)Y1(y)dy=0, (1) де X(x), X1(x) – функції тільки відносно x, Y(y),Y1(y) – функції тільки відносно y.
Для розв’язування рівняння (1) поділимо обидві частини рівняння на добуток Y(y)X1(x), вважаючи, що вони не дорівнюють нулю. Тоді після очевидних скорочень матимемо:
dx + 
dy=0 (2)
В рівнянні (2) біля dx стоїть функція, що залежить лише від x, а при dy стоїть функція тільки від y. В цьому випадку говорять, що змінні відокремлені. Інтегруючи обидві частини рівняння (2), матимемо:
dx+ 
dy=C (3)
Під інтегралами розуміємо первісні функцій. Співвідношення (3) і представляє собою загальний інтеграл рівняння (1). В загальному випадку, коли ми ділимо рівняння (1) на добуток X1(x)Y(y), ми ризикуємо втратити ті розв’язки рівняння, які перетворюють даний добуток в нуль.
За допомогою безпосередньої підстановки легко переконатися, що функція
x = a, (4)
де a- корінь рівняння X1(x)=0, тобто X1(a)=0 є розв’язком рівняння (1).
Також y=b, де b - корінь рівняння Y(y)=0, (5) є розв’язком рівняння (1).
Геометрично розв’язки (4),(5), якщо вони існують, представляють прямі лінії, відповідно паралельні осі OY і осі OX.
Диференціальні рівняння описують багато процесів реального життя. Тому їх часто застосовують для розв’язання практичних, прикладних задач, зокрема задач з професійної діяльності спеціаліста сільського господарства.
Задача 1. Знайти загальний розв’язок рівняння 
= 
Задача 2. Знайти загальний розв’язок диференціального рівняння 
Задача 3. Знайти загальний розв’язок диференціального рівняння xy+y' 
=0 і його частковий розв’язок, що задовольняє початкову умову y(1)=1.
Питання для самоконтролю знань, умінь.
1. Яке рівняння називається диференціальним?
2. Яка функція називається розв’язком диференціального рівняння?
3. Що таке порядок диференціального рівняння?
4. Назвати відомі типи диференціальних рівнянь, їх основні характеристики.
5. Як розв’язувати диференціальні рівняння з відокремлюваними змінними?
6. В чому полягає задача Коші?
Виконаємо самостійно
В - 1 В - 2
1.Знайти загальний розв’язок диференціального рівняння:
. Знайти загальний та частковий розв’язки диференціального рівняння:
y(0)=3 y(0)= 
В - 1 В - 2
1.Знайти загальний розв’язок диференціального рівняння:
; 
;
. Знайти загальний та частковий розв’язки диференціального рівняння:
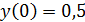
ПРАКТИЧНА РОБОТА № 17
