Все наблюдаемые процессы, характеризующие физические явления, делятся на детерминированные и случайные. Для случайного процессе исход любого данного наблюдения предстевляет собой лишь один из многих возможных результатов.
Рассмотрим результаты испытаний по росту усталостных трещин в плоских образцах из материала Д16АТВ. Испытания проводились на растяжение при Ϭа = 40 МПа, Ϭс =120 МПа. Ширина образцов 60 мм, толщина 2 мм, начальная длина трещины 0,05 мм. До разрушения било испытано 20 одинаковых образцов. На рис. 31 изображены выборочные функции (реализации) пк (t*) (К = I, 2,..., 20), соответствующие разным образцам с относительной длиной трещи t*, количеством циклов нагружения п.
Из рис. 31 видно, что процесс распространения усталостной трещины является случайным процессом, так как результат каждого испытания невоспроизводим. Более того, этот процесс является нестационарным случайным процессом, так как математическое ожидание и корреляционная функция меняются с изменением относительной длины трещины.
Теория нестационарных случайных процессов развита слабее теории стационарных и особенно эргодических процессов. До сих пор нет единой методики для анализа любых нестационарных процессов. Поэтому для таких процессов приходится разрабатывать специальные методы анализа, применимые только к некоторым вполне определенным типам нестационарных процессов.
Рис. 31
Отсюда следует, что сначала необходимо выяснить тип рассматриваемого нестационарного случайного процесса. Рассмотрим подробнее процесс развития усталостной трещины. Анализ реализаций (рис. 31) показывает, что рассматриваете нестационарный случайный процесс может быть описан соотношением
(24)
где n - количество циклов, соответствующее t *; n0 - количество циклов, соответствующее начальной относительной длине трещины t̽̽ 0; А - случайная велшиьа; ψ(t*)~ некоторая детерминированная функция.
Для дальнейшего анализа удобно ввести обозначения
| Тогда уравнение (24) пиймет вид |
(25)
где Х= X (t) - случайная функция; ψ(t) - детерминированная функция.
В соответствии с классификацией нестационарных случайных процессов определяемый соотношением (25) процесс относится к элементарному нестационарному случайному процессу. При этом случайная величина А называется координатой случайного процесса X, а детерминированная функция (ψ) - координатной функцией.
Элементарный нестационарный случайный процесс (25), характеризуемый фактически одной случайной величиной А, может быть отнесен к классу сингулярных (вырожденных) процессов, так как, чтобы знать всю реализацию этого процесса, достаточно произвести по крайней мере одно измерение при известной функции (ψ).
Используя полученные результата, рассмотрим прогнозирование процесса роста усталостных трещин в образцах и элементах конструкций.
На основе использования свойств элементарного нестационарного случайного процесса (25) предлагается метод прогнозирования развития одной конкретной реализации, входящей в состав множества возможных физических реализаций данного случайного процесса. Для решения вопроса прогнозирования нужно знать детерминированную функцию ψ (t), входящую в уравнение (25).
Приведем один из возможных подходов к определению функции ψ (t). Как известно, скорость роста усталостной трещины в листовнх образцах из алюминиевых и титановых сплавов достаточно хорошо описывается уравнением Париса
(26)
где t - полудлина трещины; m - показатель, зависящий от материала.
Размах коэффициента интенсивности напряжений определяем по формуле
(27)
Где 
; F(t) - поправочный множитель, зависящий
от геометрии образца; 
(2b - характерный размер образца).
Подставляя формулу (27) в уравнение (26), после соответствующих преобразований получаем (при ∆Ϭ=const):
(28)
где
(29)
Уравнение (28) превращаеться в уравнение (25), если
(30)
Уравнение (28) превращается в уравнение (25), воля
|
Таким образом, рассматриваемый процесс росла усталостной трещины приведен к уравнению (25), которое является характерным для элементарннх нестационарных случайных процессов. При этом попутно получено выражение (30) для определения детерминированной функция ψ(t). Зная функцию F(t) для данного образца или конструктивного элемента, можно по формуле (29) найти ψ(t,t0), следовательно, и ψ(t).
После определения функции ψ(t) можно возвратиться к вопросу
предсказания развития одной конкретной реализации случайного процесса (25). Если провести наблюдения за развитием конкретной реализации Xк на ранней стадии ее развития, то можно определить, какое значение Ак приняла случайная величина А применительно к данной реализация:
(31)
Наблюдение при t=t1 за данной реализацией позволяет определить величину Хк(t1). Тогда, подставляя в выражение (31) t1вместо t, находим
| Для большой точности можно провести наблюдения за данной реализацией не один раз, а несколько, а именно при t =t1,t2.... Тогда получим несколько значений: |
в этом случае
Эти наблюдения необходимо производить на ранней стадии, развития рассматриваемой реализации. Тогда эффект предсказания будет иметь практическое значение. После определения величины Ак дальнейшее развитие реализации будет определяться формулой (31), Следовательно, теоретически обоснована возможность прогнозирования роста усталостной трещины в конкретном экземпляре образца или конструктивного элемента.
Методические указания
Для овладения методами оценки остаточной прочности элементов авиаконструкций с трещинами надо сначала ознакомиться с понятиями I -интеграла и R -кривых, обратив внимание на практические способы построения графиков I - ∆ и R -кривых. Далее нужно изучить вопросы, связанные с практическим применением I -иптегрела и R -кривых для оценки прочности некоторых конкретных элементов авиационной техники при наличии в них трещин.
Для того чтобы овладеть методами оценки остаточной долговечности элементов конструкций с трещинами, нужно познакомиться с уравнениями, связывающими скорость роста усталостных трещин о коэффициентом интенсивности напряжений. Затем следует освоить технику интегрирования уравнений Париса, Формана и др. Желательно также обратить внимание на способ прогнозирования развитая усталостной трещины в данном экземпляре конструктивного элемента.
Литература: [3, с. 200-205]; [4, с. 112-128]; [6, с. 38-45]; [7, с. 142-165]; [12, с. 22-27].
Вопросы для самопроверки
1.Что такое I-интеграл? Как его можно вычислить?
2.В чем заключается метод R -кривых?
3.Поясните методику применения I -интеграла для описания разрушения вращающегося диска.
4.Как произвести расчет остаточной прочности с использованием R -кривых (на примере панели крыла самолета).
5.Что такое раскрытие в вершине трещины?
6.Какие существуют уравнения, связывающие скорость роста усталостной трещины с коэффициентом интенсивности напряжений?
7.Как произвести расчет на усталость с помощью методов механики разрушения?
8.Поясните основную идею прогнозирования развития усталосной трещины в данном экземпляре конструктивного элемента.
СПИСОК ЛИТЕРАТУРЫ
1.БОРОДАЧЕВ Н.М. О характере случайного процесса распространения усталостных трещин. - Проблемы прочности, 1980, № 8,
с. 49-51.
2.БОРОДАЧЕВ Н.М., ХОДАК Н.А. О прогнозировании скорости распространения усталостных трещин в образцах и тонкостенных конструктивных элементах с учетом некоторых их геометрических параметров. - В кн.: Трещяностойкость материалов и элементов конструкций: Всесоюз. симпозиум. Киев: Наук, думка, 1980, с. 288-294.
3.БРОЕК Д. Основы механики разрушения. - М.: Высш. шк., 1980. - 368 с.
4.ВАСИЛЬЧЕНКО Г.С., КОШЕЛЕЕ П.Ф. Практическое применение механики разрушения для оценки прочности конструкций. - М.: Наука, 1974. - 147 с.
5.МАХУТОВ Н.А. Сопротивление элементов конструкций хрупкому разрушению. - М.: Машиностроение, 1973. - 201 с.
6.МИКЛЯЕВ П.Г., НЕШПОР Г.С., КУДРЯШОВ В.Г. Кинетика разрушения. - М.: Металлургия, 1979. - 278 с.
7.НОТТ Дж. Ф. Основы механики разрушения. - М.: Металлургия, 1978. - 256 с.
8.ПАРТОН В.З., МОРОЗОВ Е.М. Механика упругопластического разрушения. - М.: Наука, 1985. - 502 с.
9.РОТВАНИ М.М., УИЛХЕМ Д.П. Использование кривых сопротивления разрушению для расчета остаточной прочности. - Теоретические основы инж. расчетов, 1978, № 2, с. 29-34.
10.ИСПОЛЬЗОВАНИЕ метода I -интеграла для описания разрушения вращающегося диска / М. Саката; С. Аоки, М. Канзава и др. - Теоретические основы инж, расчетов, 1978, № 2, с. 19-25
11. УЭЙ Р.П. Применение методов механик раврушения при проектировочных расчетах на усталость.— Теоретические основы инж.расчетов, 1978,№ 2, с. 1-9.
12.ХЛРДРАТ Г. Усталостная прочность и долговечность конструкций летательных аппаратов. - Экспресс-информация. Авиастроение /ВИНИТИ, 1971, № 5, С. 10-30.
13.ЧЕРЕПАНОВ Г.П. Механика хрупкого разрушения. - М.: Наука, 1974. - 640 с.
14.CARTWRIGHT D.I. Stress Intensity Factor Determination. –In: Developments in Fracture Mechanics, 1 – London: Applied Science Publishers. 1979, p29-6.
15.Rolf S.T., BARSOM I.M. Fracture and Fatigue Control in Strictures. – New Jersey: Prentice – Hall, 1977-562p.
Приложение
Плоская деформация в обобщенное плоское напряженное состояние
Все уравнения теории упругости значительно упрощаются в тех случаях, когда ее задачу можно свести к отысканию функций только двух переменных, например, X и Y.
В упругом теле возникает плоская деформация, если перемещения будут происходить только параллельно плоскости хОу:
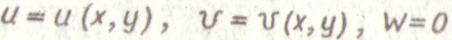
Такие перемещения возникают в длинном призматическом теле, ось которого параллельна оси z, при загружении его нагрузкой, перпендикулярное к оси z и постоянной вдоль этой оси. Близкими к этому случаю являются задачи о длинной подпорной стенке или плотине (рис.1.а), длинном цилиндрическом катке (вис.1.6) пли условии.
рис. 1(а,б)
что нагрузка не меняется вдоль оси z. В таких задачах деформации происходят только в плоскости хОу.В этом случае
Отсутствие линейных деформаций в направлении оси z ведет к появлению нормальных напряжений 
где ν -коэффщиент Пуассона.
При плоской деформации
В задаче о тонкой пластинке, загруженной по боковой поверхноcти силами, параллельными ее основаниям и равномерно распределеными по ее толщине (рис, 2), возможны также некоторые упрощения.
рис.2
В этом случае, который называется обобщенным плоским напряженным состоянием, на основаниях пластинки напряжения Ϭz, τ yzи τ xz равны нулю. Так как пластинка тонкая, то можно считать, что эти напряжения равны нулю и по всему объему пластинки. Остальные напряжения можно считать постоянными по толщине пластинки, т.е. не зависящими от z.. В тонкой пластинке, загруженной указанными силами, возникает приблизительно следующее напряженное состояние:
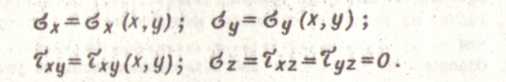
При решении задач о плоской деформации и обобщенном плоском напряженном состоянии можно пользоваться одними и теми же уравнениями и объединять обе задачи в одну: плоскую задачу теории упругости (разница имеется только в постоянных, входящих в уравнения).
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ 3
ГЛАВА I. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ РАЗРУШЕНИИ 3
1,1 Модель тела с трещинами 3
1,2 Виды деформаций в области кончика трещины 5
1,3 Поля напряжений и перемещений вблизи кончика трещины. Коэффициент интенсивности напряжений 6
1,4 Условие разрушения Ирвина 9
1,5 Определение коэффициентов интенсивности напряжений.... 9
1,6 Экспериментальное определение Кс и К1С 14
1,7 Практическое применение механики разрушения 18
ГЛАВА 2. ПРИМЕНЕНИЕ МЕХАНИКИ РАЗРУШЕНИЯ К ОЦЕНКЕ СОСТОЯНИЯ
ЭЛЕМЕНТОВ КОНСТРУКЦИЙ С ТРЕЩИНАМИ 21
2,1 Общие сведения 21
2,2 Метод I -интеграла 21
2.3 Метод R -кривых 25
2.4 Раскрытие в вершине трещины (СОD) 26
2.5 Использование метода I -интеграла для описании разрушения вращающегося диска....... 27
2.6 Расчет остаточной прочности с использованием кривых сопротивления разрушению (R -кривых) 28
2.7 Развитие усталостных трещин 30
2.8 Расчет на усталость с помощью методов механики разрушения 32
2.9 Обоснование возможности прогнозирования развитая усталостной трещины в данном экземпляре конструктивного элемента 35
СПИСОК ЛИТЕРАТУРЫ 40
Приложение. Плоская деформация в обобщенное плоское напряжен ное состояние.42
