Общие сведения
Для оценки остаточной прочности и долговечности элементов авиаконструкций при наличии в них трещин весьма эффективными оказались методы механики разрушения. При определении остаточной прочности применяют кривые сопротивления разрушению и метод I интеграла. Для оценки остаточной долговечности используют способ, основанный на интегрировании дифференциальных зависимостей, связывающих скорость роста усталостной трещины с коэффициентом интенсивности напряжен.
2,2Метод I -интеграла
Для оценки напряженно-деформированного состояния материала у вершины трещины Дж. Райс предложил использовать так называемый
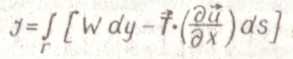 (15)
(15)
где Г - произвольный контур, окружающий вершину трещины (рио.17); начинающийся на нижней поверхности трещины и заканчивающийся на верхней поверхности; W - плотность энергии деформации;
T- вектор напряжения на площадке с внешней нормалью n; и - вектор перемещений; s ~ длина дуги вдоль Г.
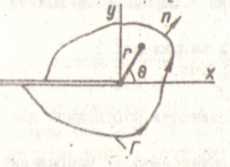 Разность I1- I2 для двух кривых Г1 и Г2. равна нулю, т.е. I -интеграл не зависит, от пути и формально эквивалентен изменению потенциальной энергии, когда длина надреза (трещины) увеличивается на
Разность I1- I2 для двух кривых Г1 и Г2. равна нулю, т.е. I -интеграл не зависит, от пути и формально эквивалентен изменению потенциальной энергии, когда длина надреза (трещины) увеличивается на 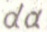 (рис. 18,а):
(рис. 18,а):
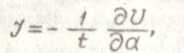 (16)
(16)
рис.17
где t- толщина образца; U- потенциальная энергия.
 Определение (16) схематически изображено на рис, 18,б, где заштрихованная область дU = It
Определение (16) схематически изображено на рис, 18,б, где заштрихованная область дU = It 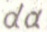 . Перемещение измеряется вдоль линии действия силы Р,
. Перемещение измеряется вдоль линии действия силы Р, 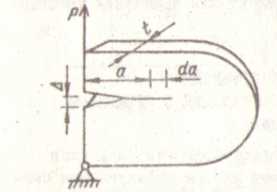 Рис 18.
Рис 18.
Параметр I был вначале введен для анализа нелинейного упругого поведения материала. Затем его стали использовать при анализе упругопластического поведения материала и условий общей текучести.
Если для упругого тела в качестве кривой Г ваять окружность радиуса Г и устремить Г→ О, то из выражения (15) следует, что вклад в I -интеграл дают только напряжения и деформации в окрестности кончика трещины.
В реальных телах, являющихся скорее упругопластичеcкими, чем нелинейно упругими, определение I осложняется. Рассмотрим случай, когда у вершины трещины существует область текучести, малая по сравнению с длиной трещины и шириной образца. Тогда I -интеграл можно оценить, выбрав Г -контур, проходящий через упругодеформированный материал, охватывающий пластическую зону.
Наиболее прямой экспериментальный метод определения, I -интеграла вытекает на его определения как изменения потенциальной энергии с длиной трещины,
При определенной длине трещины в случае линейной упругости зависимость I -интеграла от смещения ∆ имеет вид
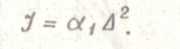
Для жесткопластического матерела
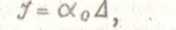
Где ɑ1 - ɑ0 коэффициенты.
В реальных материалах происходят переход от линейной упругости при низких нагрузках к полной пластичности при нагрузках, выэываюших общую текучесть.
На рис.19 показано изменение I -интеграла в зависимости от смещения ∆: вначале зависимость параболическая, затем переходная область (штриховая линяя) и потом линейная.
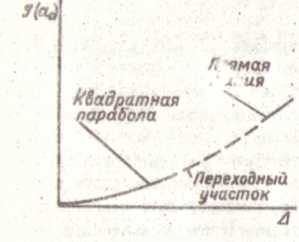 рис.19
рис.19
Для данного образца I -интеграл можно оценить либо экспериментальным, либо расчетным путем.
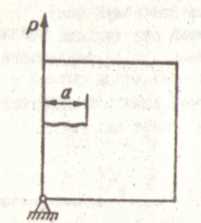
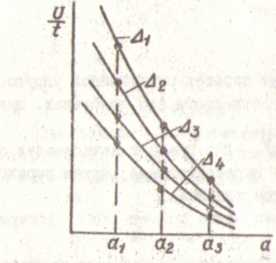
Для краткого описания процедуры вычисления I -интеграла как функции перемещения ∆ при использовании экспериментального метода выберем образец для испытаний (рис. 20,а), причем нужно иметь несколько экземпляров отличавшихся друг от друга только длиной трещины а. На основании испытаний образцов построим кривые Р- ∆. Для каждого образца о начальной длиной трещины ɑi (i = 1,2,3,...,n) построим свою кривую Р - ∆ (рис. 20,б). Для каждой величины перемещения А площадь под кривой Р- ∆ может рассматриваться как псевдопотенциальная энергия тела при этом перемещении. Эту энергию U, деленную на толщину образца t, откладываем как Функцию длины трещины ɑ при различных значениях ∆ (рис. 20,в). Используя далее формулу (16) и применяя численное дифференцирование, получаем кривые I -а для различных ∆.
 а)
а) 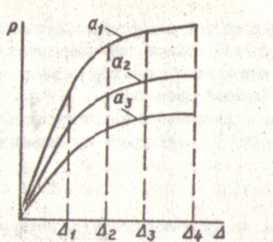 б)
б)
в)  г)
г)
рис. 20
Эти кривые можно затем перестроить в графики I- ∆ для различных значений длины трещины ɑ (рис. 20,г).
Введем понятие о критической величине I -интеграла I1c, представляющей критерий разрушения в случаях, когда разрушению предшествует развитая деформация материала.
Эксперименты, в которых измеряли значение I -интеграла при разрушении образцов двух различных геометрий, позволили получить два различающихся напряженных состояния, показывающих, что в обоих случаях разрушение характеризуется одним и тем же значением I 1c
При исследовании толстого образца с центральной трещиной на растяжение и на изгиб с длинной трещиной в качестве испытуемого материала была выбрана легированная сталь средней прочности (Ϭт ≈900 МПа). Значения I -интеграла определяли экспериментальным путем. Для смещений, соответствующих началу разрушения, были измерены значения I 1с, которые оказались достаточно постоянными.
Это свидетельствует о том, что параметр I1С достаточно полно характеризует разрушение образцов различной геометрии (в данном случае I ≈ 180 кДж/м2).
Метод R -кривых
Критическим коэффициентом интенсивности напряжений в условиях плоской деформации, когда пластическая зона у вершины трещины мала, является К1с,а критическим коэффициентом интенсивности напряжений при плоском напряженном состоянии, когда пластическая область у кончика трещины большая, -Кс. Обычно Кс в 2-10 раз больше К1с ; и зависит от толщины образца t и начальной длины трещины ɑ0. На практике случай плоского напряженного состояния встречается более часто, чем случай плоской деформации. Поэтому весьма актуальными являются попытки распространения механики упруголинейного разрушения на механику упругопластического разрушения. Метод R -кривых является одним из возможных подходов к исследованию упругопластического разрушения.R –кривых характеризуют сопротивление разрушению материалов в процессе медленного стабильного роста трещины и представляют собой графики изменения вязкости, когда трещина движется устойчиво под действием возрастающей нагрузки.
Примечание.R-кривые зависят от толщины образца, температуры, скорости нагружения. R-кривая выражает зависимость сопротивления росту трещины в материале от действительного или эффективного увеличения длины трещины, КR - сопротивление росту трещин выраженное в единицах, соответствующих К, а именно в МН/м3/2. Кс~ взкость разрушения при плоском напряженном состояний равная по величине Ко в момент перехода к нестабильному росту трещины.
Штриховыми линиями на рис. 21 изображены зависимости К1 от длины трещины ɑ для постоянных нагрузок Р1, Р 2 или Р3, где Р3 >Р 2 > Р1. Сплошные линии показывают увеличение КR с увеличением нагрузки и увеличением длины трещины для двух различных начальных длин трещин ɑ0. Действительное увеличение длины трещины обозначено ∆ɑд. Две точки касания (рис. 21), где КR = Кс для ɑ0 =ɑ1 и ɑ0 =а2 представляют собой точки нестабильности.
Для данного образца строится одна R -кривая в координатах КR-∆ɑд. Затем эту кривую можно двигать вдоль оси абсцисс и давать ей положения, соответствующие различным
начальным длинам трещин (рис. 21). Для данного образца и условий испытаний Кс представляет особую точку на R -кривой.R -кривая описывает полное изменение величины К с в зависимости от начальной длины трещины ɑ0. Таким образом, олиа R-кривая весьма эффективно характеризует сопротивление материала разрушению и эквивалентна 10...15 непосредственным испытаниям при определении Кс при различных значениях ɑ0.
 рис.21
рис.21
Следовательно,R -кривая является достаточно общей характеристикой поведения разрушения в условиях плоского напряженного cостояния.






